Geodetska kupola (eng. geodesic dome) je laka, ali jaka konstrukcija koja se sastoji od trougličaste mreže raspoređene po sferi. Njenu popularnost je u 20. veku proširio R. Buckminster Fuller, a koristi se u arhitekturi, plastenicima, paviljonima, pa i u futurističkim projektima (npr. Mars habovi).
Ona se zasniva na pretvaranju sfere u mrežu trouglova, što joj daje:
- visoku čvrstoću (dobro raspoređeno opterećenje),
- laku strukturu (može se graditi od tankih šipki),
- efikasno pokrivanje prostora sa malo materijala.
Šta znači frekvencija (npr. 2V, 3V, 5V)?
“V” znači “frequency” – frekvencija podele ikosaedra.
Geodetska kupola najčešće nastaje podelom lica ikosaedra (telo sa 20 jednakostraničnih trouglova) u više manjih trouglova.
- 1V – svaka ivica ikosaedra je nepodeljena (osnovna forma).
- 2V – svaka ivica se deli na 2 dela, pa nastaje više trouglova.
- 3V – deli se na 3 dela, još više trouglova.
- …
- 5V – veoma detaljna mreža, mnogo trouglova, glađa sfera.
2V
3V
4V
5V

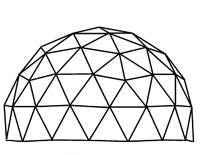
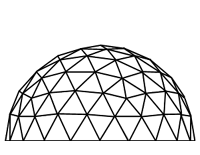

Što je veća frekvencija, kupola je:
- glađa (bliže savršenoj polulopti),
- složenija za izradu,
- bolje podnosi opterećenje,
- ali i zahteva više različitih dužina šipki.
Tipovi geodetske kupole (po visini preseka sfere):
Kupola je samo deo sfere. Možemo seći sferu na različitim visinama:
| Tip kupole | Opis | Ugao osnove | Visina u odnosu na poluprečnik |
|---|---|---|---|
| 5/8 | Kupola pokriva 5/8 sfere | Oko 144° | Visoka kupola |
| 3/8 | Kupola pokriva 3/8 sfere | Oko 67.5° | Pljosnatija, šira |
| 1/2 | Klasična hemisfera | 90° | Pola sfere |
| Pun | Cela sfera | 180° | Zatvorena kugla |
Za gradnju kuće ili plastenika, često se koristi 3/8 ili 5/8 kupola:
- 3/8 je stabilnija i ima niži centar gravitacije – pogodna za vetrovite krajeve.
- 5/8 daje veći unutrašnji prostor, bolja za stajanje i ventilaciju.
Ukratko:
- Geodetska kupola je čvrsta konstrukcija od trouglova raspoređenih po sferi.
- Frekvencija (npr. 3V, 5V) određuje koliko je kupola detaljna i “glatka”.
- Tip kupole (3/8, 5/8, 1/2) određuje koliko “visoko” sečeš sferu — i time oblik.

Uporedo radim dve verzije programa. Prva verzija geo.py računski izvodi strut faktore iz projekcije ikosaedra na sferu, i iz podele trouglova . Druga verzija programa je geosf.py koristi tabelu strut faktora za određeni tip kupole i frekvenciju (postoje gotove vrednosti za svaku kombinaciju) i radi tačno tako da tačnost prve verzije proveravam drugom verzijom.
Pojam “strut factor” se najčešće koristi u kontekstu geodetskih kupola (ali i kod drugih mrežastih struktura), kada želiš da izračunaš pravu (realnu) dužinu šipki (struts) koje grade konstrukciju. Hajde da to lepo pojasnim:
🧱 Šta je strut?
U konstrukciji kupole:
- Strut (šipka) je element koji povezuje dva čvora (tačke).
- Geodetska kupola je sastavljena od mreže trouglova, a stranice tih trouglova su struts.
📏 Šta je strut factor?
Strut factor je broj koji koristiš da:
- pretvoriš dimenziju jedinice na sferi u realnu dužinu šipke.
To je skalar koji množiš sa poluprečnikom kupole (ili sa jedinicom ako je kupola normirana), kako bi dobio dužinu određene klase šipki.
🧮 Formula:
Ako imaš kupolu sa poluprečnikom R, i znaš strut factor za određenu šipku, onda je:
Dužina šipke (strut) = strut factor x R
Na primer:
- Ako R = 100 cm (poluprečnik kupole)
- A strut factor za neku klasu šipke je 0.856
- Onda je dužina šipke:
0.856×100=85.6 cm
📊 Gde se koriste strut faktori?
Kod viših frekvencija (npr. 3V, 4V, 5V…) šipke nisu sve iste dužine. Po pravilu:
- Ima više klasa dužina šipki, npr. A, B, C…
- Svaka klasa ima svoj strut factor
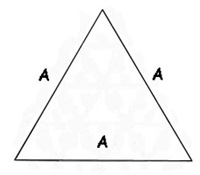
Primer za 3V 5/8 kupolu:
| Klasa | Strut factor | Dužina za R = 100 cm |
|---|---|---|
| A | 0.618 | 61.8 cm |
| B | 0.715 | 71.5 cm |
| C | 0.755 | 75.5 cm |
🛠️ Kako se dobijaju ti faktori?
Obično se:
- računski izvode iz projekcije ikosaedra na sferu, i iz podele trouglova,
- ili preuzimaju iz tabela za određeni tip kupole i frekvenciju (postoje gotove vrednosti za svaku kombinaciju).
✅ Ukratko:
- Strut factor = koeficijent koji ti kaže koliko je određena šipka dugačka u odnosu na poluprečnik kupole.
- Koristiš ga da izračunaš tačne dužine šipki za sečenje i montažu.
- Svaka klasa šipki (A, B, C…) ima svoj strut factor.
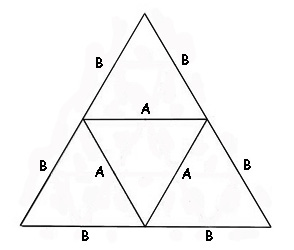
| Strut | Strut factor | Dome | Sphere |
 |
| A | 1.05146 | 25 | 30 | |
| 5-way connectors | 6 | 12 | ||
| 4-way connectors | 5 | 0 | ||
| Strut | Strut factor | Dome | Sphere |
 |
| A | .61803 | 35 | 60 | |
| B | .54653 | 30 | 60 | |
| 4-way connectors | 10 | 0 | ||
| 5-way connectors | 6 | 12 | ||
| 6-way connectors | 10 | 30 | ||
| Strut | Strut factor | 3/8 | 5/8 | Sphere |
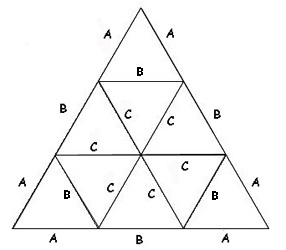 |
| A | .34862 | 30 | 30 | 60 | |
| B | .40355 | 40 | 55 | 90 | |
| C | .41241 | 50 | 80 | 120 | |
| 4-way connectors | 15 | 15 | 0 | ||
| 5-way connectors | 6 | 6 | 12 | ||
| 6-way connectors | 25 | 40 | 80 | ||
| Strut | Strut factor | Dome | Sphere |
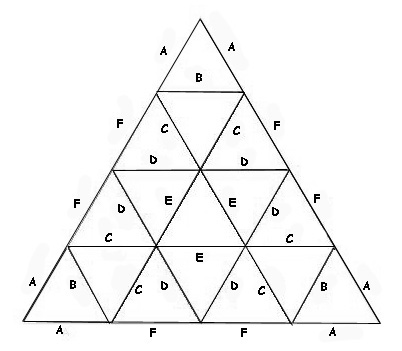 |
| A | .25318 | 30 | 60 | |
| B | .29524 | 30 | 60 | |
| C | .29453 | 60 | 120 | |
| D | .31287 | 70 | 120 | |
| E | .32492 | 30 | 60 | |
| F | .29859 | 30 | 60 | |
| 4-way connectors | 20 | 0 | ||
| 5-way connectors | 6 | 12 | ||
| 6-way connectors | 65 | 150 | ||
| Strut | Strut Factor | Dome | Sphere |
 |
| A | .19814743 | 30 | 60 | |
| B | .23179025 | 30 | 60 | |
| C | .22568578 | 60 | 120 | |
| D | .24724291 | 60 | 120 | |
| E | .25516701 | 70 | 120 | |
| F | .24508578 | 80 | 120 | |
| G | .26159810 | 40 | 60 | |
| H | .23159760 | 30 | 60 | |
| I | .24534642 | 20 | 30 | |
| 4-way connectors | ?? | 0 | ||
| 5-way connectors | 6 | 12 | ||
| 6-way connectors | ?? | ?? | ||
| Strut | Strut Factor | Dome | Sphere |
 |
| A | .1625672 | 30 | 60 | |
| B | .1904769 | 30 | 60 | |
| C | .1819083 | 60 | 120 | |
| D | .2028197 | 90 | 180 | |
| E | .1873834 | 30 | 60 | |
| F | .1980126 | 60 | 120 | |
| G | .2059077 | 130 | 240 | |
| H | .2153537 | 65 | 120 | |
| I | .2166282 | 60 | 120 | |
| 4-way connectors | ?? | 0 | ||
| 5-way connectors | 6 | 12 | ||
| 6-way connectors | ?? | ?? | ||
Programi koje sam pravio za proračunavanje geodetske kupole:
Linkovi:
