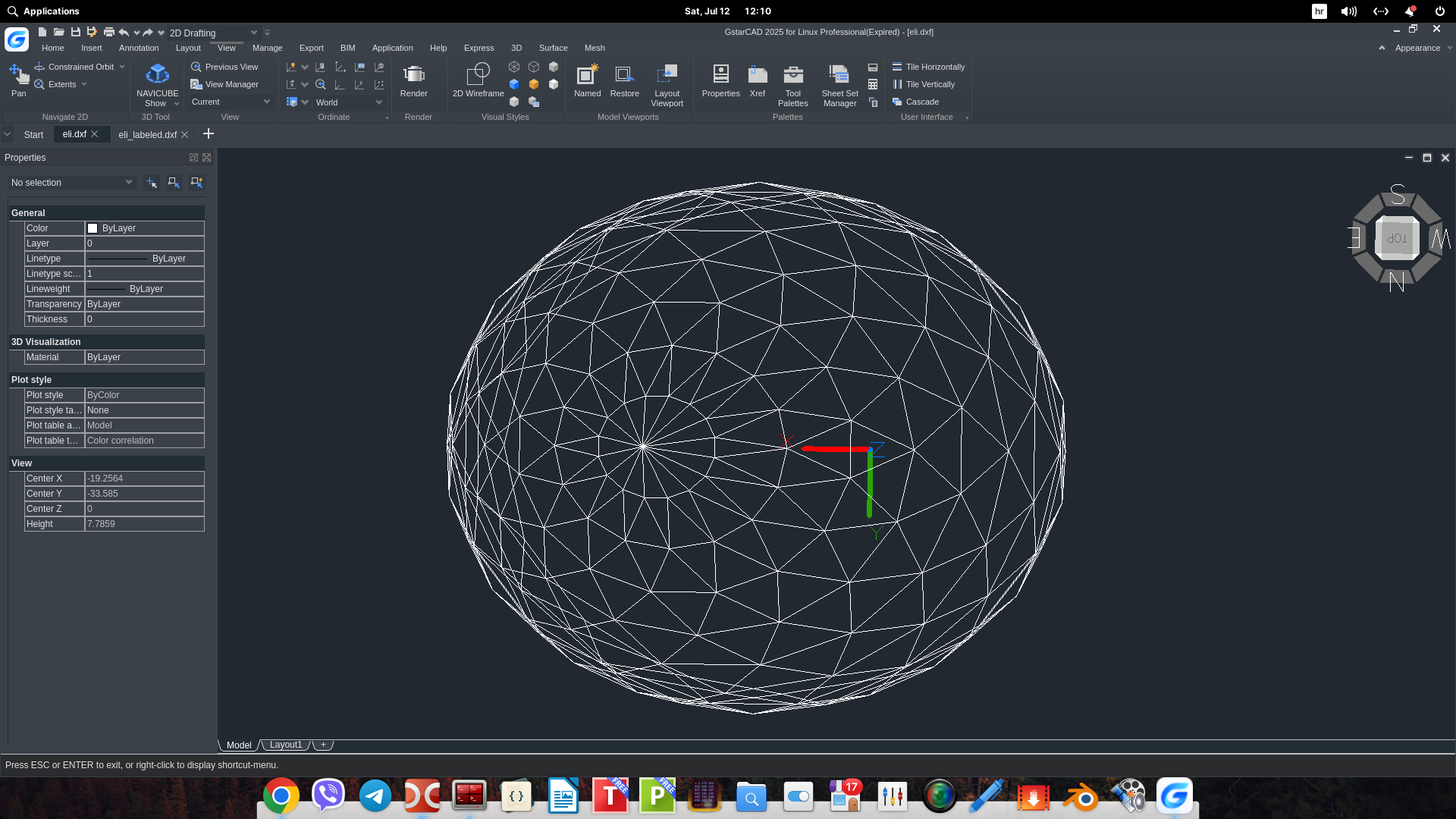
Spiralna zome kupola sa eliptičnom bazom predstavlja kompleksnu prostornu strukturu zasnovanu na ukrštanju dvostrukih spirala koje se uzdižu iz elipse ka vrhu kupole. Ova geometrija omogućava asimetričnost, jer se vrh može pomeriti van centra baze, čime se dobija dinamična i arhitektonski atraktivna forma. U nastavku je dat detaljan matematički opis takve kupole, uključujući parametarski model spirala, definiciju eliptične baze, algoritam presecanja i pravila konstrukcije mreže.
Matematički opis spiralne zome kupole sa eliptičnom bazom
Spiralna zome kupola zasnovana na eliptičnoj bazi formira se pomoću parametarskih spirala koje rastu iz baze prema vrhu kupole. Osnovna geometrija svake spirale određena je sledećim parametrima:
- \( a \) — horizontalna poluosa elipse
- \( b \) — vertikalna poluosa elipse
- \( h \) — visina kupole
- \( n \) — broj spirala (radijalna simetrija)
- \( \theta \) — ugao spirale (varira od 0 do \( \pi \))
- \( \beta \) — ugaona faza spirale: \( \beta = \frac{2\pi i}{n} \), gde je \( i \) indeks spirale
- \( \text{center}_x, \text{center}_y \) — pomak vrha kupole u odnosu na centar baze
1. Parametarski oblik spirale
Svaka spirala je definisana u prostoru kao niz tačaka \( (x, y, z) \) gde:
\[ \begin{aligned} \theta &= \alpha \quad \text{ili} \quad -\alpha \quad (\text{u zavisnosti od smera}) \\ \text{scale} &= \sin(\alpha) \\ x(\alpha) &= a \cdot \sin(\theta + \beta) \cdot \text{scale} + \frac{\text{center}_x \cdot \alpha}{\pi} \\ y(\alpha) &= b \cdot \cos(\theta + \beta) \cdot \text{scale} + \frac{\text{center}_y \cdot \alpha}{\pi} \\ z(\alpha) &= \frac{\alpha}{\pi} \cdot h \end{aligned} \] Za \( \alpha \in [0, \pi] \), spirala se proteže od baze ka vrhu.
2. Eliptična baza
Baza kupole je elipsa definisana u ravni \( z = 0 \) sa jednačinom:
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \] Pomak vrha kupole uveden je pomoću linearnog interpoliranog pomaka od centra elipse prema vrhu:
\[ \text{offset}_x = \frac{\text{center}_x \cdot \alpha}{\pi}, \quad \text{offset}_y = \frac{\text{center}_y \cdot \alpha}{\pi} \] Ovo omogućava asimetričnost kupole: vrh ne mora biti iznad centra baze.
3. Presecanje kupole po ravni
Kupola se može preseći horizontalnom ravni \( z = z_{\text{cut}} \), pri čemu se zadržavaju samo tačke koje zadovoljavaju:
\[ z(\alpha) \geq z_{\text{cut}} \quad \Rightarrow \quad \frac{\alpha}{\pi} \cdot h \geq z_{\text{cut}} \] što implicira: \[ \alpha \geq \frac{\pi \cdot z_{\text{cut}}}{h} \]
4. Intersekcija spirala
Kupola je formirana ukrštanjem spirala koje idu u suprotnim smerovima (“desne” i “leve”), a čvorišta se nalaze na mestima gde su njihove tačke blizu — definisano tolerancijom:
\[ \| \vec{r}_L – \vec{r}_R \|^2 < \varepsilon^2 \] Gde je \( \varepsilon \) zadati prag tolerancije (npr. 0.02).
5. Vizualna i strukturna mreža
Spojene tačke formiraju žičani model sa:
- vertikalnim linijama duž spirala (po dubini)
- horizontalnim linijama između susednih spirala (po širini)
Tako nastaje zome struktura, pogodna za dalju obradu, izvoz u 3D formate i konstrukciju u arhitektonskoj praksi.
Program helixAE.py
Za pokretanje programa potrebno je instalirati samo jednu biblioteku:
pip install numpy
Biblioteka math je ugrađena u Python i nije potrebna dodatna instalacija.
Pokretanje programa
Pokreni program komandnom linijom:
python3 helixAE.py
Bićeš redom upitan da uneseš sledeće parametre (možeš samo pritisnuti Enter da ostane podrazumevana vrednost):
Parametri programa
| Parametar | Objašnjenje | Primer vrednosti |
|---|---|---|
| Naziv izlaznog fajla | Ime .obj fajla za eksport | kupola.obj |
| Broj spirala (n) | Broj spirala u svakom smeru (CW i CCW) | 24 |
| Broj segmenata po spirali (segs) | Koliko delova ima svaka spirala | 24 |
| Visina kupole (h) | Visina strukture po z-osi | 3.0 |
| Poluosa a | Horizontalna poluosa elipse | 4.0 |
| Poluosa b | Vertikalna poluosa elipse | 2.0 |
| Pomak centra u X | Horizontalni pomak centra baze | 3.0 |
| Pomak centra u Y | Vertikalni pomak centra baze | 0.0 |
| Tolerancija preseka | Preciznost pri detekciji preseka spirala | 0.02 |
| Z ravnina preseka (z_cut) | Sve tačke ispod ove vrednosti biće odbačene | 1.0 |
Rezultat
Na osnovu unetih parametara program generiše asimetričnu spiralnu zome kupolu sa eliptičnom osnovom, i to tako da:
- Prvo generiše spirale u dva suprotna smera.
- Pronalazi njihove preseke.
- Filtrira preseke koji su iznad određene visine
z_cut. - Kreira žičani 3D model (.obj fajl) samo za presečeni gornji deo.
Fajl koji se dobija (.obj) možeš otvoriti u 3D alatima kao što su Blender, MeshLab, Rhino ili ArchiCAD (preko Add Object).
Programski kod za helixAE.py
#helixAE.py
# The MIT License (MIT)
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovim se omogućava bilo kome da koristi, kopira, menja, spaja, objavljuje,
# distribuira, daje podlicencu i/ili prodaje kopije ovog softverskog programa,
# uz uslov da u svim kopijama ili značajnim delovima softverskog programa bude
# uključena sledeća obavest:
#
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovaj softverski program je pružen "takav kakav jeste", bez bilo kakvih garancija,
# izričitih ili impliciranih, uključujući, ali ne ograničavajući se na, garancije o
# prikladnosti za prodaju ili pogodnosti za određenu svrhu. U svakom slučaju, autori
# ili nosioci prava nisu odgovorni za bilo kakvu štetu ili druge obaveze koje mogu nastati
# usled upotrebe ovog softverskog programa.
# Naziv programa: Generator spiralne asimetrične helix zome kupole sa eliptičnom bazom i presecanjem po z
# instalacija potrebnih zavisnosti: pip install numpy
import numpy as np
from math import sin, cos, pi
def input_with_default(prompt, default, type_func=float):
user_input = input(f"{prompt} [{default}]: ").strip()
if user_input == '':
return default
try:
return type_func(user_input)
except ValueError:
print(" Neispravan unos, koristi se podrazumevana vrednost.")
return default
def generate_spiral_ellipse(n, segs, a, b, h, direction, center_offset=np.array([0.0, 0.0])):
spirals = []
for i in range(n):
beta = 2 * pi * i / n
spiral = []
for j in range(segs + 1):
alpha = pi * j / segs
theta = alpha if direction == 1 else -alpha
scale = sin(alpha)
offset_x = center_offset[0] * (alpha / pi)
offset_y = center_offset[1] * (alpha / pi)
x = a * sin(theta + beta) * scale + offset_x
y = b * cos(theta + beta) * scale + offset_y
z = (alpha / pi) * h
spiral.append([x, y, z])
spirals.append(np.array(spiral))
return spirals
def find_intersections(spirals_right, spirals_left, tol=1e-2):
intersections = []
index_map = {}
tol2 = tol * tol
right_points = []
right_map = []
for si, spiral in enumerate(spirals_right):
for pi, p in enumerate(spiral):
right_points.append(p)
right_map.append((si, pi))
right_points = np.array(right_points)
global_idx = 0
for si_left, spiral_left in enumerate(spirals_left):
for pi_left, p_left in enumerate(spiral_left):
diffs = right_points - p_left
dists2 = np.sum(diffs**2, axis=1)
close_indices = np.where(dists2 < tol2)[0]
if len(close_indices) > 0:
key_left = ('L', si_left, pi_left)
if key_left not in index_map:
index_map[key_left] = global_idx
intersections.append(p_left)
global_idx += 1
for ci in close_indices:
si_right, pi_right = right_map[ci]
key_right = ('R', si_right, pi_right)
if key_right not in index_map:
index_map[key_right] = global_idx
intersections.append(right_points[ci])
global_idx += 1
intersections = np.array(intersections)
return intersections, index_map
def generate_wireframe_from_intersections_cut(filename, spirals_right, spirals_left, index_map, z_cut=0.0):
lines = []
# Prikupi sve tačke
global_points = [None] * (max(index_map.values()) + 1)
for key, idx in index_map.items():
side, si, pi = key
p = spirals_right[si][pi] if side == 'R' else spirals_left[si][pi]
global_points[idx] = p
# Filtriraj tačke koje su iznad ili na ravni z_cut
valid_points = {}
valid_index = 0
for i, p in enumerate(global_points):
if p[2] >= z_cut:
valid_points[i] = valid_index
valid_index += 1
# Poveži linije duž spirala samo za validne tačke
def connect_intersections(side, spirals):
for si, spiral in enumerate(spirals):
intersect_indices = []
for pi in range(len(spiral)):
key = (side, si, pi)
if key in index_map:
idx_orig = index_map[key]
if idx_orig in valid_points:
intersect_indices.append(valid_points[idx_orig])
for i in range(len(intersect_indices) - 1):
lines.append((intersect_indices[i] + 1, intersect_indices[i + 1] + 1))
connect_intersections('R', spirals_right)
connect_intersections('L', spirals_left)
# Poveži horizontalne linije između spirala, filtrirano po validnim tačkama
def connect_horizontal_lines():
for side, spirals in [('R', spirals_right), ('L', spirals_left)]:
n = len(spirals)
segs = len(spirals[0])
for pi in range(segs):
for si in range(n):
si_next = (si + 1) % n
key1 = (side, si, pi)
key2 = (side, si_next, pi)
if key1 in index_map and key2 in index_map:
idx1 = index_map[key1]
idx2 = index_map[key2]
if idx1 in valid_points and idx2 in valid_points:
lines.append((valid_points[idx1] + 1, valid_points[idx2] + 1))
connect_horizontal_lines()
# Upis u .obj fajl
with open(filename, 'w') as f:
for i in range(len(global_points)):
if i in valid_points:
p = global_points[i]
f.write(f"v {p[0]} {p[1]} {p[2]}\n")
for line in lines:
f.write(f"l {line[0]} {line[1]}\n")
print(f"\n Izvezen presečeni wireframe model u '{filename}' sa presekom na z >= {z_cut}")
# ---------------- MAIN ----------------
if __name__ == "__main__":
print(" Parametri za eliptičnu bazu kupole (Enter za podrazumevane vrednosti)\n")
filename = input("Naziv izlaznog fajla [.obj] [helix_zome_ellipse.obj]: ").strip()
if filename == "":
filename = "helix_zome_ellipse.obj"
elif not filename.endswith(".obj"):
filename += ".obj"
n = input_with_default("Broj spirala (n)", 24, int)
segs = input_with_default("Broj segmenata po spirali (segs)", 24, int)
h = input_with_default("Visina kupole (h)", 3.0)
a = input_with_default("Poluosa a (horizontalna)", 4.0)
b = input_with_default("Poluosa b (vertikalna)", 2.0)
offset_x = input_with_default("Pomak centra u X pravcu", 3.0)
offset_y = input_with_default("Pomak centra u Y pravcu", 0.0)
tol = input_with_default("Tolerancija preseka", 0.02)
center_offset = np.array([offset_x, offset_y])
z_cut = input_with_default("Z ravnina preseka (z_cut) [0.0]", 0.0)
spirals_right = generate_spiral_ellipse(n, segs, a, b, h, direction=1, center_offset=center_offset)
spirals_left = generate_spiral_ellipse(n, segs, a, b, h, direction=-1, center_offset=center_offset)
intersections, index_map = find_intersections(spirals_right, spirals_left, tol=tol)
generate_wireframe_from_intersections_cut(filename, spirals_right, spirals_left, index_map, z_cut=z_cut)
Linkovi:
https://abel.rs/kada-kupola-izgubi-ravnotezu-istrazivanje-asimetricne-zome-forme/