geox.py sračunava dimenzije i količinu trouglova potrebnih za izgradnju Geodetske kupole

Detaljno objašnjenje Šta je Geodetska Kupola i kako se izračunava?

Ovaj članak je moj podsetnik za izradu programa.

Šta je urađeno a šta tek treba uraditi:

Traži od korisnika prečnik sfere i frekvenciju mreže (stepen podele) os 1V do 5V

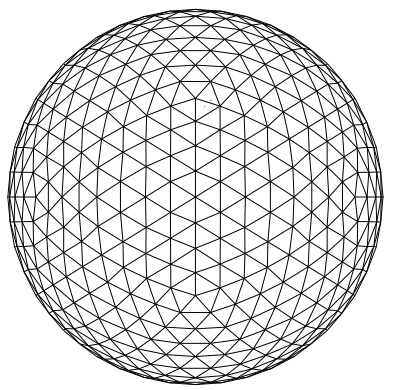
Pravi geodetsku kupolu (gornju polovinu sfere) od trouglova

Skalira sve tačke prema datom prečniku

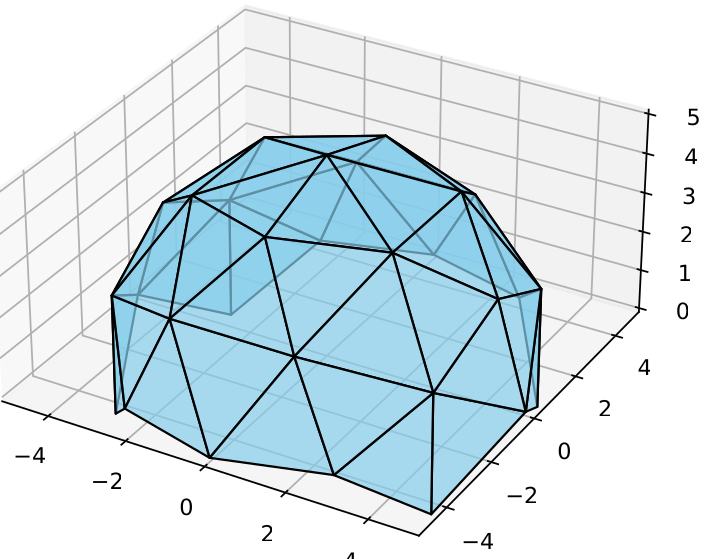
Vizuelno prikazuje kupolu

Automatski klasifikuje trouglove po tipu (prema dužinama stranica)

Prikazuje broj svake vrste trougla

Prikazuje broj letvica po dužini (sa tolerancijom) – spremno za gradnju!

Program automatski formira sledeće fajlove:

STL (StereoLithography) je jedan od najpopularnijih formata za 3D štampanje i prikazivanje 3D modela. Razvijen je za potrebe 3D štampača, ali se koristi i u mnogim 3D aplikacijama, posebno za prenos modela koji treba da se štampaju. STL fajl opisuje samo spoljašnju geometriju objekta, odnosno njegovu površinu, bez dodatnih informacija kao što su boje, materijali ili teksture.

SVG (Scalable Vector Graphics) je vektorski format za grafiku koji koristi XML (Extensible Markup Language) za opisivanje dvodimenzionalnih vektorskih slika. Ovaj format omogućava da slike budu skalabilne, što znači da se mogu uvećavati ili smanjivati bez gubitka kvaliteta, što je velika prednost u poređenju sa rasterizovanim formatima poput JPG ili PNG.

DXF (Drawing Exchange Format) je vektorski format za razmenu crteža koji je razvio Autodesk. Koristi se za razmenu podataka između različitih CAD (Computer-Aided Design) softverskih alata i omogućava prenos crteža i modela između različitih aplikacija koje se bave dizajnom, arhitekturom, inženjeringom i sličnim oblastima. DXF fajlovi mogu sadržavati različite vrste podataka, uključujući linije, krive, tekst, krugove, dimenzije i druge elemente koji se koriste u tehničkim crtežima.

CSV za Excel gde se nalazi spisak broj i dužina letvica

U planu je dogradnja programa za izvoz podataka u:

IFC (Industry Foundation Classes) je otvoreni format za BIM (Building Information Modeling). Njegova glavna svrha je da omogući razmenu podataka između različitih BIM softvera – npr. između ArchiCAD-a, Revit-a, Allplan-a, SketchUp-a i drugih.

OBJ format je popularan format za 3D modele koji se koristi za razmenu podataka između različitih 3D aplikacija. To je tekstualni format koji opisuje geometriju 3D objekta, uključujući njegove tačke (vertice), ivice, površine (facete), normalne vektore i koordinate tekstura. Obj format je jednostavan, prenosiv i kompatibilan sa mnogim 3D alatima.

JSON (JavaScript Object Notation) je lagan format za razmenu podataka koji koristi čitljiv tekst za predstavljanje struktura podataka kao što su objekti i nizovi. JSON je postao vrlo popularan zbog svoje jednostavnosti i fleksibilnosti, te se koristi u mnogim aplikacijama i web servisima za prenos podataka između servera i klijenata.

.xlsx za Excel tabelu lista trouglova i letvica

.pdf pregled 3D prikaza kao slika

PROGRAM JE U FAZI IZRADE I ISPITIVANJA TAKO DA REZULTATI NISU POUZDANI

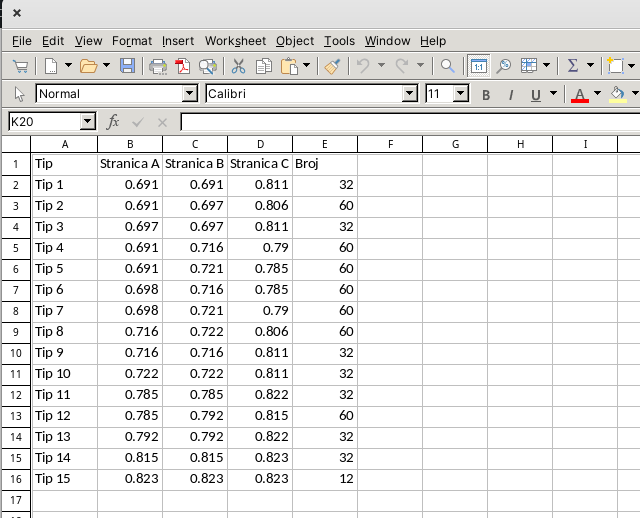
Prva verzija geox.py računski izvodi strut faktore iz projekcije ikosaedra na sferu, i iz podele trouglova. Sračunava tip i broj trouglova potrebnih za gradnju kupole i dužinu i broj letvica za izradu trouglova. Generiše DXF sa tlocrtom kupole, STL 3D model, Excel XLSX sa spiskom tipova trouglova, njihovim dimenzijama i brojem potrebnim za ugradnju. Program je pravljen zbog ideje da se kupola gradi od gotovih trouglova. Program je u fazi testiranja i dorade tako da još nije spreman za ozbiljnu upotrebu.

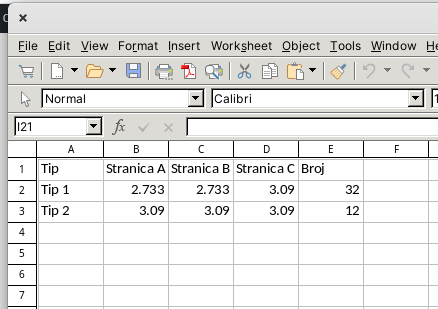
Druga verzija programa je geosf.py koristi tabelu strut faktora za određeni tip kupole i frekvenciju (postoje gotove vrednosti za svaku kombinaciju) i radi tačno tako da tačnost prve verzije proveravam drugom verzijom.

Instalacija potrebnih biblioteka:

pip3 install numpy pandas matplotlib openpyxl trimesh svgwrite ezdxf

geox.py

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
from collections import defaultdict
import svgwrite
import trimesh
import openpyxl
from openpyxl import Workbook
from datetime import datetime
import os
import ezdxf
from matplotlib.backends.backend_pdf import PdfPages

def normalize(v):
    norm = np.linalg.norm(v)
    return v / norm if norm > 0 else v

def midpoint(a, b):
    return (a + b) / 2

def project_to_sphere(point, radius):
    return normalize(point) * radius

def create_icosahedron():
    phi = (1 + np.sqrt(5)) / 2
    points = [
        (-1,  phi, 0), (1,  phi, 0), (-1, -phi, 0), (1, -phi, 0),
        (0, -1,  phi), (0, 1,  phi), (0, -1, -phi), (0, 1, -phi),
        (phi, 0, -1), (phi, 0, 1), (-phi, 0, -1), (-phi, 0, 1)
    ]
    vertices = np.array([normalize(np.array(p)) for p in points])

    faces = [
        [0, 11, 5], [0, 5, 1], [0, 1, 7], [0, 7,10], [0,10,11],
        [1, 5, 9], [5,11,4], [11,10,2], [10,7,6], [7,1,8],
        [3,9,4], [3,4,2], [3,2,6], [3,6,8], [3,8,9],
        [4,9,5], [2,4,11], [6,2,10], [8,6,7], [9,8,1]
    ]
    return vertices, faces

def subdivide_triangle(v1, v2, v3, depth):
    if depth == 0:
        return [(v1, v2, v3)]
    else:
        a = midpoint(v1, v2)
        b = midpoint(v2, v3)
        c = midpoint(v3, v1)
        return (
            subdivide_triangle(v1, a, c, depth - 1) +
            subdivide_triangle(a, v2, b, depth - 1) +
            subdivide_triangle(c, b, v3, depth - 1) +
            subdivide_triangle(a, b, c, depth - 1)
        )

def generate_geodesic_dome(freq=2, precnik=2.0):
    radius = precnik / 2.0
    vertices, faces = create_icosahedron()
    dome_faces = []

    for face in faces:
        v1, v2, v3 = vertices[face]
        subdivided = subdivide_triangle(v1, v2, v3, freq)
        for tri in subdivided:
            z_avg = sum([p[2] for p in tri]) / 3
            if z_avg >= 0:
                projected = [project_to_sphere(p, radius) for p in tri]
                dome_faces.append(projected)

    return dome_faces

def classify_triangles(faces, tolerance=1e-4):
    triangle_types = defaultdict(int)
    strut_lengths = defaultdict(int)

    for tri in faces:
        a, b, c = tri
        d1 = np.linalg.norm(a - b)
        d2 = np.linalg.norm(b - c)
        d3 = np.linalg.norm(c - a)
        edges = sorted([d1, d2, d3])
        key = tuple(round(e / tolerance) * tolerance for e in edges)
        triangle_types[key] += 1
        for d in key:
            strut_lengths[d] += 1

    return triangle_types, strut_lengths

def plot_geodesic_dome(faces, precnik, save_pdf=None):
    fig = plt.figure()
    ax = fig.add_subplot(111, projection='3d')
    poly3d = Poly3DCollection(faces, edgecolor='k', facecolor='skyblue', alpha=0.7)
    ax.add_collection3d(poly3d)
    r = precnik / 2
    ax.set_box_aspect([1, 1, 0.5])
    ax.set_xlim([-r, r])
    ax.set_ylim([-r, r])
    ax.set_zlim([0, r])
    ax.set_title(f"Geodetska kupola (prečnik {precnik} m)")
    plt.tight_layout()
    if save_pdf:
        with PdfPages(save_pdf) as pdf:
            pdf.savefig(fig)
    plt.show()

def export_stl(faces, filename):
    mesh = trimesh.Trimesh(vertices=[], faces=[])
    for tri in faces:
        mesh = mesh + trimesh.Trimesh(vertices=tri, faces=[[0, 1, 2]])
    mesh.export(filename)

def export_svg(faces, filename):
    dwg = svgwrite.Drawing(filename, profile='tiny')
    scale = 100
    offset = 200
    for tri in faces:
        pts = [(p[0] * scale + offset, -p[1] * scale + offset) for p in tri]
        dwg.add(dwg.polygon(pts, fill='white', stroke='black'))
    dwg.save()

def export_dxf(faces, filename):
    doc = ezdxf.new()
    msp = doc.modelspace()
    for tri in faces:
        pts = [(p[0]*100, p[1]*100) for p in tri]
        msp.add_lwpolyline(pts + [pts[0]], close=True)
    doc.saveas(filename)

def export_excel(triangle_types, strut_lengths, filename):
    wb = Workbook()
    ws1 = wb.active
    ws1.title = "Trouglovi"
    ws1.append(["Tip", "Stranica A", "Stranica B", "Stranica C", "Broj"])
    for i, (k, v) in enumerate(triangle_types.items(), 1):
        ws1.append([f"Tip {i}", *[round(x, 3) for x in k], v])
    ws2 = wb.create_sheet(title="Letvice")
    ws2.append(["Duzina (m)", "Kolicina"])
    for k, v in sorted(strut_lengths.items()):
        ws2.append([round(k, 3), v])
    wb.save(filename)

def main():
    try:
        precnik = float(input("Unesi prečnik sfere (npr. 10.0): "))
        frekvencija = int(input("Unesi frekvenciju (npr. 2 za 2V): "))-1
        
    except ValueError:
        print("Greška: Unos mora biti broj.")
        return

    dome_faces = generate_geodesic_dome(freq=frekvencija, precnik=precnik)

    now = datetime.now().strftime("%Y%m%d_%H%M")
    base_name = f"kupola_D{precnik}_F{frekvencija}_{now}"
    os.makedirs("izlaz", exist_ok=True)

    plot_geodesic_dome(dome_faces, precnik, save_pdf=f"izlaz/{base_name}.pdf")

    triangle_types, strut_lengths = classify_triangles(dome_faces)

    print("\nTipovi trouglova:")
    for i, (key, count) in enumerate(triangle_types.items(), 1):
        print(f"  Tip {i}: {count} kom → stranice ≈ {key[0]:.3f}, {key[1]:.3f}, {key[2]:.3f} m")

    print("\n Broj letvica po dužini:")
    for length, count in sorted(strut_lengths.items()):
        print(f"  {length:.3f} m: {count} kom")

    export_stl(dome_faces, f"izlaz/{base_name}.stl")
    export_svg(dome_faces, f"izlaz/{base_name}.svg")
    export_dxf(dome_faces, f"izlaz/{base_name}.dxf")
    export_excel(triangle_types, strut_lengths, f"izlaz/{base_name}.xlsx")

    print(f"\n Eksportovano u 'izlaz/{base_name}.[stl/svg/dxf/pdf/xlsx]'")

if __name__ == "__main__":
    main()

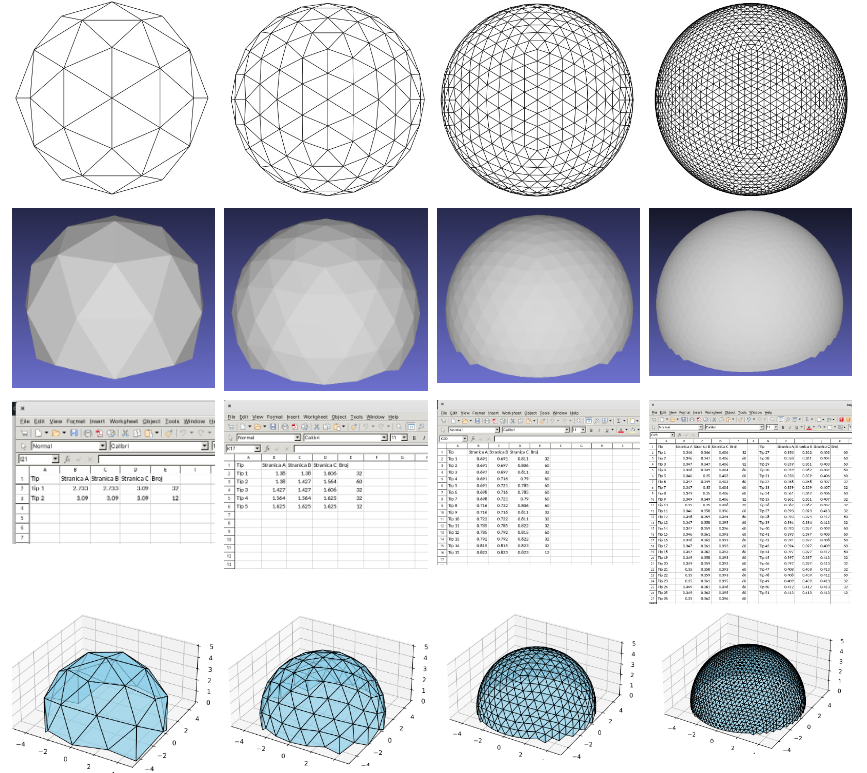
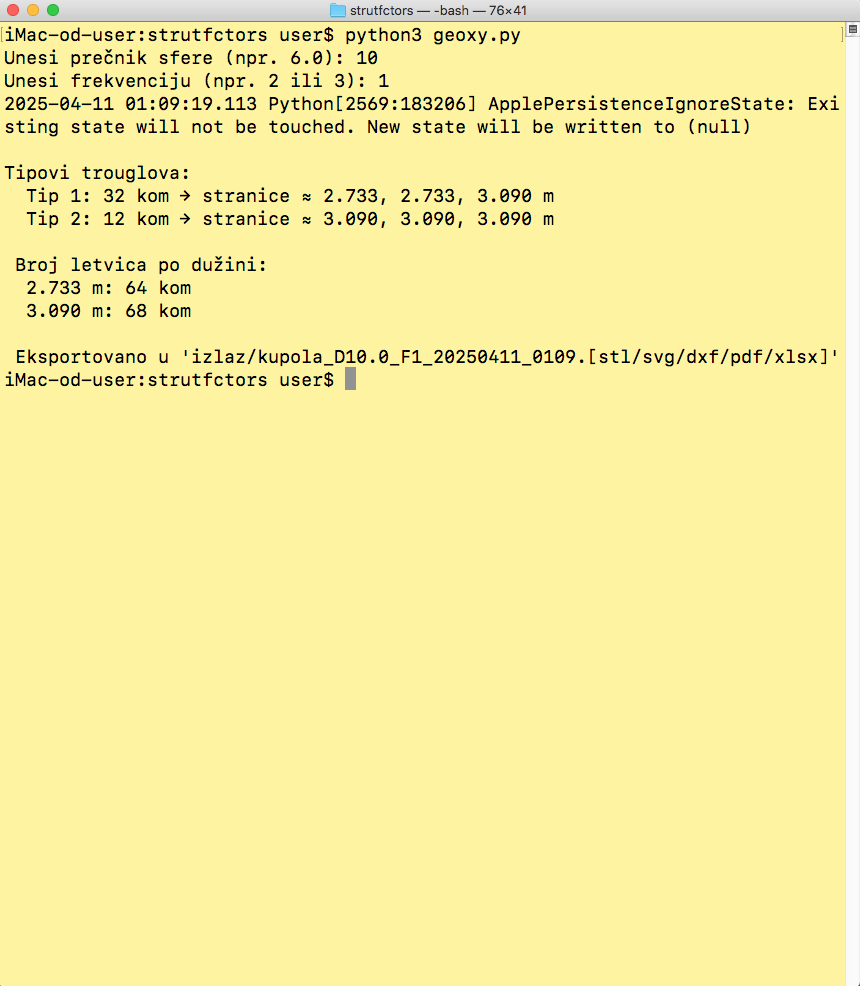
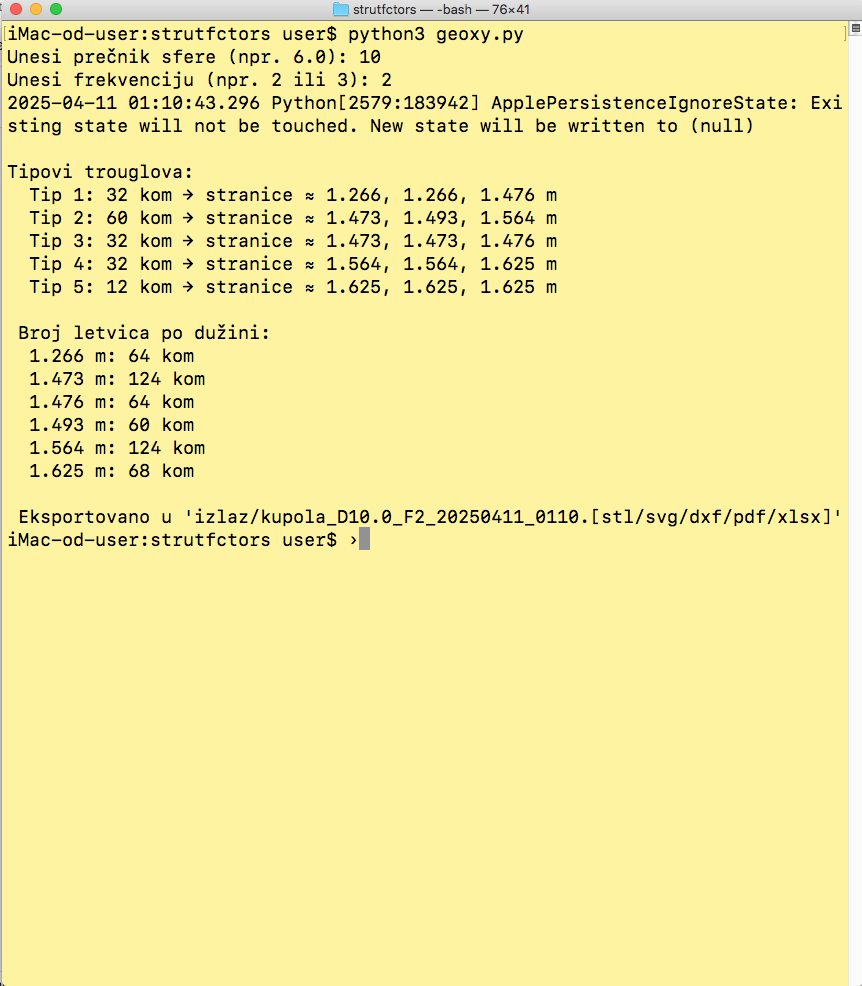
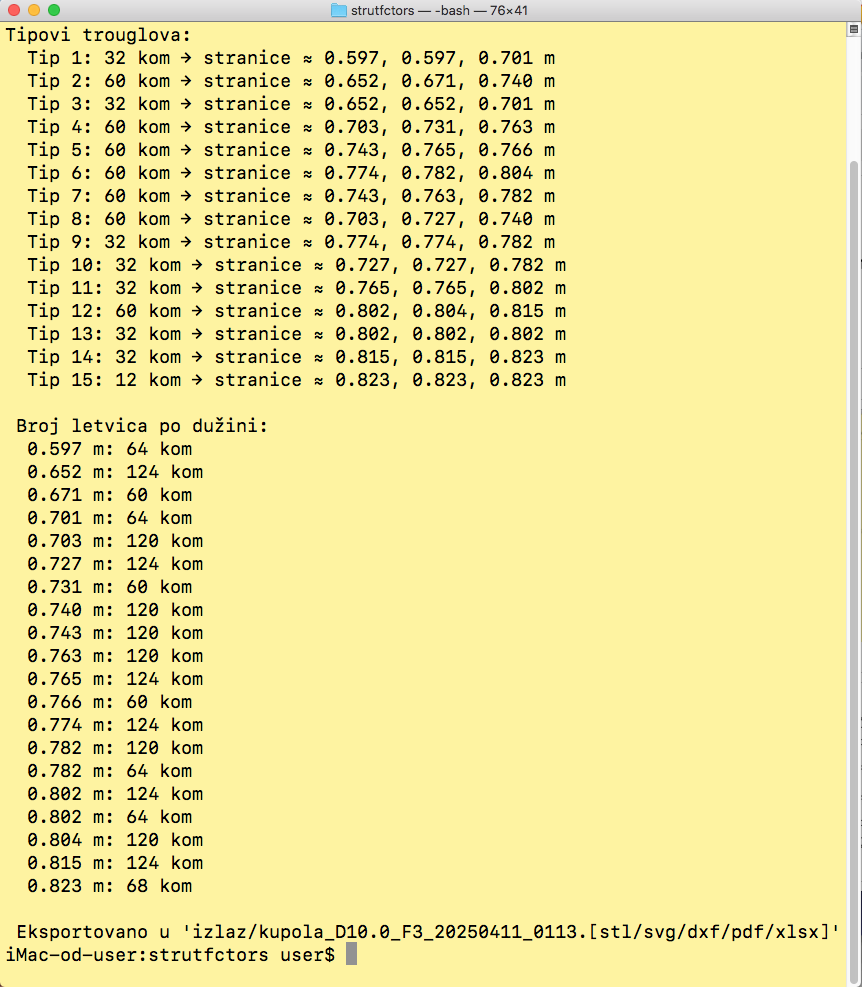
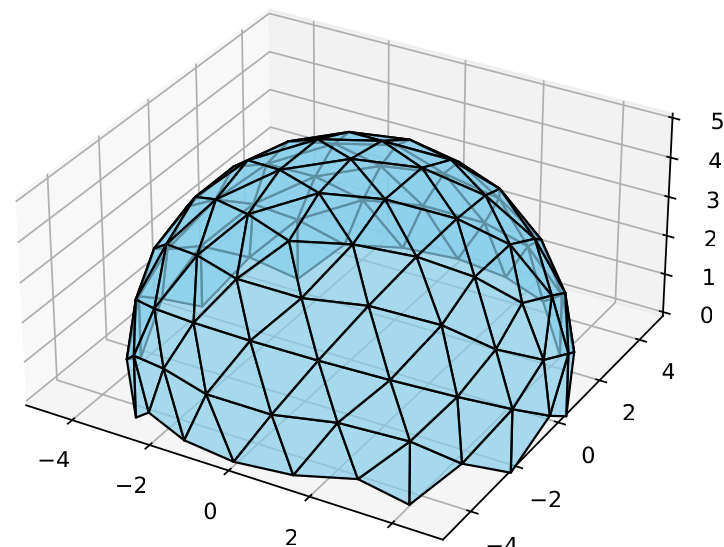
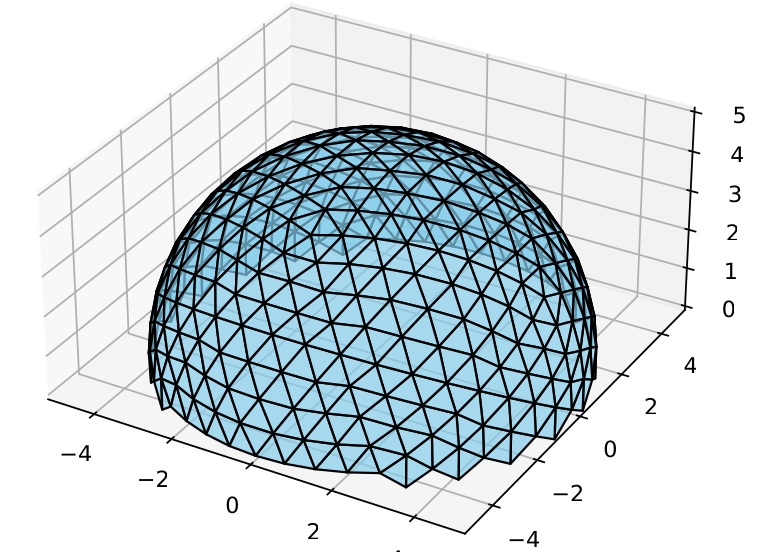
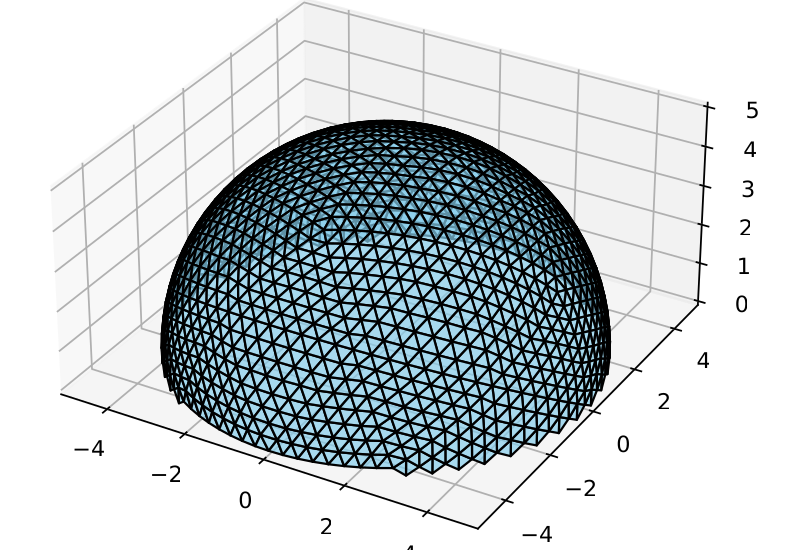
Rezultat rada programa geox.py:

Proračun za kupolu prečnika 10 m. Unos frekvencije je