Generator spiralne asimetrične helix zome kupole

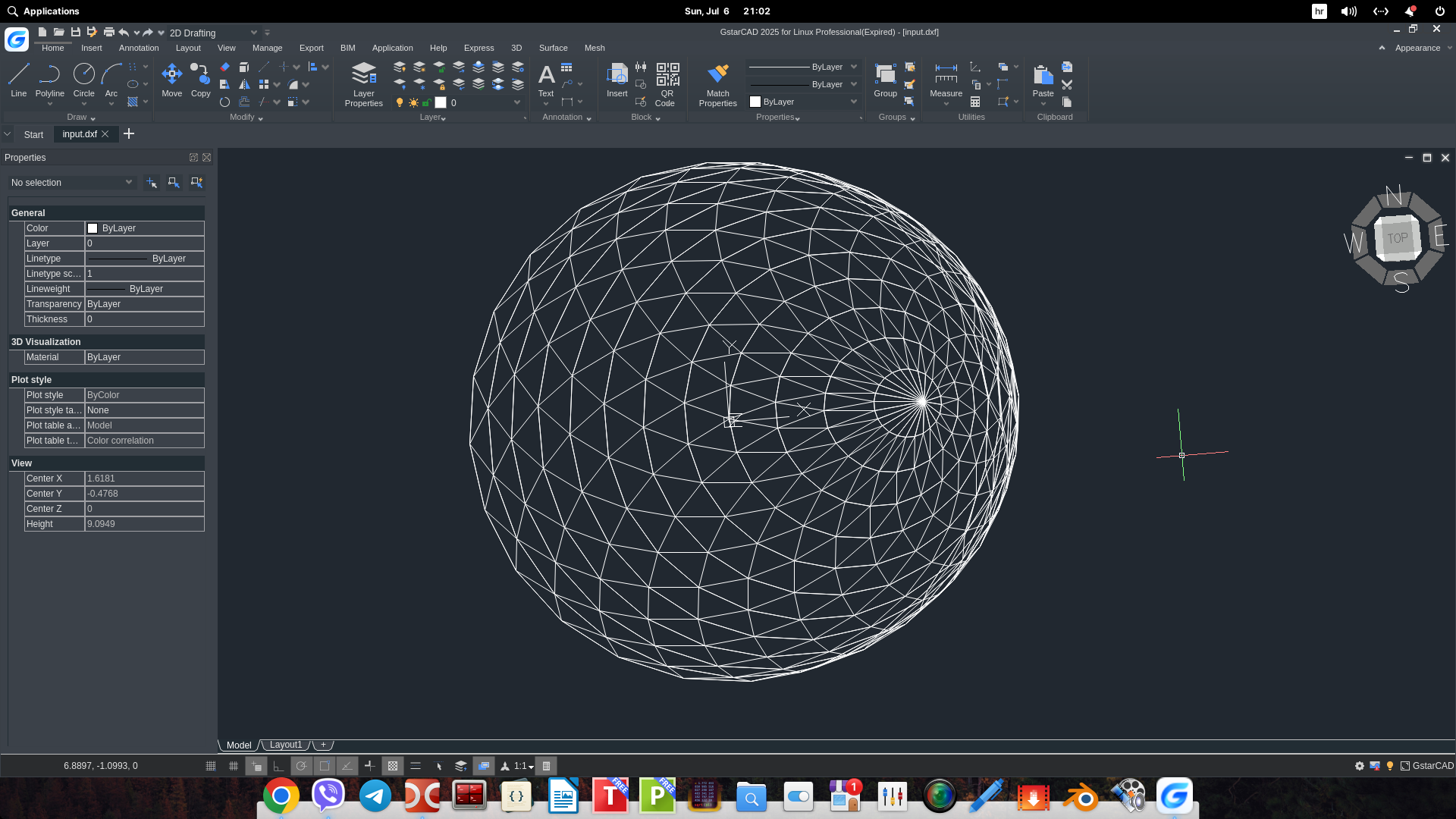
Predstavljeni Python program služi za generisanje 3D modela spiralne, asimetrične helix zome kupole i eksportovanje rezultata u OBJ format, prikladan za vizualizaciju i dalju obradu u 3D softverima.

Glavne komponente programa:

• Generisanje spirala (generate_spiral)
  Funkcija kreira set spiralnih linija u 3D prostoru koje čine osnovu kupole. Parametri omogućavaju definisanje broja spirala (n), broja segmenata po spirali (segs), prečnika baze kupole (d), visine (h), smera uvijanja spirale (direction), kao i asimetričnog pomaka centra (center_offset).
  Ova funkcija računa koordinate tačaka spiralnih linija koristeći trigonometrijske funkcije, gde se uvijanje i položaj prilagođavaju parametrima kako bi se dobio željeni oblik helix zome.
• Pronalazak preseka spirala (find_intersections)
  Dve grupe spirala – desne i leve – se međusobno presecaju u prostoru. Funkcija traži tačke koje su blizu jedne druge u 3D prostoru (uz zadatu toleranciju tol) i smatra ih presečnim tačkama.
  Ove presečne tačke služe za definisanje čvorova mreže kupole, što je bitno za formiranje čvrste, povezane strukture.
• Generisanje wireframe modela (generate_wireframe_from_intersections)
  Na osnovu pronađenih preseka, ova funkcija pravi OBJ fajl koji sadrži sve tačke (vrhove) i linije koje ih povezuju.
  Linije su povezane duž spirala i horizontalno između susednih spirala, stvarajući mrežu koja podseća na zome konstrukciju u vidu helix spirala.

Posebnosti programa:

• Kupola je asimetrična zahvaljujući pomaku centra (center_offset), što daje prirodniji, manje simetričan izgled.
• Koristi se kombinacija dve grupe spirala koje se uvijaju u suprotnim smerovima (direction=1 i direction=-1), što omogućava mrežastu strukturu sa čvrstim presekom.
• Eksport je u popularni OBJ format sa definisanim vrhovima i linijama, pogodan za 3D modeliranje, analize i štampu.

Praktična primena:

Ovakav generator može poslužiti arhitektama, inženjerima i entuzijastima 3D modelovanja za stvaranje inovativnih kupolastih konstrukcija, inspirisanih prirodnim i matematičkim formama. Posebno je koristan za istraživanje helix zome struktura sa asimetričnim pomacima i dinamičnim oblikovanjem.

Programski kod HelixA.py

Generator spiralne asimetrične helix zome kupole

Autor: Aleksandar Maričić
Licenca: MIT License

Pokretanje programa

U terminalu pokreni:

python3 helixAs.py

Unos parametara

Nakon pokretanja, program traži da uneseš sledeće vrednosti:

Ako pritisneš Enter bez unosa, koristi se ponuđena vrednost.

Rezultat

Program generiše .obj fajl koji sadrži žičani model preseka spirala sa horizontalnim linijama. Fajl možeš da otvoriš u bilo kom 3D programu (npr. Blender, MeshLab, FreeCAD).

Instalacija potrebnih zavisnosti:

python3 -m pip install numpy

Programski kod za helixAs.py

#helixAs.py
# The MIT License (MIT)
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovim se omogućava bilo kome da koristi, kopira, menja, spaja, objavljuje,
# distribuira, daje podlicencu i/ili prodaje kopije ovog softverskog programa,
# uz uslov da u svim kopijama ili značajnim delovima softverskog programa bude
# uključena sledeća obavest:
#
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovaj softverski program je pružen "takav kakav jeste", bez bilo kakvih garancija,
# izričitih ili impliciranih, uključujući, ali ne ograničavajući se na, garancije o
# prikladnosti za prodaju ili pogodnosti za određenu svrhu. U svakom slučaju, autori
# ili nosioci prava nisu odgovorni za bilo kakvu štetu ili druge obaveze koje mogu nastati
# usled upotrebe ovog softverskog programa.
# Naziv programa: Generator spiralne asimetrične helix zome kupole
# instalacija potrebnih zavisnosti: python3 -m pip install numpy


import numpy as np
from math import sin, cos, pi

def input_with_default(prompt, default, type_func=float):
    user_input = input(f"{prompt} [{default}]: ").strip()
    if user_input == '':
        return default
    try:
        return type_func(user_input)
    except ValueError:
        print(" Neispravan unos, koristi se podrazumevana vrednost.")
        return default

def generate_spiral(n, segs, d, h, direction, center_offset=np.array([0.0, 0.0])):
    spirals = []
    for i in range(n):
        beta = 2 * pi * i / n
        spiral = []
        for j in range(segs + 1):
            alpha = pi * j / segs
            theta = alpha if direction == 1 else -alpha

            offset_x = center_offset[0] * (alpha / pi)
            offset_y = center_offset[1] * (alpha / pi)

            x = sin(theta + beta) * d / 4 + sin(beta) * d / 4 + offset_x
            y = cos(theta + beta) * d / 4 + cos(beta) * d / 4 + offset_y
            z = (alpha / pi) * h
            spiral.append([x, y, z])
        spirals.append(np.array(spiral))
    return spirals

def find_intersections(spirals_right, spirals_left, tol=1e-2):
    intersections = []
    index_map = {}
    tol2 = tol * tol

    right_points = []
    right_map = []
    for si, spiral in enumerate(spirals_right):
        for pi, p in enumerate(spiral):
            right_points.append(p)
            right_map.append((si, pi))
    right_points = np.array(right_points)

    global_idx = 0
    for si_left, spiral_left in enumerate(spirals_left):
        for pi_left, p_left in enumerate(spiral_left):
            diffs = right_points - p_left
            dists2 = np.sum(diffs**2, axis=1)
            close_indices = np.where(dists2 < tol2)[0]
            if len(close_indices) > 0:
                key_left = ('L', si_left, pi_left)
                if key_left not in index_map:
                    index_map[key_left] = global_idx
                    intersections.append(p_left)
                    global_idx += 1
                for ci in close_indices:
                    si_right, pi_right = right_map[ci]
                    key_right = ('R', si_right, pi_right)
                    if key_right not in index_map:
                        index_map[key_right] = global_idx
                        intersections.append(right_points[ci])
                        global_idx += 1
    intersections = np.array(intersections)
    return intersections, index_map

def generate_wireframe_from_intersections(filename, spirals_right, spirals_left, index_map):
    lines = []

    def connect_intersections(side, spirals):
        for si, spiral in enumerate(spirals):
            intersect_indices = []
            for pi in range(len(spiral)):
                key = (side, si, pi)
                if key in index_map:
                    intersect_indices.append(index_map[key])
            for i in range(len(intersect_indices) - 1):
                lines.append((intersect_indices[i] + 1, intersect_indices[i + 1] + 1))

    connect_intersections('R', spirals_right)
    connect_intersections('L', spirals_left)

    def connect_horizontal_lines():
        for side, spirals in [('R', spirals_right), ('L', spirals_left)]:
            n = len(spirals)
            segs = len(spirals[0])
            for pi in range(segs):
                for si in range(n):
                    si_next = (si + 1) % n
                    key1 = (side, si, pi)
                    key2 = (side, si_next, pi)
                    if key1 in index_map and key2 in index_map:
                        lines.append((index_map[key1] + 1, index_map[key2] + 1))

    connect_horizontal_lines()

    with open(filename, 'w') as f:
        global_points = [None] * (max(index_map.values()) + 1)
        for key, idx in index_map.items():
            side, si, pi = key
            p = spirals_right[si][pi] if side == 'R' else spirals_left[si][pi]
            global_points[idx] = p
        for v in global_points:
            f.write(f"v {v[0]} {v[1]} {v[2]}\n")
        for line in lines:
            f.write(f"l {line[0]} {line[1]}\n")

    print(f"\n Izvezen wireframe model preseka sa horizontalnim linijama u '{filename}'")

# ---------------- MAIN ----------------
if __name__ == "__main__":
    print(" Unesi parametre za spiralnu asimetričnu helix zome kupolu (Enter za podrazumevane vrednosti)\n")

    filename = input("Naziv izlaznog fajla [.obj] [spiralna_asimetrična_helix_zome_kupola.obj]: ").strip()
    if filename == "":
        filename = "spiralna_asimetrična_helix_zome_kupola.obj"
    elif not filename.endswith(".obj"):
        filename += ".obj"

    n = input_with_default("Broj spirala (n)", 24, int)
    segs = input_with_default("Broj segmenata po spirali (segs)", 24, int)
    d = input_with_default("Prečnik spirale (d)", 8.0)
    h = input_with_default("Visina kupole (h)", 3.0)
    offset_x = input_with_default("Pomak centra u X pravcu", 3.0)
    offset_y = input_with_default("Pomak centra u Y pravcu", 0.0)
    tol = input_with_default("Tolerancija preseka", 0.02)

    center_offset = np.array([offset_x, offset_y])

    spirals_right = generate_spiral(n, segs, d, h, direction=1, center_offset=center_offset)
    spirals_left = generate_spiral(n, segs, d, h, direction=-1, center_offset=center_offset)

    intersections, index_map = find_intersections(spirals_right, spirals_left, tol=tol)
    generate_wireframe_from_intersections(filename, spirals_right, spirals_left, index_map)

Konverter OBJ modela u STL format sa triangulacijom

Ovaj Python program služi za konverziju 3D modela iz OBJ formata (koji sadrži vrhove i linije, odnosno žičani model) u STL format koji predstavlja model definisan trouglovima (površinama). Program automatski pronalazi trouglove u žičanom modelu i kreira pravilno orijentisane trouglaste površine pogodne za 3D štampu ili dalje 3D modelovanje.

Kako program funkcioniše:

1. Učitavanje OBJ fajla
   Program parsira OBJ fajl i čita sve vrhove (v x y z) i linije (l i j ...) koje povezuju te vrhove.
2. Eliminisanje duplikata vrhova
   Mnogi OBJ fajlovi imaju vrlo bliske ili duplirane koordinate vrhova. Program kombinuje vrhove koji su udaljeni manje od zadate tolerancije (podrazumevano 0.1) kako bi se smanjio broj vrhova.
3. Preslikavanje ivica na jedinstvene vrhove
   Nakon deduplikacije vrhova, linije se ažuriraju da koriste nove indekse vrhova.
4. Uklanjanje ukrštenih ivica
   Program detektuje ivice koje se preseku u prostoru i uklanja one koje su više usmerene vertikalno, zadržavajući horizontalnije veze. Ovo pomaže da se mreža očisti od neželjenih preseka.
5. Građenje grafa i pronalaženje trouglova
   Na osnovu preostalih ivica gradi se graf susednosti. Trouglovi se pronalaze traženjem trojki čvorova međusobno povezanih ivicama.
6. Orijentacija normala trouglova
   Kako bi se površine pravilno prikazale i model bio konzistentan, orijentacija normala trouglova se proverava i, ako treba, menja tako da gledaju “na spolja”.
7. Generisanje STL fajla
   Na kraju, svi trouglovi se upisuju u STL fajl, spreman za štampu ili druge primene.

Kako se koristi:

Pokretanje iz komandne linije:

python3 obj2stl_trianglovi.py ulazni_fajl.obj izlazni_fajl.stl

• ulazni_fajl.obj — putanja do ulaznog OBJ fajla sa vrhovima i linijama.
• izlazni_fajl.stl — putanja gde će biti sačuvan generisani STL fajl.

Zašto koristiti ovaj program?

• Pretvara žičane 3D modele u zatvorene trouglaste površine.
• Automatski pronalazi i pravi trouglove iz linija, čime štedi ručni rad.
• Uklanja problem ukrštanja linija koji može kvariti model.
• Orijentiše normale pravilno za 3D štampu.
• Koristan za brzo pretvaranje mreža u 3D štampljive objekte.

Instalacija potrebnih zavisnosti: python3 -m pip install numpy numpy-stl

python3 -m pip install numpy numpy-stl

Programski kod za obj2stl.py

#obj2stl.py
# The MIT License (MIT)
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovim se omogućava bilo kome da koristi, kopira, menja, spaja, objavljuje,
# distribuira, daje podlicencu i/ili prodaje kopije ovog softverskog programa,
# uz uslov da u svim kopijama ili značajnim delovima softverskog programa bude
# uključena sledeća obavest:
#
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovaj softverski program je pružen "takav kakav jeste", bez bilo kakvih garancija,
# izričitih ili impliciranih, uključujući, ali ne ograničavajući se na, garancije o
# prikladnosti za prodaju ili pogodnosti za određenu svrhu. U svakom slučaju, autori
# ili nosioci prava nisu odgovorni za bilo kakvu štetu ili druge obaveze koje mogu nastati
# usled upotrebe ovog softverskog programa.
# Naziv programa: Konverter OBJ modela u STL format sa triangulacijom
# Instalacija potrebnih zavisnosti: python3 -m pip install numpy numpy-stl


import sys
import numpy as np
from collections import defaultdict
from stl import mesh

def parse_obj(filename, tol=1e-3):
    vertices = []
    edges = []

    with open(filename, 'r') as f:
        for line in f:
            if line.startswith('v '):
                _, x, y, z = line.strip().split()
                vertices.append([float(x), float(y), float(z)])
            elif line.startswith('l '):
                parts = line.strip().split()
                indices = list(map(int, parts[1:]))
                for i in range(len(indices) - 1):
                    edges.append((indices[i] - 1, indices[i + 1] - 1))
    return np.array(vertices), edges

def deduplicate_vertices(vertices, tol=1e-1):
    unique = []
    index_map = {}
    for i, v in enumerate(vertices):
        for j, u in enumerate(unique):
            if np.linalg.norm(v - u) < tol:
                index_map[i] = j
                break
        else:
            index_map[i] = len(unique)
            unique.append(v)
    return np.array(unique), index_map

def remap_edges(edges, index_map):
    remapped = []
    for a, b in edges:
        a_m = index_map[a]
        b_m = index_map[b]
        if a_m != b_m:
            remapped.append((a_m, b_m))
    return remapped

def remove_crossing_edges_keep_horizontal(edges, vertices, tol=1e-5):
    def segments_intersect(p1, p2, q1, q2):
        u = p2 - p1
        v = q2 - q1
        w0 = p1 - q1
        a = np.dot(u, u)
        b = np.dot(u, v)
        c = np.dot(v, v)
        d = np.dot(u, w0)
        e = np.dot(v, w0)

        denom = a * c - b * b
        if abs(denom) < 1e-15:
            return False

        sc = (b * e - c * d) / denom
        tc = (a * e - b * d) / denom

        if not (0 <= sc <= 1 and 0 <= tc <= 1):
            return False

        pt1 = p1 + sc * u
        pt2 = q1 + tc * v
        return np.linalg.norm(pt1 - pt2) < tol

    def vertical_angle(p1, p2):
        v = p2 - p1
        norm = np.linalg.norm(v)
        if norm == 0:
            return np.pi / 2
        horizontal_proj = np.linalg.norm(v[:2])
        if horizontal_proj == 0:
            return np.pi / 2
        angle = np.arctan(abs(v[2]) / horizontal_proj)
        return angle

    edges_to_keep = set(range(len(edges)))
    for i in range(len(edges)):
        if i not in edges_to_keep:
            continue
        a1, a2 = edges[i]
        p1, p2 = vertices[a1], vertices[a2]
        for j in range(i + 1, len(edges)):
            if j not in edges_to_keep:
                continue
            b1, b2 = edges[j]
            if len({a1, a2, b1, b2}) < 4:
                continue
            q1, q2 = vertices[b1], vertices[b2]
            if segments_intersect(p1, p2, q1, q2):
                angle_i = vertical_angle(p1, p2)
                angle_j = vertical_angle(q1, q2)
                if angle_i <= angle_j:
                    edges_to_keep.discard(j)
                else:
                    edges_to_keep.discard(i)
                    break
    return [edges[i] for i in sorted(edges_to_keep)]

def build_graph(edges, num_vertices):
    graph = defaultdict(set)
    for a, b in edges:
        if a != b:
            graph[a].add(b)
            graph[b].add(a)
    return graph

def find_triangles(graph):
    triangles = set()
    for a in graph:
        neighbors_a = graph[a]
        for b in neighbors_a:
            if b <= a:
                continue
            neighbors_b = graph[b]
            common = neighbors_a.intersection(neighbors_b)
            for c in common:
                if c > b:
                    triangle = tuple(sorted([a, b, c]))
                    triangles.add(triangle)
    return list(triangles)

def compute_normal(v1, v2, v3):
    return np.cross(v2 - v1, v3 - v1)

def get_centroid(vertices):
    return np.mean(vertices, axis=0)

def ensure_outward_normals(triangles, vertices):
    centroid = get_centroid(vertices)
    corrected_triangles = []
    for tri in triangles:
        v1, v2, v3 = tri
        normal = compute_normal(v1, v2, v3)
        tri_center = np.mean([v1, v2, v3], axis=0)
        vec_from_centroid = tri_center - centroid
        if np.dot(normal, vec_from_centroid) < 0:
            tri = [v1, v3, v2]
        corrected_triangles.append(tri)
    return corrected_triangles

if __name__ == "__main__":
    if len(sys.argv) != 3:
        print("Upotreba: python3 obj2stl_trianglovi.py ulaz.obj izlaz.stl")
        sys.exit(1)

    obj_path = sys.argv[1]
    stl_path = sys.argv[2]

    print(f" Učitavanje OBJ: {obj_path}")
    verts_raw, edges = parse_obj(obj_path)
    print(f" Učitano {len(verts_raw)} vrhova i {len(edges)} linija.")

    verts, idx_map = deduplicate_vertices(verts_raw)
    print(f" Eliminisano na {len(verts)} jedinstvenih vrhova.")

    edges_mapped = remap_edges(edges, idx_map)
    print(f" Preslikani ivice na deduplicirane vrhove: {len(edges_mapped)} linija.")

    edges_clean = remove_crossing_edges_keep_horizontal(edges_mapped, verts)
    print(f" Uklonjeno {len(edges_mapped) - len(edges_clean)} ukrštenih linija.")

    graph = build_graph(edges_clean, len(verts))
    triangles_indices = find_triangles(graph)
    print(f" Pronađeno {len(triangles_indices)} trouglova.")

    # Pretvori indekse trouglova u vrhove
    triangles = []
    for tri_idx in triangles_indices:
        tri_vertices = [verts[i] for i in tri_idx]
        triangles.append(tri_vertices)

    # Osiguraj da su trouglovi orijentisani spolja
    triangles = ensure_outward_normals(triangles, verts)

    # Kreiraj STL
    stl_data = mesh.Mesh(np.zeros(len(triangles), dtype=mesh.Mesh.dtype))
    for i, tri in enumerate(triangles):
        stl_data.vectors[i] = np.array(tri)

    stl_data.save(stl_path)
    print(f" Sačuvan STL: {stl_path} ({len(triangles)} trouglova)")

Konvertor OBJ žičanih modela u obojeni PLY format sa cilindričnim šipkama

Ovaj Python program omogućava konverziju 3D žičanih modela iz OBJ formata (sa definisanim vrhovima i linijama) u PLY format koji koristi cilindrične štapove (cevi) za prikaz ivica, sa izabranom bojom. Program generiše geometriju šipki između vrhova i čuva model u standardnom PLY fajlu sa RGB bojom.

Kako program radi:

• Učita OBJ fajl i izvlači vrhove i linije (ivice).
• Koristi definisanu debljinu i broj segmenata da na svakoj liniji napravi trodimenzionalni cilindar kao 3D geometrijski objekat.
• Omogućava korisniku da izabere boju šipki iz ponuđenog menija.
• Kreira PLY fajl koji sadrži vertexe i trouglaste površine cilindara, sa dodatim RGB vrednostima boje za svaki vertex.
• Čuva rezultat u istom direktorijumu, sa istim imenom kao ulazni fajl, ali sa ekstenzijom .ply.

Kako koristiti program:

1. Pokrenite program iz komandne linije sa ulaznim OBJ fajlom:

python3 obj2ply.py model.obj

2. Program će prikazati meni sa bojama. Unesite broj boje koju želite za model (npr. 4 za plavu).
3. Nakon obrade, u istom folderu će biti kreiran model.ply fajl sa cilindričnim šipkama u izabranoj boji.

Ključne karakteristike:

• Cilindrična reprezentacija ivica: Svaka linija u OBJ fajlu pretvara se u 3D cilindar, što omogućava lepši i realističniji prikaz šipkastih konstrukcija.
• Više ponuđenih boja: Korisnik može lako da bira boju šipki putem jednostavnog menija.
• Jednostavna upotreba: Program se koristi samo sa jednim argumentom – ulaznim OBJ fajlom.
• Otvoreni kod sa MIT licencom: Može se slobodno koristiti i prilagođavati uz navođenje autora.

Instalacija potrebnih zavisnosti:

 python3 -m pip install numpy

Programski kod zao bj2stl.py

#obj2stl.py
# The MIT License (MIT)
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovim se omogućava bilo kome da koristi, kopira, menja, spaja, objavljuje,
# distribuira, daje podlicencu i/ili prodaje kopije ovog softverskog programa,
# uz uslov da u svim kopijama ili značajnim delovima softverskog programa bude
# uključena sledeća obavest:
#
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovaj softverski program je pružen "takav kakav jeste", bez bilo kakvih garancija,
# izričitih ili impliciranih, uključujući, ali ne ograničavajući se na, garancije o
# prikladnosti za prodaju ili pogodnosti za određenu svrhu. U svakom slučaju, autori
# ili nosioci prava nisu odgovorni za bilo kakvu štetu ili druge obaveze koje mogu nastati
# usled upotrebe ovog softverskog programa.
# Naziv programa: KONVERTOR IZ OBJ U PLY
# Instalacija potrebnih zavisnosti: python3 -m pip install numpy



import numpy as np
import sys
from pathlib import Path

RADIUS = 0.01
CYLINDER_SEGMENTS = 16

# Definiši dostupne boje kao RGB (0-255)
BOJE = {
    1: ("bela", (255, 255, 255)),
    2: ("crvena", (255, 0, 0)),
    3: ("zelena", (0, 255, 0)),
    4: ("plava", (0, 0, 255)),
    5: ("žuta", (255, 255, 0)),
    6: ("ljubičasta", (128, 0, 128)),
    7: ("narandžasta", (255, 165, 0)),
    8: ("tirkizna", (64, 224, 208)),
    9: ("siva", (128, 128, 128)),
    10: ("crna", (0, 0, 0)),
}


def prikazi_meni_i_uzmi_boju():
    print("Izaberite boju modela:")
    for broj, (ime, rgb) in sorted(BOJE.items()):
        print(f"{broj}. {ime} (RGB: {rgb})")
    while True:
        try:
            izbor = int(input("Unesite broj boje: "))
            if izbor in BOJE:
                return BOJE[izbor][1]
            else:
                print("Nepoznat broj boje, pokušajte ponovo.")
        except ValueError:
            print("Molimo unesite ceo broj.")


def ucitaj_obj(path):
    vertices = []
    edges = []
    with open(path, "r") as f:
        for line in f:
            if line.startswith("v "):
                _, x, y, z = line.strip().split()
                vertices.append(np.array([float(x), float(y), float(z)]))
            elif line.startswith("l "):
                parts = line.strip().split()
                edges.append((int(parts[1]) - 1, int(parts[2]) - 1))
    return vertices, edges


def napravi_cilindar(p1, p2, radius, segments=16):
    v = p2 - p1
    length = np.linalg.norm(v)
    if length < 1e-8:
        return [], []

    axis = v / length

    if abs(axis[0]) < 0.001 and abs(axis[1]) < 0.001:
        ortho = np.array([1, 0, 0])
    else:
        ortho = np.array([0, 0, 1])

    n1 = np.cross(axis, ortho)
    n1 /= np.linalg.norm(n1)
    n2 = np.cross(axis, n1)
    n2 /= np.linalg.norm(n2)

    circle_p1 = []
    circle_p2 = []
    for i in range(segments):
        theta = 2 * np.pi * i / segments
        dir_vec = np.cos(theta) * n1 + np.sin(theta) * n2
        circle_p1.append(p1 + radius * dir_vec)
        circle_p2.append(p2 + radius * dir_vec)

    vertices = circle_p1 + circle_p2
    faces = []

    for i in range(segments):
        i_next = (i + 1) % segments
        faces.append((i, i_next, i_next + segments))
        faces.append((i, i_next + segments, i + segments))

    return vertices, faces


def sacuvaj_ply(verts, faces, filename, boja):
    r, g, b = boja
    with open(filename, "w") as f:
        f.write("ply\n")
        f.write("format ascii 1.0\n")
        f.write(f"element vertex {len(verts)}\n")
        f.write("property float x\nproperty float y\nproperty float z\n")
        # Dodajemo RGB atribute
        f.write("property uchar red\nproperty uchar green\nproperty uchar blue\n")
        f.write(f"element face {len(faces)}\n")
        f.write("property list uchar int vertex_indices\n")
        f.write("end_header\n")

        for v in verts:
            f.write(f"{v[0]} {v[1]} {v[2]} {r} {g} {b}\n")

        for face in faces:
            f.write(f"3 {face[0]} {face[1]} {face[2]}\n")


def main():
    if len(sys.argv) != 2:
        print("Upotreba: python3 obj2ply.py ulazni_fajl.obj")
        return

    input_path = Path(sys.argv[1])
    if not input_path.exists():
        print(f"Fajl ne postoji: {input_path}")
        return

    boja = prikazi_meni_i_uzmi_boju()

    output_path = input_path.with_suffix(".ply")

    vertices, edges = ucitaj_obj(input_path)
    print(f"Učitano {len(vertices)} tačaka i {len(edges)} ivica iz {input_path}")

    sve_verteksi = []
    sve_face = []
    offset = 0

    for i1, i2 in edges:
        p1 = vertices[i1]
        p2 = vertices[i2]

        verts_cil, faces_cil = napravi_cilindar(p1, p2, RADIUS, CYLINDER_SEGMENTS)

        sve_verteksi.extend(verts_cil)
        for f in faces_cil:
            sve_face.append((f[0] + offset, f[1] + offset, f[2] + offset))

        offset += len(verts_cil)

    sacuvaj_ply(sve_verteksi, sve_face, output_path, boja)
    print(f"Ply fajl sa šipkama sačuvan kao: {output_path}")


if __name__ == "__main__":
    main()

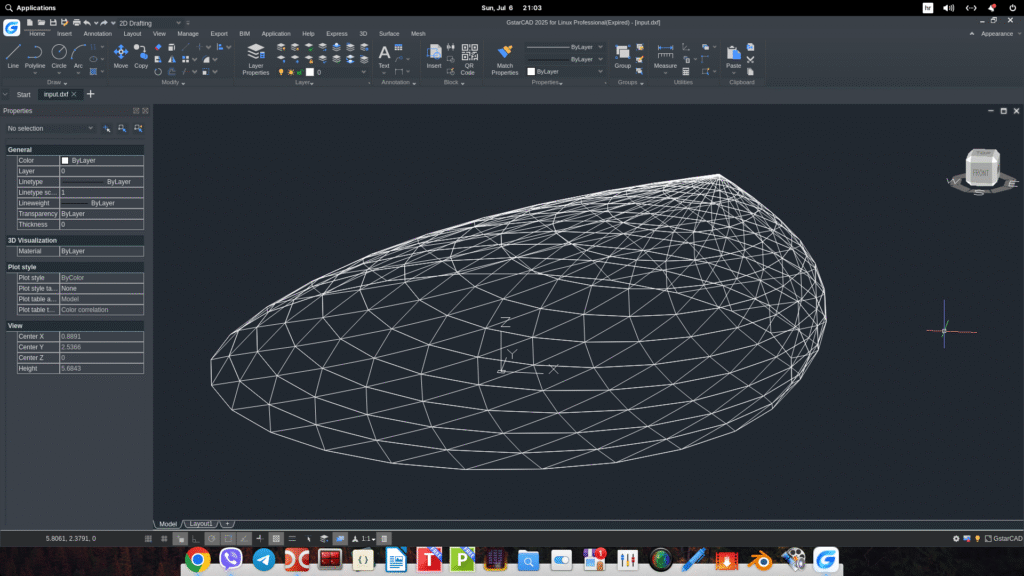
Konvertor OBJ modela u DXF format

Ovaj Python program omogućava konverziju 3D žičanih modela iz OBJ formata u DXF format. Program učitava vrhove i linije iz OBJ fajla i u DXF fajlu ih prenosi kao linijske entitete, što olakšava rad u CAD programima poput AutoCAD-a.

Kako program funkcioniše:

• Učitava OBJ fajl i parsira vrhove (v x y z) i linije (l i j) koje povezuju te vrhove.
• Kreira novi DXF dokument koristeći biblioteku ezdxf.
• Dodaje linije između odgovarajućih tačaka u model prostor DXF fajla.
• Čuva rezultat kao DXF fajl sa istim imenom kao ulazni, ali sa .dxf ekstenzijom.

Kako koristiti program:

1. Pokrenite program iz komandne linije sa ulaznim OBJ fajlom:

python3 obj2dxf.py model.obj

2. Program će automatski kreirati model.dxf u istom direktorijumu.

Prednosti:

• Jednostavan i brz način da se OBJ žičani modeli prenesu u CAD okruženje.
• Koristi standardni DXF format verzije R2010.
• Ne zahteva dodatnu konfiguraciju osim zadavanja ulaznog fajla.

Instalacija potrebnih zavisnosti:

python3 -m pip install ezdxf

Programski kod za obj2dxf.py

#obj2dxf.py
# The MIT License (MIT)
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovim se omogućava bilo kome da koristi, kopira, menja, spaja, objavljuje,
# distribuira, daje podlicencu i/ili prodaje kopije ovog softverskog programa,
# uz uslov da u svim kopijama ili značajnim delovima softverskog programa bude
# uključena sledeća obavest:
#
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovaj softverski program je pružen "takav kakav jeste", bez bilo kakvih garancija,
# izričitih ili impliciranih, uključujući, ali ne ograničavajući se na, garancije o
# prikladnosti za prodaju ili pogodnosti za određenu svrhu. U svakom slučaju, autori
# ili nosioci prava nisu odgovorni za bilo kakvu štetu ili druge obaveze koje mogu nastati
# usled upotrebe ovog softverskog programa.
# Naziv programa: KONVERTOR IZ OBJ U DXF
# Instalacija potrebnih zavisnosti: python3 -m pip install ezdxf


import ezdxf
import sys
from pathlib import Path


def read_obj_vertices_and_lines(filename):
    vertices = []
    lines = []

    with open(filename, 'r') as f:
        for line in f:
            if line.startswith('v '):
                parts = line.strip().split()
                x, y, z = float(parts[1]), float(parts[2]), float(parts[3])
                vertices.append((x, y, z))
            elif line.startswith('l '):
                parts = line.strip().split()
                i1 = int(parts[1]) - 1
                i2 = int(parts[2]) - 1
                lines.append((i1, i2))

    return vertices, lines


def obj_to_dxf(obj_file, dxf_file):
    vertices, lines = read_obj_vertices_and_lines(obj_file)
    doc = ezdxf.new(dxfversion="R2010")
    msp = doc.modelspace()

    for i1, i2 in lines:
        p1 = vertices[i1]
        p2 = vertices[i2]
        msp.add_line(p1, p2)

    doc.saveas(dxf_file)
    print(f" Sačuvan: {dxf_file}")


def main():
    if len(sys.argv) != 2:
        print("Upotreba: python3 obj2dxf.py ulazni_fajl.obj")
        return

    input_path = Path(sys.argv[1])
    if not input_path.exists():
        print(f" Fajl ne postoji: {input_path}")
        return

    output_path = input_path.with_suffix('.dxf')
    obj_to_dxf(str(input_path), str(output_path))


if __name__ == "__main__":
    main()

Statistika i montažna shema kupole statL.py

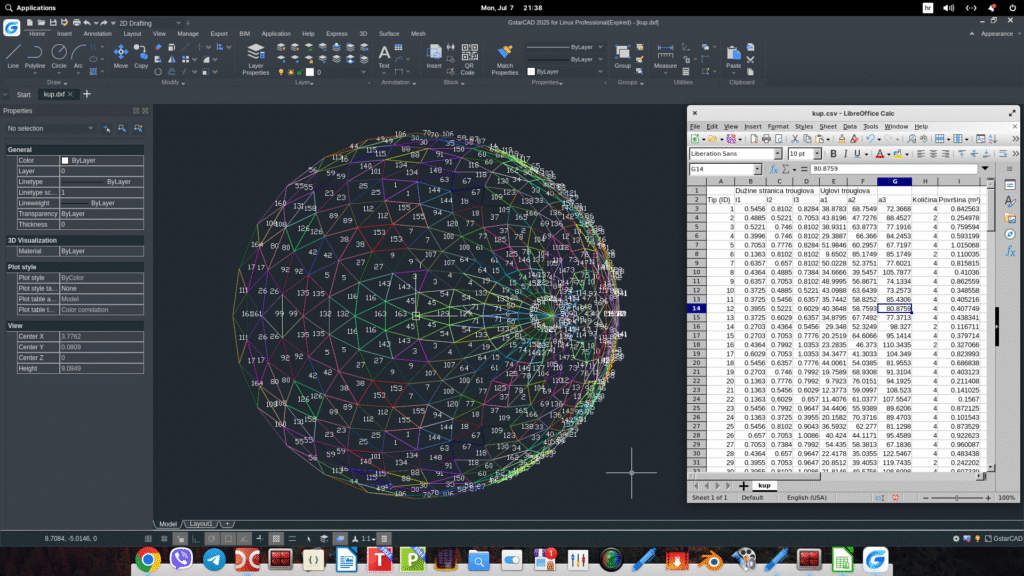
Opis programa statL.py

Ovaj Python program služi za analizu trouglastih mreža učitanih iz STL fajla. On grupiše trouglove prema njihovim geometrijskim karakteristikama — tačnije po dužinama stranica i uglovima trouglova — i zatim generiše detaljan izveštaj i vizualizacije na osnovu tih grupa.

Šta program radi?

1. Učitava STL fajl koji sadrži model definisan trouglastom mrežom.
2. Izračunava geometrijske karakteristike svakog trougla:
   • Dužine stranica,
   • Uglove između stranica,
   • Površinu trougla.
3. Grupše trouglove u tipove — trouglovi sa vrlo sličnim dimenzijama i uglovima dobijaju isti tip (ID).
4. Pravi statistiku po tipovima:
   • Broj trouglova svakog tipa,
   • Ukupna površina trouglova tog tipa.
5. Generiše tri izlazna fajla sa različitim informacijama i formatima:
   • CSV fajl (<ime> .csv)
     Sadrži tabelarni izveštaj sa informacijama o svakom tipu trougla: njihove dimenzije, uglove, broj pojavljivanja i ukupnu površinu.
     Koristi se za analizu i pregled podataka u tabelarnom obliku, npr. u Excel-u.
   • STL fajl sa oznakama (<ime>_labeled.stl)
     STL fajl koji sadrži iste trouglove, ali svaki trougao ima dodeljen atribut (labelu) koji označava njegov tip.
     Može se koristiti za dalje CAD analize ili vizualizacije u programima koji podržavaju atribute u STL-u.
   • PLY fajl sa bojama (<ime>.ply)
     Trojdimenzionalni fajl sa bojama, gde su trouglovi obojeni različitim bojama prema tipu.
     Može se pregledati u softverima za 3D vizualizaciju koji podržavaju PLY format i boje.
   • DXF fajl (<ime>.dxf)
     CAD fajl koji sadrži trouglove i numeričke oznake tipova direktno nacrtane u 3D prostoru.
     Namenjen je za pregled i dalje CAD obrade u programima poput AutoCAD-a, BricsCAD-a ili drugih CAD alata.
     Obeležavanje trouglova pomaže u brzom prepoznavanju i razlikovanju tipova na nacrtu.

Zašto koristiti ovaj program?

• Kada imate STL model sa mnogo trouglova i želite da razumete njegovu geometrijsku strukturu.
• Ako želite da klasifikujete trouglove prema njihovim obliku i dimenzijama radi kvalitativne analize.
• Da dobijete tabelarni pregled statistike za različite tipove trouglova.
• Da vizualizujete grupisane trouglove u boji (PLY fajl).
• Da napravite CAD dokument sa označenim i obeleženim tipovima trouglova za dalju tehničku obradu.

Kako se koristi?

U komandnoj liniji pokrenite:

python3 statL.py model.stl

Gde je model.stl ulazni STL fajl sa trouglastom mrežom.

Nakon izvršenja, u istom direktorijumu dobićete:

• model.csv — CSV izveštaj sa detaljima o tipovima trouglova.
• model_labeled.stl — STL fajl sa oznakama tipova trouglova.
• model.ply — PLY fajl sa bojama po tipovima.
• model.dxf — DXF fajl sa 3D trouglovima i brojčanim oznakama tipova.

Instalacija potrebnih zavisnosti:

python3 -m pip install numpy numpy-stl plyfile

Programski kod za statL.py

#statL.py
# The MIT License (MIT)
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovim se omogućava bilo kome da koristi, kopira, menja, spaja, objavljuje,
# distribuira, daje podlicencu i/ili prodaje kopije ovog softverskog programa,
# uz uslov da u svim kopijama ili značajnim delovima softverskog programa bude
# uključena sledeća obavest:
#
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovaj softverski program je pružen "takav kakav jeste", bez bilo kakvih garancija,
# izričitih ili impliciranih, uključujući, ali ne ograničavajući se na, garancije o
# prikladnosti za prodaju ili pogodnosti za određenu svrhu. U svakom slučaju, autori
# ili nosioci prava nisu odgovorni za bilo kakvu štetu ili druge obaveze koje mogu nastati
# usled upotrebe ovog softverskog programa.
# Naziv programa: Statistika i montažna shema kupole statL.py
# Instalacija potrebnih zavisnosti:python3 -m pip install numpy numpy-stl plyfile





import sys
import numpy as np
from stl import mesh
from collections import defaultdict
from math import acos, degrees
from plyfile import PlyData, PlyElement

def side_lengths(triangle):
    a = np.linalg.norm(triangle[1] - triangle[0])
    b = np.linalg.norm(triangle[2] - triangle[1])
    c = np.linalg.norm(triangle[0] - triangle[2])
    return sorted([a, b, c])

def angles(triangle):
    a, b, c = triangle
    ab = b - a
    bc = c - b
    ca = a - c
    def angle(u, v):
        cos_theta = np.dot(u, v) / (np.linalg.norm(u) * np.linalg.norm(v))
        return degrees(acos(np.clip(cos_theta, -1.0, 1.0)))
    return sorted([
        angle(ab, -ca),
        angle(bc, -ab),
        angle(ca, -bc)
    ])

def triangle_area(triangle):
    a = np.linalg.norm(triangle[1] - triangle[0])
    b = np.linalg.norm(triangle[2] - triangle[1])
    c = np.linalg.norm(triangle[0] - triangle[2])
    s = (a + b + c) / 2
    area = max(s * (s - a) * (s - b) * (s - c), 0)
    return np.sqrt(area)

def normalize_tuple(lst, tol=1e-4):
    return tuple(round(x, 4) for x in lst)

def group_triangles(triangles):
    groups = {}
    labels = []
    group_stats = defaultdict(lambda: {"count": 0, "area": 0.0})
    index = 1
    for tri in triangles:
        sides = side_lengths(tri)
        angs = angles(tri)
        key = (normalize_tuple(sides), normalize_tuple(angs))
        if key not in groups:
            groups[key] = index
            index += 1
        label = groups[key]
        labels.append(label)
        group_stats[label]["count"] += 1
        group_stats[label]["area"] += triangle_area(tri)
    return labels, group_stats, groups

def save_csv(report_path, group_stats, groups):
    with open(report_path, 'w') as f:
        f.write(",Dužine stranica trouglova,,,Uglovi trouglova,,,," + "\n")
        f.write("Tip (ID),l1,l2,l3,a1,a2,a3,Broj trouglova,Ukupna površina (m²)\n")
        sorted_items = sorted(groups.items(), key=lambda x: groups[x[0]])
        for key, label in sorted_items:
            sides, angles = key
            count = group_stats[label]["count"]
            area = group_stats[label]["area"]
            row = f"{label}," + ",".join(map(str, sides)) + "," + ",".join(map(str, angles)) + f",{count},{round(area, 6)}"
            f.write(row + "\n")

def generate_colors(n):
    np.random.seed(0)
    return [tuple(np.random.randint(0, 255, 3)) for _ in range(n + 1)]

def export_colored_ply(triangles, triangle_labels, output_path):
    vertex_list = []
    face_list = []
    vertex_map = {}
    idx = 0
    for i, tri in enumerate(triangles):
        face_indices = []
        for v in tri:
            key = tuple(np.round(v, 8))
            if key not in vertex_map:
                vertex_map[key] = idx
                vertex_list.append((*key,))
                idx += 1
            face_indices.append(vertex_map[key])
        face_list.append((face_indices, triangle_labels[i]))

    types = set(triangle_labels)
    colors = generate_colors(len(types))
    type_to_color = {typ: colors[i] for i, typ in enumerate(sorted(types))}

    vertex_dtype = [('x', 'f4'), ('y', 'f4'), ('z', 'f4')]
    vertices_np = np.array(vertex_list, dtype=vertex_dtype)

    face_dtype = [('vertex_indices', 'i4', (3,)), ('red', 'u1'), ('green', 'u1'), ('blue', 'u1')]
    faces_np = np.empty(len(face_list), dtype=face_dtype)
    for i, (indices, label) in enumerate(face_list):
        faces_np[i]['vertex_indices'] = indices
        r, g, b = type_to_color[label]
        faces_np[i]['red'] = r
        faces_np[i]['green'] = g
        faces_np[i]['blue'] = b

    el_verts = PlyElement.describe(vertices_np, 'vertex')
    el_faces = PlyElement.describe(faces_np, 'face')
    PlyData([el_verts, el_faces], text=True).write(output_path)

def export_dxf(triangles, triangle_labels, output_path):
    import ezdxf
    from ezdxf.entities import Face3d
    from ezdxf.lldxf.const import DXFValueError

    doc = ezdxf.new(dxfversion="R2010")
    msp = doc.modelspace()

    colors = generate_colors(max(triangle_labels))
    type_to_color = {typ: colors[typ] for typ in set(triangle_labels)}

    for typ in set(triangle_labels):
        layer_name = f"TIP_{typ}"
        if layer_name not in doc.layers:
            doc.layers.add(name=layer_name)

    for tri, label in zip(triangles, triangle_labels):
        layer = f"TIP_{label}"
        r, g, b = type_to_color[label]

        points = [tuple(tri[0]), tuple(tri[1]), tuple(tri[2]), tuple(tri[2])]
        try:
            face = Face3d.new(dxfattribs={
                'layer': layer,
                'true_color': (r << 16) + (g << 8) + b
            })
            face.dxf.vtx0 = points[0]
            face.dxf.vtx1 = points[1]
            face.dxf.vtx2 = points[2]
            face.dxf.vtx3 = points[3]
            msp.add_entity(face)
        except DXFValueError:
            continue

        center = tuple(np.mean(tri, axis=0))
        text = msp.add_text(
            str(label),
            dxfattribs={
                'height': 0.1,
                'layer': layer
            }
        )
        text.dxf.insert = center

    doc.saveas(output_path)

def main():
    if len(sys.argv) != 2:
        print("Upotreba: python3 statL.py model.stl")
        return

    stl_file = sys.argv[1]
    base = stl_file.rsplit('.', 1)[0]
    csv_path = base + '.csv'
    stl_labeled = base + '_labeled.stl'
    ply_path = base + '.ply'
    dxf_path = base + '.dxf'

    stl_mesh = mesh.Mesh.from_file(stl_file)
    triangles = stl_mesh.vectors

    triangle_labels, stats, key_map = group_triangles(triangles)

    save_csv(csv_path, stats, key_map)
    print(f"📄 CSV izveštaj sačuvan kao: {csv_path}")

    labeled_mesh = mesh.Mesh(np.zeros(len(triangles), dtype=mesh.Mesh.dtype))
    for i in range(len(triangles)):
        labeled_mesh.vectors[i] = triangles[i]
        labeled_mesh.attr[i] = triangle_labels[i]
    labeled_mesh.save(stl_labeled)
    print(f" STL sa oznakama sačuvan kao: {stl_labeled}")

    export_colored_ply(triangles, triangle_labels, ply_path)
    print(f" PLY sa bojama sačuvan kao: {ply_path}")

    export_dxf(triangles, triangle_labels, dxf_path)
    print(f" DXF sa tipovima sačuvan kao: {dxf_path}")

if __name__ == "__main__":
    main()

Linkovi: