Generator spiralne kupole

Program helix.py služi za generisanje žičanog modela spiralne kupole na osnovu ukrštanja dve grupe spirala – levih i desnih – koje se prostiru duž površine polukupole. Ove spirale se modeluju matematički, a njihova ukrštanja formiraju mrežu tačaka (čvorišta) koja može da se koristi za dalje modeliranje, analizu ili vizualizaciju geometrijskih struktura.

Funkcionalnosti:

• Korisnik unosi:
  • broj spirala po smeru (leva i desna),
  • broj segmenata po spirali,
  • prečnik baze kupole,
  • visinu kupole,
  • naziv izlaznog .obj fajla (fajl sa 3D tačkama i linijama).
• Program automatski generiše spirale u prostoru.
• Izračunava se gde se spirale međusobno seku (preseci se određuju uz malu toleranciju).
• Formira se mreža povezivanjem tih presečnih tačaka.
• Na kraju, rezultat se čuva u standardnom OBJ fajl formatu (kompatibilan sa mnogim 3D softverima poput Blender-a).

Upotreba:

Pokrenite program u komandnoj liniji:

python helix.py

Zatim pratite uputstva za unos parametara. Ako pritisnete Enter bez unosa, koristiće se podrazumevane vrednosti.

Programski kod helix.py:

# The MIT License (MIT)
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovim se omogućava bilo kome da koristi, kopira, menja, spaja, objavljuje,
# distribuira, daje podlicencu i/ili prodaje kopije ovog softverskog programa,
# uz uslov da u svim kopijama ili značajnim delovima softverskog programa bude
# uključena sledeća obavest:
#
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovaj softverski program je pružen "takav kakav jeste", bez bilo kakvih garancija,
# izričitih ili impliciranih, uključujući, ali ne ograničavajući se na, garancije o
# prikladnosti za prodaju ili pogodnosti za određenu svrhu. U svakom slučaju, autori
# ili nosioci prava nisu odgovorni za bilo kakvu štetu ili druge obaveze koje mogu nastati
# usled upotrebe ovog softverskog programa.
# Naziv programa: GENERATOR SPIRALNE KUPOLE


import numpy as np
from math import sin, cos, pi
from scipy.spatial import cKDTree
from collections import defaultdict, deque

def generate_spiral(n, segs, d, h, direction):
    spirals = []
    for i in range(n):
        beta = 2 * pi * i / n
        spiral = []
        for j in range(segs + 1):
            alpha = pi * j / segs
            theta = alpha if direction == 1 else -alpha
            x = sin(theta + beta) * d/4 + sin(beta)*d/4
            y = cos(theta + beta) * d/4 + cos(beta)*d/4
            z = (alpha/pi) * h
            spiral.append([x, y, z])
        spirals.append(np.array(spiral))
    return spirals

def find_intersections(spirals1, spirals2, tol=1e-4):
    points1 = np.vstack(spirals1)
    tree = cKDTree(points1)

    intersections = []
    for spiral in spirals2:
        for p in spiral:
            dist, idx = tree.query(p, distance_upper_bound=tol)
            if dist < tol:
                match = points1[idx]
                intersections.append(tuple(np.round(match, 5)))
    return list(dict.fromkeys(intersections))

def build_graph(intersections, spirals, tol=1e-4):
    point_idx = {p: i + 1 for i, p in enumerate(intersections)}
    edges = set()

    for spiral in spirals:
        prev = None
        for p in spiral:
            p_rounded = tuple(np.round(p, 5))
            if p_rounded in point_idx:
                if prev is not None:
                    edges.add((min(prev, point_idx[p_rounded]), max(prev, point_idx[p_rounded])))
                prev = point_idx[p_rounded]
    return point_idx, edges

def sort_face_vertices(face_indices, vertex_lookup):
    points = np.array([vertex_lookup[i] for i in face_indices])
    center = np.mean(points, axis=0)
    v1 = points[0] - center
    normal = np.cross(points[1] - points[0], points[2] - points[0])
    normal /= np.linalg.norm(normal)
    axis_x = v1 / np.linalg.norm(v1)
    axis_y = np.cross(normal, axis_x)
    angles = []
    for p in points:
        vec = p - center
        x = np.dot(vec, axis_x)
        y = np.dot(vec, axis_y)
        angle = np.arctan2(y, x)
        angles.append(angle)
    sorted_indices = [i for _, i in sorted(zip(angles, face_indices))]
    return sorted_indices

def face_normal(face, vertex_lookup):
    p0 = np.array(vertex_lookup[face[0]])
    p1 = np.array(vertex_lookup[face[1]])
    p2 = np.array(vertex_lookup[face[2]])
    normal = np.cross(p1 - p0, p2 - p0)
    norm = np.linalg.norm(normal)
    if norm == 0:
        return np.array([0,0,0])
    return normal / norm

def get_base_center(vertex_lookup):
    base_points = [v for v in vertex_lookup.values() if abs(v[2]) < 1e-5]
    if base_points:
        return np.mean(base_points, axis=0)
    return np.array([0,0,0])

def ensure_face_orientation(face, vertex_lookup, base_center):
    normal = face_normal(face, vertex_lookup)
    centroid = np.mean([vertex_lookup[v] for v in face], axis=0)
    vec = centroid - base_center
    if np.dot(normal, vec) < 0:
        face = face[::-1]
    return face

def build_rhombus_faces(edges, vertex_lookup, edge_tol=1e-3):
    neighbors = defaultdict(set)
    for a, b in edges:
        neighbors[a].add(b)
        neighbors[b].add(a)

    def edge_length(u, v):
        pu, pv = np.array(vertex_lookup[u]), np.array(vertex_lookup[v])
        return np.linalg.norm(pu - pv)

    result_faces = []
    base_center = get_base_center(vertex_lookup)

    for a in neighbors:
        for b in neighbors[a]:
            if b <= a:
                continue
            for c in neighbors[b]:
                if c in (a,b):
                    continue
                if c not in neighbors:
                    continue
                for d in neighbors[c]:
                    if d in (a,b,c):
                        continue
                    if a in neighbors[d]:
                        lengths = [
                            edge_length(a,b),
                            edge_length(b,c),
                            edge_length(c,d),
                            edge_length(d,a)
                        ]
                        if max(lengths) - min(lengths) < edge_tol:
                            sorted_face = sort_face_vertices([a,b,c,d], vertex_lookup)
                            oriented_face = ensure_face_orientation(sorted_face, vertex_lookup, base_center)
                            if oriented_face not in result_faces:
                                result_faces.append(oriented_face)
    return result_faces

def face_to_triangles(face):
    # face je lista 4 indeksa - podeli na dva trougla
    return [
        [face[0], face[1], face[2]],
        [face[0], face[2], face[3]]
    ]

def build_triangle_adjacency(triangles):
    edge_to_faces = defaultdict(list)
    for i, tri in enumerate(triangles):
        edges = [
            tuple(sorted((tri[0], tri[1]))),
            tuple(sorted((tri[1], tri[2]))),
            tuple(sorted((tri[2], tri[0])))
        ]
        for e in edges:
            edge_to_faces[e].append(i)
    adjacency = defaultdict(set)
    for edge, f_list in edge_to_faces.items():
        if len(f_list) == 2:
            a, b = f_list
            adjacency[a].add(b)
            adjacency[b].add(a)
    return adjacency

def flip_face(face):
    return [face[0], face[2], face[1]]

def calc_normal(v1, v2, v3):
    v1 = np.array(v1)
    v2 = np.array(v2)
    v3 = np.array(v3)
    normal = np.cross(v2 - v1, v3 - v1)
    norm = np.linalg.norm(normal)
    if norm == 0:
        return np.array([0,0,0])
    return normal / norm

def consistent_orientation(vertices, triangles):
    adjacency = build_triangle_adjacency(triangles)
    visited = set()
    queue = deque([0])
    visited.add(0)

    while queue:
        curr = queue.popleft()
        curr_face = triangles[curr]
        curr_normal = calc_normal(vertices[curr_face[0]-1], vertices[curr_face[1]-1], vertices[curr_face[2]-1])

        for neighbor in adjacency[curr]:
            if neighbor in visited:
                continue
            neigh_face = triangles[neighbor]

            shared = set(curr_face) & set(neigh_face)
            if len(shared) != 2:
                continue

            def edge_order(face, edge):
                for i in range(3):
                    e = (face[i], face[(i+1)%3])
                    if set(e) == set(edge):
                        return e
                return None

            shared_edge = tuple(shared)
            curr_edge = edge_order(curr_face, shared_edge)
            neigh_edge = edge_order(neigh_face, shared_edge)

            if curr_edge is None or neigh_edge is None:
                continue

            # Ako su oba u istom smeru, okreni suseda
            if curr_edge == neigh_edge:
                triangles[neighbor] = flip_face(neigh_face)

            visited.add(neighbor)
            queue.append(neighbor)
    return triangles

def export_obj(filename, intersections, edges, faces):
    with open(filename, 'w') as f:
        for p in intersections:
            f.write(f"v {p[0]} {p[1]} {p[2]}\n")
        for a,b in edges:
            f.write(f"l {a} {b}\n")
        for face in faces:
            f.write("f " + " ".join(str(idx) for idx in face) + "\n")
    print(f"✅ Sačuvan OBJ fajl: {filename}")

def unos_broja(prompt, podrazumevano, tip=float):
    while True:
        unos = input(f"{prompt} [{podrazumevano}]: ").strip()
        if unos == "":
            return podrazumevano
        try:
            return tip(unos)
        except ValueError:
            print("⚠️ Neispravan unos, pokušaj ponovo.")

def main():
    print("🌀 GENERATOR SPIRALNE KUPOLE\n")

    n = unos_broja("Unesi broj spirala po smeru", 24, int)
    segs = unos_broja("Unesi broj segmenata po spirali", 24, int)
    d = unos_broja("Unesi prečnik kupole", 4.0)
    h = unos_broja("Unesi visinu kupole", 2.0)

    filename = input("Unesi naziv izlaznog OBJ fajla [helix.obj]: ").strip()
    if filename == "":
        filename = "helix.obj"
    if not filename.endswith(".obj"):
        filename += ".obj"

    tol = 1e-3

    spirals_right = generate_spiral(n, segs, d, h, direction=1)
    spirals_left  = generate_spiral(n, segs, d, h, direction=-1)

    intersections = find_intersections(spirals_right, spirals_left, tol=tol)
    if not intersections:
        print("⚠️ Nema presečnih tačaka!")
        return

    all_spirals = spirals_right + spirals_left
    point_idx, edges = build_graph(intersections, all_spirals, tol=tol)

    # Napravi reverzni lookup: index -> koordinata
    vertex_lookup = {idx: pt for pt, idx in point_idx.items()}

    faces = build_rhombus_faces(edges, vertex_lookup, edge_tol=tol)
    if not faces:
        print("⚠️ Nema pronađenih faces!")
        return

    # Razdvoji faces (četvorke) u trouglove za orijentaciju
    triangles = []
    for face in faces:
        tris = face_to_triangles(face)
        triangles.extend(tris)

    # Ispravi globalnu orijentaciju trouglova
    triangles = consistent_orientation(intersections, triangles)

    # Ponovo spoji trouglove u četvorke za OBJ fajl
    # (Ovde ćemo eksportovati trouglove jer je OBJ standard fleksibilan)
    # Ali ako želiš, možeš grupisati trouglove u četvorke,
    # ili eksportovati trouglove direktno.

    # Eksportuj OBJ sa trouglovima i linijama
    with open(filename, 'w') as f:
        for p in intersections:
            f.write(f"v {p[0]} {p[1]} {p[2]}\n")
        for a,b in edges:
            f.write(f"l {a} {b}\n")
        for tri in triangles:
            f.write("f " + " ".join(str(idx) for idx in tri) + "\n")

    print(f"✅ Sačuvan OBJ fajl sa pravilno orijentisanim trouglovima: {filename}")

if __name__ == "__main__":
    main()

Program obj2ply.py

Opis programa obj2ply.py

Program obj2ply.py služi za konverziju jednostavnih žičanih 3D modela (OBJ format sa tačkama i linijama) u telo sastavljeno od cilindričnih šipki, koje se čuvaju u PLY formatu pogodnom za 3D štampu, vizualizaciju i obradu.

Čemu služi:

• Pretvara linije (l) iz .obj fajla u trodimenzionalne cilindre sa zadatom debljinom (promenljiva RADIUS).
• Svaka linija između dve tačke postaje geometrijski oblik (cilindar) sa površinama.
• Izlaz je .ply fajl sa kompletnom geometrijom šipkaste strukture.

Kako se koristi:

Pokretanje iz komandne linije:

python3 obj2ply.py ime_fajla.obj

Tokom pokretanja programa korisnik bira boju kojom će biti obojen ceo model. Boja se unosi izborom iz ponuđene liste, a zatim se sačuva u PLY fajlu kao RGB vrednosti za svaki vertex.

Program:

1. Učita tačke i ivice iz .obj fajla.
2. Za svaku ivicu napravi cilindar između odgovarajućih tačaka.
3. Sačuva rezultat u .ply fajl sa istim imenom.

Napomena:

• Podržani su samo .obj fajlovi koji sadrže definisane tačke (v) i linije (l).
• Debljina šipki i broj segmenata mogu se podesiti direktno u kodu (RADIUS, CYLINDER_SEGMENTS).

Kod programa obj2ply.py:

# The MIT License (MIT)
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovim se omogućava bilo kome da koristi, kopira, menja, spaja, objavljuje,
# distribuira, daje podlicencu i/ili prodaje kopije ovog softverskog programa,
# uz uslov da u svim kopijama ili značajnim delovima softverskog programa bude
# uključena sledeća obavest:
#
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovaj softverski program je pružen "takav kakav jeste", bez bilo kakvih garancija,
# izričitih ili impliciranih, uključujući, ali ne ograničavajući se na, garancije o
# prikladnosti za prodaju ili pogodnosti za određenu svrhu. U svakom slučaju, autori
# ili nosioci prava nisu odgovorni za bilo kakvu štetu ili druge obaveze koje mogu nastati
# usled upotrebe ovog softverskog programa.
# Naziv programa: KONVERTOR IZ OBJ U PLY



import numpy as np
import sys
from pathlib import Path

RADIUS = 0.01
CYLINDER_SEGMENTS = 16

# Definiši dostupne boje kao RGB (0-255)
BOJE = {
    1: ("bela", (255, 255, 255)),
    2: ("crvena", (255, 0, 0)),
    3: ("zelena", (0, 255, 0)),
    4: ("plava", (0, 0, 255)),
    5: ("žuta", (255, 255, 0)),
    6: ("ljubičasta", (128, 0, 128)),
    7: ("narandžasta", (255, 165, 0)),
    8: ("tirkizna", (64, 224, 208)),
    9: ("siva", (128, 128, 128)),
    10: ("crna", (0, 0, 0)),
}


def prikazi_meni_i_uzmi_boju():
    print("Izaberite boju modela:")
    for broj, (ime, rgb) in sorted(BOJE.items()):
        print(f"{broj}. {ime} (RGB: {rgb})")
    while True:
        try:
            izbor = int(input("Unesite broj boje: "))
            if izbor in BOJE:
                return BOJE[izbor][1]
            else:
                print("Nepoznat broj boje, pokušajte ponovo.")
        except ValueError:
            print("Molimo unesite ceo broj.")


def ucitaj_obj(path):
    vertices = []
    edges = []
    with open(path, "r") as f:
        for line in f:
            if line.startswith("v "):
                _, x, y, z = line.strip().split()
                vertices.append(np.array([float(x), float(y), float(z)]))
            elif line.startswith("l "):
                parts = line.strip().split()
                edges.append((int(parts[1]) - 1, int(parts[2]) - 1))
    return vertices, edges


def napravi_cilindar(p1, p2, radius, segments=16):
    v = p2 - p1
    length = np.linalg.norm(v)
    if length < 1e-8:
        return [], []

    axis = v / length

    if abs(axis[0]) < 0.001 and abs(axis[1]) < 0.001:
        ortho = np.array([1, 0, 0])
    else:
        ortho = np.array([0, 0, 1])

    n1 = np.cross(axis, ortho)
    n1 /= np.linalg.norm(n1)
    n2 = np.cross(axis, n1)
    n2 /= np.linalg.norm(n2)

    circle_p1 = []
    circle_p2 = []
    for i in range(segments):
        theta = 2 * np.pi * i / segments
        dir_vec = np.cos(theta) * n1 + np.sin(theta) * n2
        circle_p1.append(p1 + radius * dir_vec)
        circle_p2.append(p2 + radius * dir_vec)

    vertices = circle_p1 + circle_p2
    faces = []

    for i in range(segments):
        i_next = (i + 1) % segments
        faces.append((i, i_next, i_next + segments))
        faces.append((i, i_next + segments, i + segments))

    return vertices, faces


def sacuvaj_ply(verts, faces, filename, boja):
    r, g, b = boja
    with open(filename, "w") as f:
        f.write("ply\n")
        f.write("format ascii 1.0\n")
        f.write(f"element vertex {len(verts)}\n")
        f.write("property float x\nproperty float y\nproperty float z\n")
        # Dodajemo RGB atribute
        f.write("property uchar red\nproperty uchar green\nproperty uchar blue\n")
        f.write(f"element face {len(faces)}\n")
        f.write("property list uchar int vertex_indices\n")
        f.write("end_header\n")

        for v in verts:
            f.write(f"{v[0]} {v[1]} {v[2]} {r} {g} {b}\n")

        for face in faces:
            f.write(f"3 {face[0]} {face[1]} {face[2]}\n")


def main():
    if len(sys.argv) != 2:
        print("Upotreba: python3 obj2ply.py ulazni_fajl.obj")
        return

    input_path = Path(sys.argv[1])
    if not input_path.exists():
        print(f"Fajl ne postoji: {input_path}")
        return

    boja = prikazi_meni_i_uzmi_boju()

    output_path = input_path.with_suffix(".ply")

    vertices, edges = ucitaj_obj(input_path)
    print(f"Učitano {len(vertices)} tačaka i {len(edges)} ivica iz {input_path}")

    sve_verteksi = []
    sve_face = []
    offset = 0

    for i1, i2 in edges:
        p1 = vertices[i1]
        p2 = vertices[i2]

        verts_cil, faces_cil = napravi_cilindar(p1, p2, RADIUS, CYLINDER_SEGMENTS)

        sve_verteksi.extend(verts_cil)
        for f in faces_cil:
            sve_face.append((f[0] + offset, f[1] + offset, f[2] + offset))

        offset += len(verts_cil)

    sacuvaj_ply(sve_verteksi, sve_face, output_path, boja)
    print(f"Ply fajl sa šipkama sačuvan kao: {output_path}")


if __name__ == "__main__":
    main()

Program obj2dxf.py

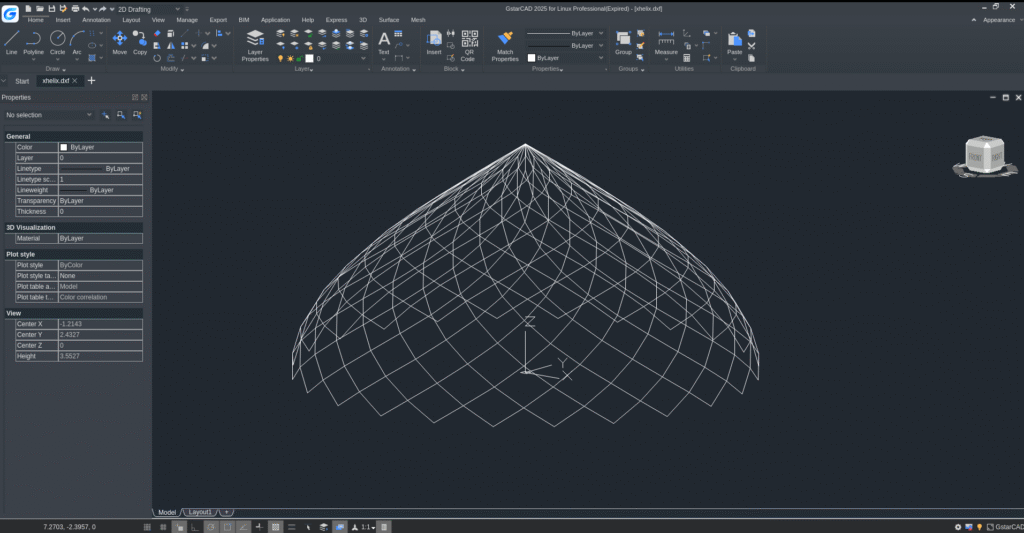
Opis programa obj2dxf.py

Program obj2dxf.py služi za konvertovanje jednostavnih 3D žičanih modela iz formata OBJ (sa tačkama i linijama) u 2D/3D DXF format, koji se često koristi u CAD softverima.

Čemu služi:

• Učitava koordinate tačaka i linija iz .obj fajla.
• Kreira DXF fajl gde su linije modela rekonstruisane kao DXF entiteti.
• Omogućava dalju CAD obradu i prikaz u programima koji podržavaju DXF.

Kako se koristi:

Pokrenite program komandno sa:

python3 obj2dxf.py ime_fajla.obj

Program:

1. Učita .obj fajl sa definisanim vrhovima i linijama.
2. Sačuva DXF fajl sa istim imenom i ekstenzijom .dxf.

Napomena:

• Podržani su samo .obj fajlovi sa tačkama (v) i linijama (l).
• Rezultat je DXF fajl u verziji R2010.

Programski kod obj2dxf.py

# The MIT License (MIT)
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovim se omogućava bilo kome da koristi, kopira, menja, spaja, objavljuje,
# distribuira, daje podlicencu i/ili prodaje kopije ovog softverskog programa,
# uz uslov da u svim kopijama ili značajnim delovima softverskog programa bude
# uključena sledeća obavest:
#
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovaj softverski program je pružen "takav kakav jeste", bez bilo kakvih garancija,
# izričitih ili impliciranih, uključujući, ali ne ograničavajući se na, garancije o
# prikladnosti za prodaju ili pogodnosti za određenu svrhu. U svakom slučaju, autori
# ili nosioci prava nisu odgovorni za bilo kakvu štetu ili druge obaveze koje mogu nastati
# usled upotrebe ovog softverskog programa.
# Naziv programa: KONVERTOR IZ OBJ U DXF


import ezdxf
import sys
from pathlib import Path


def read_obj_vertices_and_lines(filename):
    vertices = []
    lines = []

    with open(filename, 'r') as f:
        for line in f:
            if line.startswith('v '):
                parts = line.strip().split()
                x, y, z = float(parts[1]), float(parts[2]), float(parts[3])
                vertices.append((x, y, z))
            elif line.startswith('l '):
                parts = line.strip().split()
                i1 = int(parts[1]) - 1
                i2 = int(parts[2]) - 1
                lines.append((i1, i2))

    return vertices, lines


def obj_to_dxf(obj_file, dxf_file):
    vertices, lines = read_obj_vertices_and_lines(obj_file)
    doc = ezdxf.new(dxfversion="R2010")
    msp = doc.modelspace()

    for i1, i2 in lines:
        p1 = vertices[i1]
        p2 = vertices[i2]
        msp.add_line(p1, p2)

    doc.saveas(dxf_file)
    print(f"✅ Sačuvan: {dxf_file}")


def main():
    if len(sys.argv) != 2:
        print("Upotreba: python3 obj2dxf.py ulazni_fajl.obj")
        return

    input_path = Path(sys.argv[1])
    if not input_path.exists():
        print(f"❌ Fajl ne postoji: {input_path}")
        return

    output_path = input_path.with_suffix('.dxf')
    obj_to_dxf(str(input_path), str(output_path))


if __name__ == "__main__":
    main()

Program obj2stl.py

Opis programa obj2stl.py

Ovaj program služi za konverziju 3D modela iz OBJ formata u STL format. Učitava geometriju iz OBJ fajla, uključujući verteks (tačke) i face (površinske trouglove), a zatim generiše odgovarajući ASCII STL fajl sa izračunatim normalama za svaki trougao. Program podržava i objekte sa licima koja imaju više od tri verteksa tako što ih automatski trianguliše.

Kako se koristi

1. Pokreni program iz komandne linije, navodeći putanju do OBJ fajla:
2. python3 obj2stl.py model.obj
3. Program će učitati OBJ fajl, konvertovati ga u STL format i sačuvati izlazni fajl sa istim imenom, ali sa .stl ekstenzijom u istom direktorijumu.
4. U slučaju problema (npr. nepostojeći fajl ili nepravilni podaci), program će prikazati odgovarajuću poruku.

Programski kod obj2stl.py:

# The MIT License (MIT)
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovim se omogućava bilo kome da koristi, kopira, menja, spaja, objavljuje,
# distribuira, daje podlicencu i/ili prodaje kopije ovog softverskog programa,
# uz uslov da u svim kopijama ili značajnim delovima softverskog programa bude
# uključena sledeća obavest:
#
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovaj softverski program je pružen "takav kakav jeste", bez bilo kakvih garancija,
# izričitih ili impliciranih, uključujući, ali ne ograničavajući se na, garancije o
# prikladnosti za prodaju ili pogodnosti za određenu svrhu. U svakom slučaju, autori
# ili nosioci prava nisu odgovorni za bilo kakvu štetu ili druge obaveze koje mogu nastati
# usled upotrebe ovog softverskog programa.
# Naziv programa: KONVERTOR IZ OBJ U STL


import sys
import os

def read_obj(filename):
    vertices = []
    faces = []
    with open(filename, 'r') as f:
        for line in f:
            if line.startswith('v '):
                parts = line.strip().split()
                vertex = list(map(float, parts[1:4]))
                vertices.append(vertex)
            elif line.startswith('f '):
                parts = line.strip().split()
                # Faces mogu biti u formatu f v1 v2 v3 ili sa teksturama/normalama: f v1/vt1/vn1 ...
                face = []
                for part in parts[1:]:
                    idx = part.split('/')[0]  # uzimamo samo indeks vrha
                    face.append(int(idx))
                # Ako je lice sa više od 3 vrha (npr. četvorka), trijažemo na trouglove
                if len(face) == 3:
                    faces.append(face)
                elif len(face) > 3:
                    # triangulacija fan metodom
                    for i in range(1, len(face)-1):
                        faces.append([face[0], face[i], face[i+1]])
    return vertices, faces

def write_stl(filename, vertices, faces):
    with open(filename, 'w') as f:
        f.write("solid converted\n")
        for face in faces:
            v1 = vertices[face[0]-1]
            v2 = vertices[face[1]-1]
            v3 = vertices[face[2]-1]
            # Izračun normalnog vektora
            normal = calc_normal(v1, v2, v3)
            f.write(f"  facet normal {normal[0]} {normal[1]} {normal[2]}\n")
            f.write("    outer loop\n")
            f.write(f"      vertex {v1[0]} {v1[1]} {v1[2]}\n")
            f.write(f"      vertex {v2[0]} {v2[1]} {v2[2]}\n")
            f.write(f"      vertex {v3[0]} {v3[1]} {v3[2]}\n")
            f.write("    endloop\n")
            f.write("  endfacet\n")
        f.write("endsolid converted\n")

def calc_normal(v1, v2, v3):
    import numpy as np
    v1 = np.array(v1)
    v2 = np.array(v2)
    v3 = np.array(v3)
    normal = np.cross(v2 - v1, v3 - v1)
    norm = np.linalg.norm(normal)
    if norm == 0:
        return (0.0, 0.0, 0.0)
    return normal / norm

def main():
    if len(sys.argv) < 2:
        print("Upotreba: python3 obj2stl.py naziv_fajla.obj")
        sys.exit(1)

    input_file = sys.argv[1]
    if not input_file.lower().endswith('.obj'):
        print("Ulazni fajl mora biti .obj")
        sys.exit(1)

    vertices, faces = read_obj(input_file)
    if not vertices or not faces:
        print("Obj fajl nema vertekse ili faces.")
        sys.exit(1)

    output_file = os.path.splitext(input_file)[0] + '.stl'
    write_stl(output_file, vertices, faces)
    print(f"✅ STL fajl sačuvan kao: {output_file}")

if __name__ == "__main__":
    main()

Kombinacija STL i PLY

Program obj2stat.py

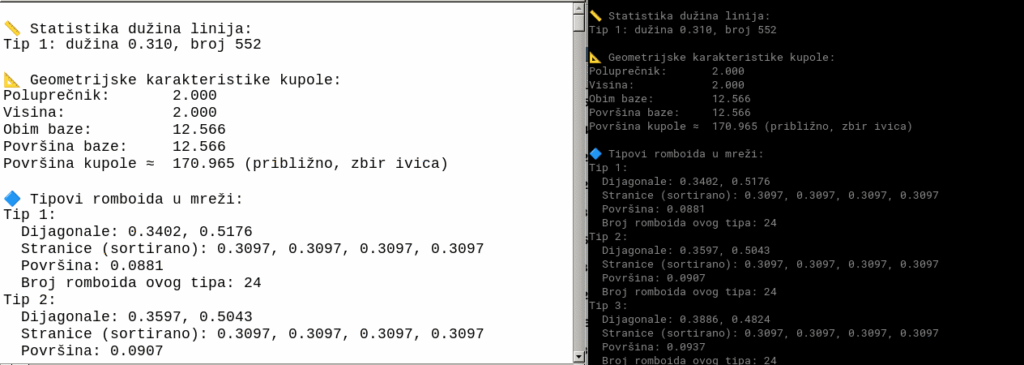
Opis programa obj2stat.py

Program obj2stat.py služi za analizu 3D žičanih modela kupola ili sličnih struktura definisanih u OBJ formatu (tačke i linije). Cilj je da se izračunaju statistike o dužinama ivica, osnovne geometrijske karakteristike kupole, kao i da se prepoznaju i analiziraju romboidni paneli (četvorka tačaka koje formiraju romboid).

Funkcionalnosti:

• Učitava vrhove i linije iz .obj fajla.
• Grupira linije prema dužini i prikazuje koliko ima segmenata po tipu dužine.
• Izračunava:
  • poluprečnik kupole,
  • visinu,
  • obim baze,
  • površinu baze,
  • približnu površinu kupole (zbir ivica).
• Detektuje romboidne elemente u mreži i analizira njihove dimenzije (dužine stranica, dijagonale, površine).
• Generiše tekstualni izveštaj sa svim statističkim podacima.

Kako se koristi:

Pokrenite program komandno:

python3 obj2stat.py ulazni_fajl.obj

Program automatski kreira izveštaj u tekstualnom fajlu sa dodatkom _izvestaj.txt u imenu, koji sadrži detaljne analize i statistike.

Priloženi programski kod za obj2stat.py

NIJE PROVEREN!

Nema garancije za tačnost rezultata:

# The MIT License (MIT)
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovim se omogućava bilo kome da koristi, kopira, menja, spaja, objavljuje,
# distribuira, daje podlicencu i/ili prodaje kopije ovog softverskog programa,
# uz uslov da u svim kopijama ili značajnim delovima softverskog programa bude
# uključena sledeća obavest:
#
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovaj softverski program je pružen "takav kakav jeste", bez bilo kakvih garancija,
# izričitih ili impliciranih, uključujući, ali ne ograničavajući se na, garancije o
# prikladnosti za prodaju ili pogodnosti za određenu svrhu. U svakom slučaju, autori
# ili nosioci prava nisu odgovorni za bilo kakvu štetu ili druge obaveze koje mogu nastati
# usled upotrebe ovog softverskog programa.
# Naziv programa: ANALIZA I STATISTIKA KUPOLE

import numpy as np
from collections import defaultdict
from math import pi
from pathlib import Path
import sys

def read_obj_vertices_and_lines(filename):
    vertices = []
    lines = []

    with open(filename, 'r') as f:
        for line in f:
            if line.startswith('v '):
                parts = line.strip().split()
                vertices.append([float(parts[1]), float(parts[2]), float(parts[3])])
            elif line.startswith('l '):
                parts = line.strip().split()
                i1, i2 = int(parts[1]) - 1, int(parts[2]) - 1
                lines.append((i1, i2))

    return np.array(vertices), lines

def group_lines_by_length(vertices, lines, tolerance=1e-3):
    length_groups = defaultdict(list)
    for i1, i2 in lines:
        p1 = vertices[i1]
        p2 = vertices[i2]
        length = np.linalg.norm(p1 - p2)
        key = round(length / tolerance) * tolerance
        length_groups[key].append((i1, i2))
    return dict(sorted(length_groups.items()))

def print_line_statistics(length_groups, out):
    print_and_write(out, "\n📏 Statistika dužina linija:")
    for i, (length, lines) in enumerate(length_groups.items(), start=1):
        print_and_write(out, f"Tip {i}: dužina {length:.3f}, broj {len(lines)}")

def compute_dome_geometry(vertices, lines):
    radii = np.linalg.norm(vertices[:, :2], axis=1)
    radius = np.max(radii)
    z_min = np.min(vertices[:, 2])
    z_max = np.max(vertices[:, 2])
    height = z_max - z_min
    circumference = 2 * pi * radius
    base_area = pi * radius**2
    surface_approx = sum(np.linalg.norm(vertices[i1] - vertices[i2]) for i1, i2 in lines)
    return radius, height, circumference, base_area, surface_approx

def find_rhomboids(vertices, lines, tolerance=1e-5):
    adjacency = defaultdict(set)
    for i1, i2 in lines:
        adjacency[i1].add(i2)
        adjacency[i2].add(i1)

    rhomboids = []
    visited = set()

    for A in range(len(vertices)):
        for B in adjacency[A]:
            for C in adjacency[B]:
                if C == A:
                    continue
                for D in adjacency[C]:
                    if D == B or D == A:
                        continue
                    if D in adjacency[A]:
                        quad = tuple(sorted([A, B, C, D]))
                        if quad in visited:
                            continue
                        visited.add(quad)
                        rhomboids.append([A, B, C, D])
    return rhomboids

def edge_length(vertices, i1, i2):
    return np.linalg.norm(vertices[i1] - vertices[i2])

def rhomboid_area(vertices, quad):
    A, B, C, D = quad
    AC = vertices[C] - vertices[A]
    BD = vertices[D] - vertices[B]
    return 0.5 * np.linalg.norm(np.cross(AC, BD))

def analyze_rhomboids(vertices, rhomboids, out, tolerance=1e-3):
    rhomb_types = {}
    rhomb_counts = defaultdict(int)

    def approx_equal_tuple(t1, t2):
        return all(abs(x - y) < tolerance for x, y in zip(t1, t2))

    for quad in rhomboids:
        A, B, C, D = quad
        sides = (
            edge_length(vertices, A, B),
            edge_length(vertices, B, C),
            edge_length(vertices, C, D),
            edge_length(vertices, D, A),
        )
        diagonals = (
            edge_length(vertices, A, C),
            edge_length(vertices, B, D)
        )
        sides_sorted = tuple(sorted(sides))
        diagonals_sorted = tuple(sorted(diagonals))
        key = (diagonals_sorted, sides_sorted)

        found_key = None
        for k in rhomb_types.keys():
            if approx_equal_tuple(k[0], key[0]) and approx_equal_tuple(k[1], key[1]):
                found_key = k
                break

        if found_key is None:
            rhomb_types[key] = quad
            rhomb_counts[key] = 1
        else:
            rhomb_counts[found_key] += 1

    print_and_write(out, "\n🔷 Tipovi romboida u mreži:")
    for i, (key, quad) in enumerate(rhomb_types.items(), start=1):
        diagonals_sorted, sides_sorted = key
        area = rhomboid_area(vertices, quad)
        print_and_write(out, f"Tip {i}:")
        print_and_write(out, f"  Dijagonale: {diagonals_sorted[0]:.4f}, {diagonals_sorted[1]:.4f}")
        print_and_write(out, f"  Stranice (sortirano): {sides_sorted[0]:.4f}, {sides_sorted[1]:.4f}, {sides_sorted[2]:.4f}, {sides_sorted[3]:.4f}")
        print_and_write(out, f"  Površina: {area:.4f}")
        print_and_write(out, f"  Broj romboida ovog tipa: {rhomb_counts[key]}")

def print_and_write(out, text):
    print(text)
    out.write(text + "\n")

def main():
    if len(sys.argv) != 2:
        print("Upotreba: python3 analiza.py ulazni_fajl.obj")
        return

    input_path = Path(sys.argv[1])
    if not input_path.exists():
        print(f"❌ Fajl ne postoji: {input_path}")
        return

    output_txt = input_path.with_stem(input_path.stem + "_izvestaj").with_suffix(".txt")

    with open(output_txt, "w") as out:
        vertices, lines = read_obj_vertices_and_lines(str(input_path))

        length_groups = group_lines_by_length(vertices, lines, tolerance=1e-3)
        print_line_statistics(length_groups, out)

        radius, height, circumference, base_area, surface_approx = compute_dome_geometry(vertices, lines)

        print_and_write(out, "\n📐 Geometrijske karakteristike kupole:")
        print_and_write(out, f"Poluprečnik:       {radius:.3f}")
        print_and_write(out, f"Visina:            {height:.3f}")
        print_and_write(out, f"Obim baze:         {circumference:.3f}")
        print_and_write(out, f"Površina baze:     {base_area:.3f}")
        print_and_write(out, f"Površina kupole ≈  {surface_approx:.3f} (približno, zbir ivica)")

        rhomboids = find_rhomboids(vertices, lines)
        analyze_rhomboids(vertices, rhomboids, out, tolerance=1e-3)

    print(f"\n📝 Izveštaj sačuvan u: {output_txt}")

if __name__ == "__main__":
    main()

Linkovi:

Reference:

Matematički modeli i teorija

1. „The Mathematics of Zome“ – Tom Davis
   Izuzetno detaljan papir (PDF) koji prikazuje kako izračunati dužine šipki u Zome sistemu i kako se čvorišta međusobno povezuju
   https://www.yumpu.com/en/document/view/25868597/zome-patterns-home-page-tom-davis
2. „Spinning Circles and Parametric Approach“ – SimplyDifferently.org
   Web članak objašnjava dve metode generisanja helix Zome geometrije: korišćenjem uvijenih kružnica i parametrskog pristupa
   https://www.simplydifferently.org/Helix_Zome
3. Zometool Manual 2.3 Detaljni PDF vodič sa uvodom u strukturu boja i simetrije Zome sistema (2-, 3‑ i 5‑fold modeli), te primene u geometriji i edukaciji: https://www.researchgate.net/publication/344594402_From_Zoom_Organization_to_Zome_Configuration_and_Dynamics_Integrating_the_doughnut_helix_and_pineapple_models_towards_global_strategic_coherence

Kontekst i primena

4. https://www.gradnja.rs/ove-montazne-modularne-kupole-po-projektu-domacih-arhitekata-izvodice-se-u-sad
5. Laetus in Praesens – o “Zonoedrima i Zome konstrukcijama”
   Analiza spirala i helix formi unutar Zome struktura, spominje zlati rez i geometriju zamishljenog sustava: https://www.laetusinpraesens.org/pdfs/2020s/zoomzome_2020.pdf