Pripremite se za putovanje izvan granica poznatih dimenzija — tamo gde svetlost projektuje senke višedimenzionalnih svetova u našu trodimenzionalnu realnost.
U svakodnevnom iskustvu živimo u svetu tri dimenzije — dužine, širine i visine. Kada želimo da predstavimo trodimenzionalni objekat na dvodimenzionalnoj površini (poput papira ili ekrana), koristimo perspektivu i senčenje da bismo stvorili iluziju dubine. Ali šta se dešava kada pokušamo da zamislimo četvrtu, petu ili čak šestu prostornu dimenziju?
Ovaj članak je uvod u seriju interaktivnih programa koji omogućavaju upravo to — istraživanje i vizuelizaciju višedimenzionalnih kocki (tzv. hiperkocki) kroz njihove senke projektovane na 2D ravan. Ovi programi vam omogućavaju da, pomoću tastature, rotirate nevidljive strukture u višedimenzionalnom prostoru, dok na ekranu posmatrate njihove senke — nalik senkama koje trodimenzionalni objekti bacaju na zid u igri svetlosti.
Šta je hiperkocka?
Hiperkocka je generalizacija kocke u višim dimenzijama. Terminologija se razvija sa dimenzijama:
- Kvadrat je 2D kocka.
- Kocka je 3D kocka.
- Teserakt je 4D kocka.
- Penterakt je 5D kocka.
- Hekserakt je 6D kocka.
Iako ne možemo direktno “videti” objekte u više od tri dimenzije, matematika nam omogućava da ih precizno opišemo i manipulišemo njima. Svaka hiperkocka ima definisane temene, ivice, plohe i njihove višedimenzionalne analogije, a zahvaljujući računarima, možemo ih projektovati u dve dimenzije i analizirati njihove “senke”.
Vizuelizacija pomoću senki
Baš kao što trodimenzionalna kocka baca dvodimenzionalnu senku kada se osvetli, višedimenzionalna kocka može da “baci” svoju senku u nižim dimenzijama. Programi koje ćemo koristiti funkcionišu upravo tako:
- Generišu temena i ivice višedimenzionalnih kocki.
- Osvetljavaju ih iz određene tačke u prostoru.
- Projektuju “senke” ivica i čvorišta na sve moguće 2D ravni.
- Omogućavaju rotaciju hiperkocke u njenom višedimenzionalnom prostoru, čime se menja oblik senke.
Zašto ovo radimo?
Ova tehnika nije samo vizuelno fascinantna — ona je i konceptualno korisna. Proučavanje višedimenzionalnih prostora igra ključnu ulogu u teorijskoj fizici, kompjuterskoj grafici, mašinskom učenju i matematici. Razumevanje kako se ponašaju objekti u višim dimenzijama razvija intuiciju koja prevazilazi svakodnevno iskustvo.
Šta sledi?
U narednim tekstovima i pratećim Python programima, upoznaćemo se sa:
- Vizuelizacijom 4D teserakta i njegovih 6 projekcija na 2D ravni.
- Vizualizacijom 5D penterakta i njegovih 10 projekcija.
- Vizualizacijom 6D hekserakta i čak 15 mogućih senki.
Svi programi su interaktivni — pomoću tastature možete “rotirati” hiperkocku i pratiti kako se menjaju senke koje padaju na dvodimenzionalnu površinu. Na taj način, prostor viših dimenzija prestaje da bude apstraktna ideja i počinje da poprima konkretnu vizuelnu formu.
Vizuelizacija 4D teserakta i njegovih 6 projekcija na 2D ravni
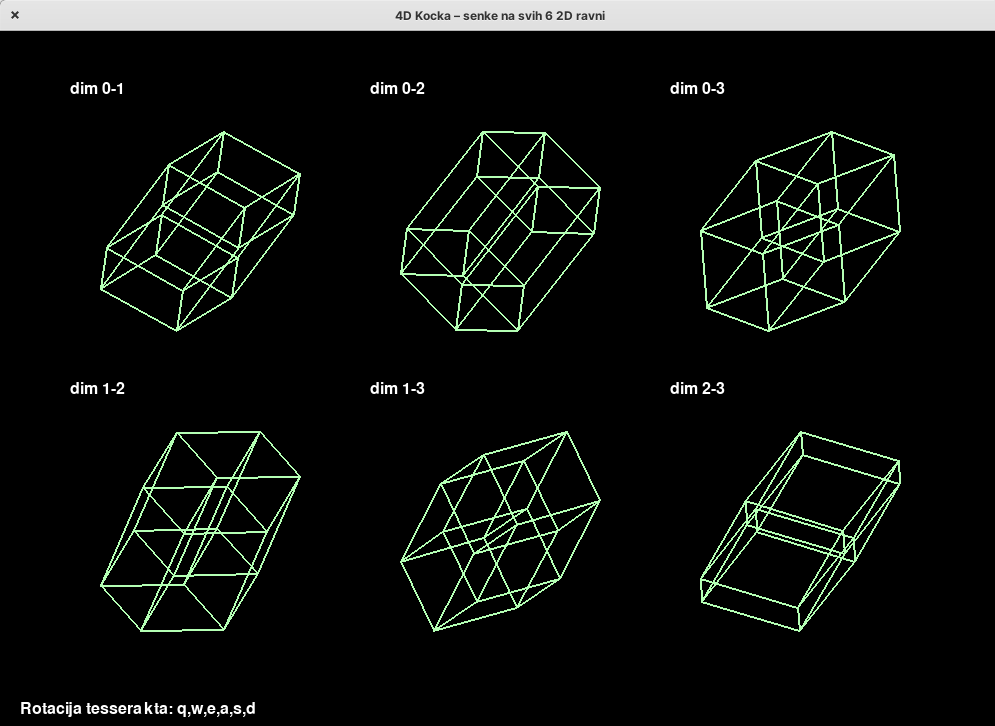
Instalacija svih potrebnih zavisnosti:
python3 -m pip install numpy pygame
Programski kod za teserakt.py
#teserakt.py
# Instalacija potrebnih zavisnosti: python3 -m pip install numpy pygame
import numpy as np
import pygame
import sys
from itertools import combinations
# Dimenzija tesserakta
DIM = 4
# Generiši temena tesserakta
def generate_hypercube(dim):
return np.array(list(np.ndindex(*(2,) * dim)))
# Generiši ivice – tačke koje se razlikuju u tačno jednoj koordinati
def generate_edges(vertices):
edges = []
for i in range(len(vertices)):
for j in range(i + 1, len(vertices)):
if np.sum(np.abs(vertices[i] - vertices[j])) == 1:
edges.append((i, j))
return edges
# Rotacija u ravni (i, j) za ugao theta
def rotate(points, i, j, theta):
rot = np.identity(DIM)
c, s = np.cos(theta), np.sin(theta)
rot[[i, i, j, j], [i, j, i, j]] = c, -s, s, c
return points @ rot
# Projekcija senke na 2D ravan (dim_i, dim_j)
def project_shadow(points, light_dir, dim_i, dim_j):
light_dir = light_dir / np.linalg.norm(light_dir)
projections = points - (points @ light_dir[:, None]) * light_dir
return projections[:, [dim_i, dim_j]]
# Inicijalizuj temena i ivice
vertices = generate_hypercube(DIM)
edges = generate_edges(vertices)
# Sve 2D ravni (0,1), (0,2), ..., (2,3)
projection_planes = list(combinations(range(DIM), 2)) # 6 ravni
# Početni pravac svetlosti
light_dir = np.ones(DIM)
# Rotacione ravni i tasteri
rotation_planes = {
pygame.K_q: (0, 1),
pygame.K_w: (0, 2),
pygame.K_e: (0, 3),
pygame.K_a: (1, 2),
pygame.K_s: (1, 3),
pygame.K_d: (2, 3),
}
theta = 0.01 # ugao rotacije
# Pygame setup
pygame.init()
screen = pygame.display.set_mode((1000, 700))
pygame.display.set_caption("4D Kocka – senke na svih 6 2D ravni")
clock = pygame.time.Clock()
font = pygame.font.SysFont(None, 24)
def draw_text(surface, text, pos, color=(255, 255, 255)):
img = font.render(text, True, color)
surface.blit(img, pos)
def main():
global vertices
running = True
while running:
screen.fill((0, 0, 0))
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
# Rotacija po tasterima
keys = pygame.key.get_pressed()
for key in rotation_planes:
if keys[key]:
i, j = rotation_planes[key]
vertices = rotate(vertices, i, j, theta)
# Crtanje svih 2D projekcija
for idx, (i, j) in enumerate(projection_planes):
proj = project_shadow(vertices, light_dir, i, j)
min_p, max_p = proj.min(axis=0), proj.max(axis=0)
scale = 200
margin_x, margin_y = 300 * (idx % 3), 300 * (idx // 3)
offset = np.array([100 + margin_x, 100 + margin_y])
norm_proj = (proj - min_p) / (max_p - min_p + 1e-5) * scale + offset
# Crtanje ivica
for e0, e1 in edges:
p1, p2 = norm_proj[e0], norm_proj[e1]
pygame.draw.line(screen, (180, 255, 180), p1, p2, 2)
draw_text(screen, f"dim {i}-{j}", (offset[0] - 30, offset[1] - 50))
draw_text(screen, "Rotacija tesserakta: q,w,e,a,s,d", (20, 670))
pygame.display.flip()
clock.tick(30)
pygame.quit()
sys.exit()
main()
Vizualizacija 5D penterakta i njegovih 10 projekcija na 2D ravni
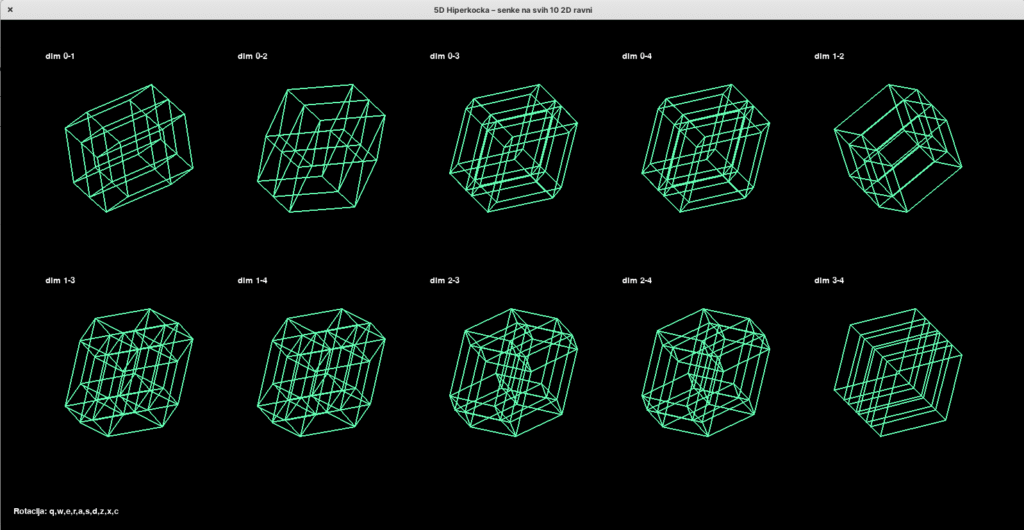
Instalacija svih potrebnih zavisnosti:
python3 -m pip install numpy pygame
Programski kod za penterakt.py
#penterakt.py
# Instalacija potrebnih zavisnosti: python3 -m pip install numpy pygame
import numpy as np
import pygame
import sys
from itertools import combinations
# Dimenzija hiperkocke
DIM = 5
# Generisanje temena 5D hiperkocke (32 tačke)
def generate_hypercube(dim):
return np.array(list(map(list, np.ndindex(*(2,) * dim))))
# Generisanje ivica: povezane su tačke koje se razlikuju u tačno jednoj koordinati
def generate_edges(vertices):
edges = []
for i in range(len(vertices)):
for j in range(i + 1, len(vertices)):
if np.sum(np.abs(vertices[i] - vertices[j])) == 1:
edges.append((i, j))
return edges
# Rotacija u ravni (i, j) za ugao theta
def rotate(points, i, j, theta):
rot = np.identity(DIM)
c, s = np.cos(theta), np.sin(theta)
rot[[i, i, j, j], [i, j, i, j]] = c, -s, s, c
return points @ rot
# Projekcija senke u ravnima dim_i-dim_j (iz pravca svetla)
def project_shadow(points, light_dir, dim_i, dim_j):
light_dir = light_dir / np.linalg.norm(light_dir)
projections = points - (points @ light_dir[:, None]) * light_dir
return projections[:, [dim_i, dim_j]]
# Inicijalizacija temena i ivica
vertices = generate_hypercube(DIM)
edges = generate_edges(vertices)
# Definisanje svih 2D ravni za 5D prostor (10 ravni)
projection_planes = list(combinations(range(DIM), 2)) # (0,1), (0,2), ..., (3,4)
# Inicijalni pravac svetlosti
light_dir = np.ones(DIM)
# Rotacione ravni i odgovarajući tasteri
rotation_planes = {
pygame.K_q: (0, 1),
pygame.K_w: (0, 2),
pygame.K_e: (0, 3),
pygame.K_r: (0, 4),
pygame.K_a: (1, 2),
pygame.K_s: (1, 3),
pygame.K_d: (1, 4),
pygame.K_v: (2, 3),
pygame.K_x: (2, 4),
pygame.K_c: (3, 4),
}
theta = 0.1 # ugao rotacije
# Pygame setup
pygame.init()
screen = pygame.display.set_mode((1600, 800))
pygame.display.set_caption("5D Hiperkocka – senke na svih 10 2D ravni")
clock = pygame.time.Clock()
font = pygame.font.SysFont(None, 20)
def draw_text(surface, text, pos, color=(255, 255, 255)):
img = font.render(text, True, color)
surface.blit(img, pos)
def main():
global vertices
running = True
while running:
screen.fill((0, 0, 0))
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
keys = pygame.key.get_pressed()
for key in rotation_planes:
if keys[key]:
i, j = rotation_planes[key]
vertices = rotate(vertices, i, j, theta)
# Crtanje svih 10 projekcija
for idx, (i, j) in enumerate(projection_planes):
proj = project_shadow(vertices, light_dir, i, j)
min_p, max_p = proj.min(axis=0), proj.max(axis=0)
scale = 200
margin_x, margin_y = 300 * (idx % 5), 350 * (idx // 5)
offset = np.array([100 + margin_x, 100 + margin_y])
norm_proj = (proj - min_p) / (max_p - min_p + 1e-5) * scale + offset
# Crtanje ivica
for e0, e1 in edges:
p1 = norm_proj[e0]
p2 = norm_proj[e1]
pygame.draw.line(screen, (100, 255, 180), p1, p2, 2)
draw_text(screen, f"dim {i}-{j}", (offset[0] - 30, offset[1] - 50))
draw_text(screen, "Rotacija: q,w,e,r,a,s,d,z,x,c", (20, 760))
pygame.display.flip()
clock.tick(30)
pygame.quit()
sys.exit()
main()
Vizualizacija 6D hekserakta i njegovih 15 projekcija na 2D ravni

Instalacija svih potrebnih zavisnosti:
python3 -m pip install numpy matplotlib pygame
Programski kod za hekserakt.py
#hekserakt.py
# Instalacija potrebnih zavisnosti: python3 -m pip install numpy matplotlib pygame
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from itertools import combinations
import pygame
import sys
# Dimenzije
DIM = 6
# Generisanje temena 6D hiperkocke (64 tačke)
def generate_hypercube(dim):
return np.array(list(map(list, np.ndindex(*(2,) * dim))))
# Generisanje ivica: povezane su tačke koje se razlikuju u tačno jednoj koordinati
def generate_edges(vertices):
edges = []
for i in range(len(vertices)):
for j in range(i + 1, len(vertices)):
if np.sum(np.abs(vertices[i] - vertices[j])) == 1:
edges.append((i, j))
return edges
# Rotacija u ravni (i, j) za ugao theta
def rotate(points, i, j, theta):
rot = np.identity(DIM)
c, s = np.cos(theta), np.sin(theta)
rot[[i, i, j, j], [i, j, i, j]] = c, -s, s, c
return points @ rot
# Projekcija senke u ravnima dim_i-dim_j (iz pravca svetla)
def project_shadow(points, light_dir, dim_i, dim_j):
light_dir = light_dir / np.linalg.norm(light_dir)
projections = points - (points @ light_dir[:, None]) * light_dir
return projections[:, [dim_i, dim_j]]
# Inicijalizacija
vertices = generate_hypercube(DIM)
edges = generate_edges(vertices)
# Definisanje svih 15 ravni dimenzija
projection_planes = list(combinations(range(DIM), 2)) # (0,1), (0,2), ..., (4,5)
# Inicijalni pravac svetlosti
light_dir = np.ones(DIM)
# Rotacione ravni i odgovarajući tasteri
rotation_planes = {
pygame.K_q: (0, 1),
pygame.K_w: (0, 2),
pygame.K_e: (0, 3),
pygame.K_r: (0, 4),
pygame.K_t: (0, 5),
pygame.K_a: (1, 2),
pygame.K_s: (1, 3),
pygame.K_d: (1, 4),
pygame.K_f: (1, 5),
pygame.K_z: (2, 3),
pygame.K_x: (2, 4),
pygame.K_c: (2, 5),
pygame.K_v: (3, 4),
pygame.K_b: (3, 5),
pygame.K_n: (4, 5),
}
theta = 0.1 # ugao rotacije
# Pygame setup
pygame.init()
screen = pygame.display.set_mode((1500, 900))
pygame.display.set_caption("6D Hiperkocka – senke na svih 15 2D ravni")
clock = pygame.time.Clock()
font = pygame.font.SysFont(None, 20)
def draw_text(surface, text, pos, color=(255, 255, 255)):
img = font.render(text, True, color)
surface.blit(img, pos)
def main():
global vertices
running = True
while running:
screen.fill((0, 0, 0))
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
keys = pygame.key.get_pressed()
for key in rotation_planes:
if keys[key]:
i, j = rotation_planes[key]
vertices = rotate(vertices, i, j, theta)
# Crtanje svih 15 projekcija
for idx, (i, j) in enumerate(projection_planes):
proj = project_shadow(vertices, light_dir, i, j)
min_p, max_p = proj.min(axis=0), proj.max(axis=0)
scale = 200
margin_x, margin_y = 250 * (idx % 5), 250 * (idx // 5)
offset = np.array([100 + margin_x, 100 + margin_y])
norm_proj = (proj - min_p) / (max_p - min_p + 1e-5) * scale + offset
# Crtanje ivica
for e0, e1 in edges:
p1 = norm_proj[e0]
p2 = norm_proj[e1]
pygame.draw.line(screen, (100, 200, 255), p1, p2, 1)
draw_text(screen, f"dim {i}-{j}", (offset[0] - 30, offset[1] - 50))
draw_text(screen, "Rotacija: q,w,e,r,t,a,s,d,f,z,x,c,v,b,n", (20, 850))
pygame.display.flip()
clock.tick(30)
pygame.quit()
sys.exit()
main()