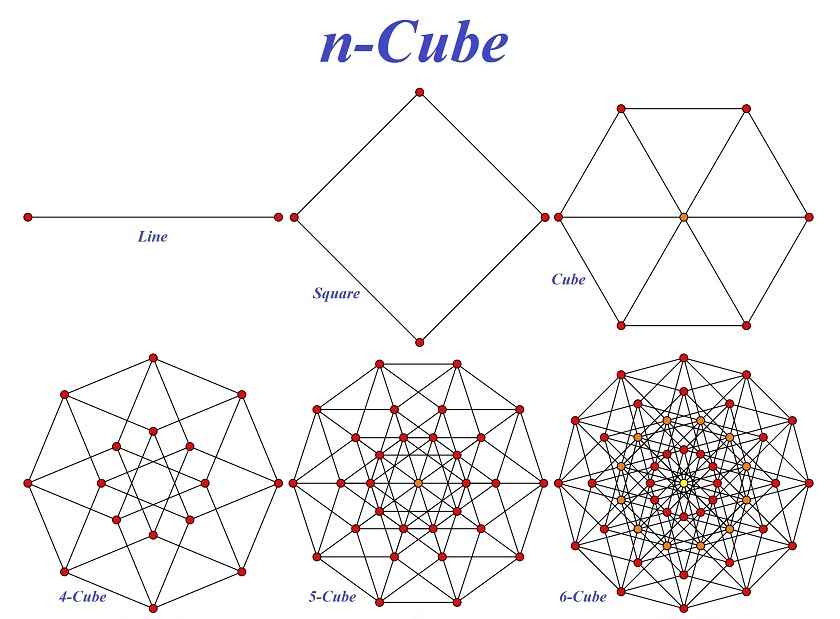
U suštini 4D prostor nije mnogo teži za izračunavanje ili razumevanje u poređenju sa 3D prostorom, ali postoji nekoliko ključnih razlika u načinu kako pristupamo tim prostorima.
Razlike u razumevanju i računanju:
- Matematička sličnost:
- I 3D i 4D prostori koriste vektore i matrice. Na primer, u 3D prostoru, tačka se predstavlja vektorom sa tri koordinate [x,y,z][x, y, z][x,y,z]. U 4D prostoru, ta tačka bi imala četiri koordinate [x,y,z,w][x, y, z, w][x,y,z,w].
- U oba slučaja, računanje operacija kao što su rotacija, transformacije, ili projekcije koristi veoma slične tehnike (npr. matrice za rotaciju ili translaciju).
- Vizualizacija:
- 3D prostor je lakše da vizualizujemo, jer naš svet je trodimenzionalan. Možemo direktno da se “stavimo” u 3D prostor i da ga sagledamo sa različitih perspektiva.
- 4D prostor nije moguće direktno vizualizovati jer naš svet nije četvorodimenzionalan. Moramo da koristimo projekcije 4D objekata u 3D prostor, što nam omogućava da vidimo samo delimične informacije o tom objektu.
- Računanje u 4D:
- Računanje u 4D prostoru uključuje jednu dodatnu koordinatu. Dakle, operacije kao što su rotacije, projekcije, ili pomeranja su slične kao u 3D prostoru, ali se računaju u jednom dodatnom smeru.
- Na primer, ako želimo da rotiramo objekat u 4D prostoru, koristimo 4×4 matrice (umesto 3×3 kao u 3D prostoru).
- Korišćenje u praksi:
- 4D prostori se obično koriste u apstraktnim matematičkim modelima, poput teorije relativnosti ili u kompjuterskoj grafici za generisanje 4D objekata (kao što su tesserakti ili druge hiperkvadrate) koji se potom projektuju u niže dimenzije (najčešće u 3D za vizualizaciju).
- U praktičnom računanju, rad sa 4D prostorima je više matematički, jer ne postoji jednostavan fizički ekvivalent 4D prostora kao što postoji za 3D.
Zašto je lakše računati u 4D nego što je možda ljudima jasno?
- Računanje u višim dimenzijama je jednostavno proširenje već poznatih tehnika iz nižih dimenzija. Dok je teško da “vidimo” 4D, rad sa vektorskim operacijama, matricama rotacija ili projekcijama ostaje isti proces. Na primer:
- Rotacija u 3D prostoru koristi 3×3 matricu i rotira objekat oko osovine. U 4D prostoru koristimo 4×4 matricu, koja omogućava rotaciju u većem broju pravaca (četiri dimenzije umesto tri).
- Projekcija iz 4D u 3D je jednostavno jedna vrsta matematičkog transformisanja koja smanjuje broj dimenzija, slično kao što projekcija 3D objekta na 2D ekranu smanjuje broj dimenzija.
Iako je vizualizacija 4D prostora teža, računanje u 4D prostoru nije znatno složenije od računanja u 3D, jer su svi osnovni principi isti. Sam proces rotacije, translacije ili skaliranja može da se proširi na četvrtu dimenziju dodavanjem samo još jedne koordinate i radom sa 4D vektorima i matricama.
Instalacija potrebnih biblioteka:
pip install pygame PyOpenGL PyOpenGL_accelerate
Programski kod teserakt.py
#teserakt.py
# Instalacija potrebnih zavisnosti:pip install pygame PyOpenGL PyOpenGL_accelerate
import pygame
from pygame.locals import *
from OpenGL.GL import *
from OpenGL.GLU import *
import numpy as np
import sys
# Definicija tesserakt tačaka u 4D
points_4d = [np.array([x, y, z, w]) for x in (-1, 1) for y in (-1, 1)
for z in (-1, 1) for w in (-1, 1)]
# Generisanje ivica (povezane tačke se razlikuju za tačno 2 po jednoj koordinati)
edges = [(i, j) for i in range(len(points_4d)) for j in range(i+1, len(points_4d))
if np.sum(np.abs(points_4d[i] - points_4d[j])) == 2]
# Funkcija za rotaciju u 4D po zadatim osama
def rotate4d(p, angle, axis1, axis2):
sin_a, cos_a = np.sin(angle), np.cos(angle)
rot = np.identity(4)
a, b = {'x': 0, 'y': 1, 'z': 2, 'w': 3}[axis1], {'x': 0, 'y': 1, 'z': 2, 'w': 3}[axis2]
rot[a, a] = cos_a
rot[a, b] = -sin_a
rot[b, a] = sin_a
rot[b, b] = cos_a
return rot @ p
# 4D → 3D perspektivna projekcija
def project_to_3d(p, distance=3.5):
w = 1 / (distance - p[3])
proj_matrix = np.array([
[w, 0, 0, 0],
[0, w, 0, 0],
[0, 0, w, 0]
])
return proj_matrix @ p
# OpenGL inicijalizacija
def init_opengl():
glEnable(GL_DEPTH_TEST)
glMatrixMode(GL_PROJECTION)
gluPerspective(45, 1.0, 0.1, 50.0)
glMatrixMode(GL_MODELVIEW)
def main():
pygame.init()
screen = pygame.display.set_mode((800, 800), DOUBLEBUF | OPENGL)
pygame.display.set_caption("Tesserakt u OpenGL-u")
init_opengl()
# Kamera pozicija
glTranslatef(0.0, 0.0, -10)
# Ugao rotacije
rot_xy = rot_zw = 0.0
rotate_x = rotate_y = 0.0
running = True
while running:
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
# Tasteri za 3D rotaciju
keys = pygame.key.get_pressed()
if keys[K_LEFT]: rotate_y -= 1
if keys[K_RIGHT]: rotate_y += 1
if keys[K_UP]: rotate_x -= 1
if keys[K_DOWN]: rotate_x += 1
rot_xy += 0.01
rot_zw += 0.012
# Primenjuj rotaciju na 4D tačke
rotated = []
for p in points_4d:
p1 = rotate4d(p, rot_xy, 'x', 'y')
p2 = rotate4d(p1, rot_zw, 'z', 'w')
rotated.append(project_to_3d(p2))
# Rotacija scene u 3D
glPushMatrix()
glRotatef(rotate_x, 1, 0, 0)
glRotatef(rotate_y, 0, 1, 0)
# Crtanje ivica
glBegin(GL_LINES)
for i, j in edges:
glColor3fv((0.2, 0.7, 1.0))
glVertex3fv(rotated[i])
glVertex3fv(rotated[j])
glEnd()
glPopMatrix()
pygame.display.flip()
pygame.time.wait(10)
for event in pygame.event.get():
if event.type == QUIT:
running = False
pygame.quit()
sys.exit()
if __name__ == "__main__":
main()
🔍 Kontrole
- Strelice: rotacija 3D prikaza levo/desno, gore/dole
Escili zatvaranje prozora: izlaz