Tesserakt: Prozor u Četvrtu Dimenziju

U svetu u kojem živimo, svakodnevno doživljavamo tri prostorne dimenzije: dužinu, širinu i visinu. Međutim, matematika i teorijska fizika dopuštaju da razmišljamo i o višim dimenzijama, čak i ako ih ne možemo direktno percipirati. Jedan od najupečatljivijih koncepata iz tog višedimenzionalnog sveta jeste tesserakt – četvorodimenziona analogija kocke.

Šta je tesserakt?

Tesserakt je četvorodimenzionalna hiperkocka, baš kao što je kocka trodimenzionalna verzija kvadrata. On ima:

• 16 temena
• 32 ivice
• 24 stranice (2D kvadrati)
• 8 ćelija (3D kocke)

Ako je kvadrat ograničen linijama, a kocka kvadratima, onda je tesserakt ograničen kockama – i to njih osam.

Kako zamišljamo nešto izvan naše dimenzije?

Iako ne možemo direktno videti četvrtu prostornu dimenziju, možemo koristiti matematičke projekcije da je predstavimo u trodimenzionalnom (3D) i dvodimenzionalnom (2D) prostoru – slično kao što senka trodimenzionalnog objekta staje na papir.

Najčešći načini predstavljanja tesserakta uključuju:

• 3D perspektivnu projekciju – prikaz tesserakta kao složene strukture u 3D prostoru, često kao “kocka unutar kocke” povezana ivicama.
• Ortogonalnu projekciju – gde su dimenzije prikazane bez perspektivne distorzije.
• Rotacije kroz 4D prostor – animacije koje prikazuju kako se tesserakt ponaša prilikom rotacije u četvrtoj dimenziji (tzv. 4D spin).

Šta radi ovaj program?

Program koji sledi omogućava korisniku da istraži tesserakt kroz vizuelne projekcije:

• Prikazuje 3D projekciju tesserakta koju možete rotirati i gledati iz različitih uglova.
• Prikazuje tri različite 2D projekcije – svaka otkriva različite aspekte njegove strukture.
• Omogućava animiranu rotaciju u 4D, čime dobijamo uvid u ponašanje tesserakta prilikom promene njegovog stanja u višoj dimenziji.

Ovaj alat je osmišljen kao most između apstraktne matematike i vizuelne intuicije, nudeći priliku da se sagleda lepota i čudnovatost višedimenzionalnih objekata. Bilo da ste matematičar, programer, umetnik ili radoznali um, tesserakt vas poziva da pogledate iza granica trodimenzionalnog sveta.

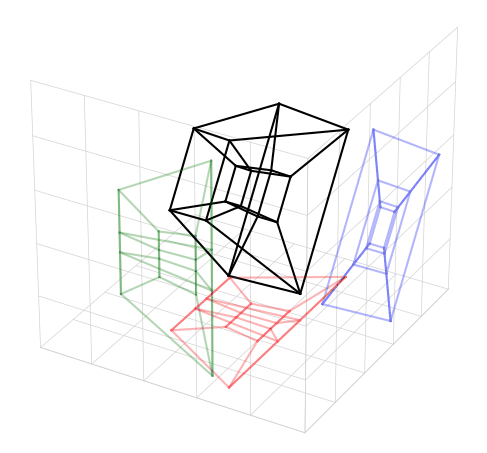
Ovaj program vizualizuje teserakt (4D hiperkocku) u trodimenzionalnom prostoru pomoću projekcije i animacije. Evo detaljnog opisa šta sve radi:

🔢 1. Definisanje temena teserakta (4D hiperkocke)

Teserakt ima 16 temena u 4D prostoru, gde svaka koordinata (x, y, z, w) može biti -1 ili 1. Program kreira listu svih kombinacija tih vrednosti.

vertices = np.array([[x, y, z, w] for x in (-1,1) for y in (-1,1)
                     for z in (-1,1) for w in (-1,1)])

🔗 2. Definisanje ivica teserakta

Dve temene su povezane ivicom ako se razlikuju samo u jednoj koordinati — to znači da su neposredni susedi u hiperkocki.

for i in range(len(vertices)):
    for j in range(i+1, len(vertices)):
        if np.sum(np.abs(vertices[i] - vertices[j])) == 2:
            edges.append((i, j))

🔄 3. Rotacija u 4D prostoru

Program koristi funkciju rotate_4d() da rotira temena teserakta u 4D prostoru (npr. u ravnima XW i YZ) — što stvara efekat “okretanja” teserakta kroz 4. dimenziju.

🎥 4. Perspektivna projekcija iz 4D u 3D

Projekcija se vrši tako da se dimenzija w koristi za dobijanje perspektive — što objekat udaljeniji u w, to izgleda manji u 3D prostoru:

factor = 1 / (2 - w)
projected = points4d[:, :3] * factor[:, np.newaxis]

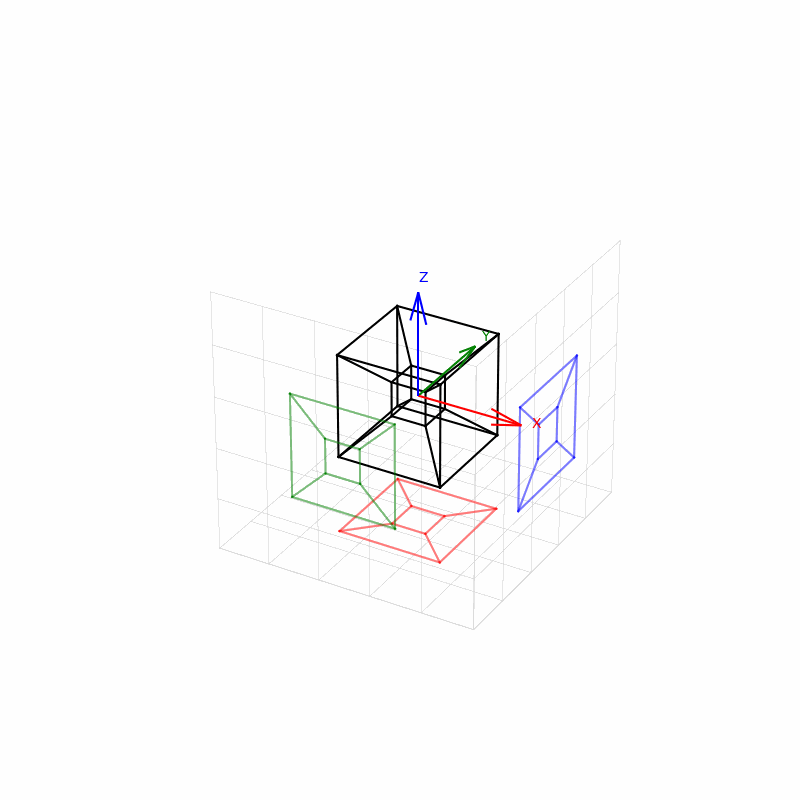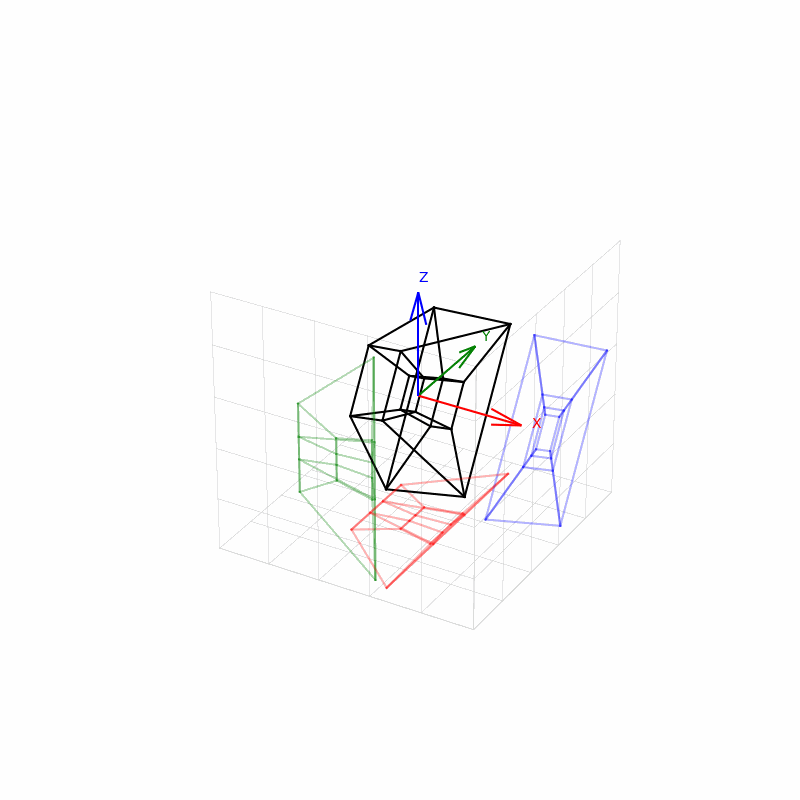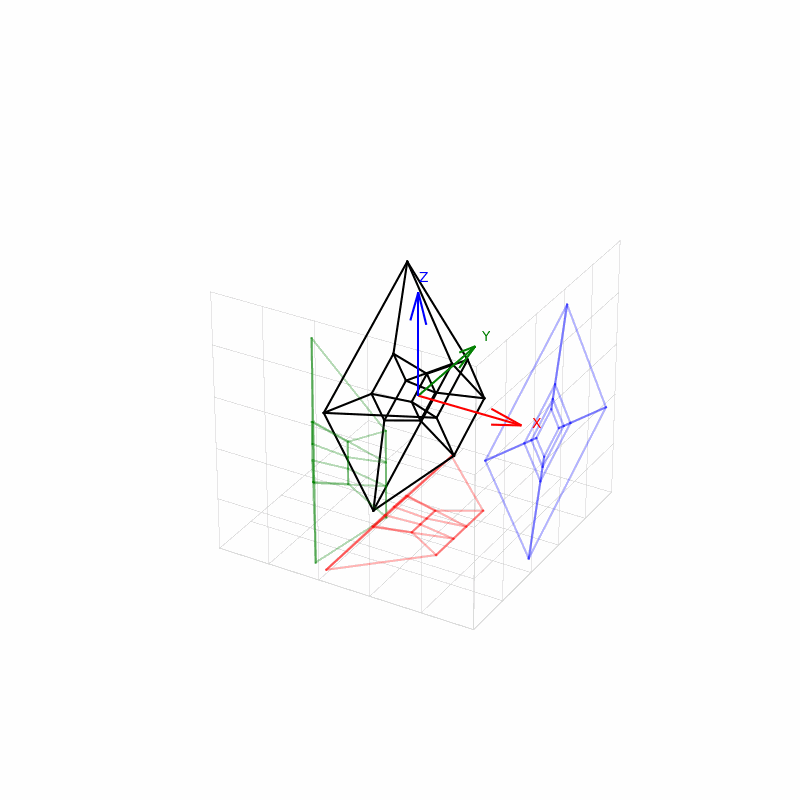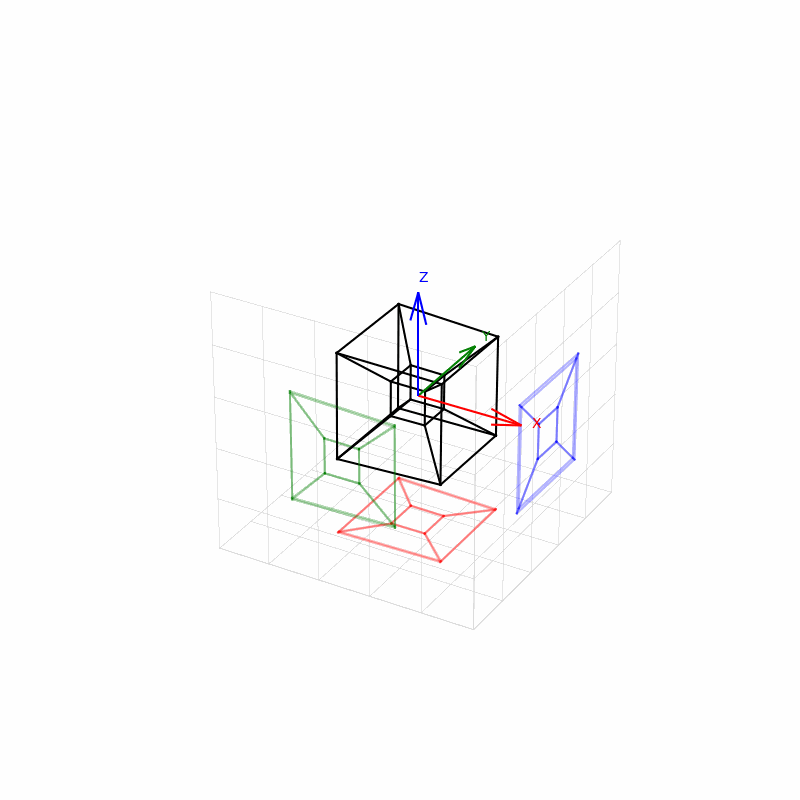
🧱 5. Crtanje glavnog modela i senki

Za svaku ivicu, crtaju se:

• Glavne ivice teserakta (u crnoj boji).
• Senke na XY ravni (Z = -2.5, crvene linije).
• Senke na XZ ravni (Y = -2.5, zelene linije).
• Senke na YZ ravni (X = 2.5, plave linije).

Senke se projektuju tako što se jedna koordinata drži konstantnom (npr. Z = -2.5 za XY ravan), a ostale se koriste iz projektovanih tačaka.

🌀 6. Animacija

FuncAnimation koristi funkciju update() da rotira teserakt i ažurira pozicije njegovih temena i ivica za svaki frejm. Rotacija se menja s vremenom, pa dobijamo utisak da se 4D objekat okreće i baca senke koje se kreću.

💾 7. Snima se GIF

Animacija se snima kao GIF:

ani.save("tesseract_with_grid_and_shadows.gif", writer=PillowWriter(fps=20))

📐 Vizuelni rezultat

• Vidimo projekciju teserakta u 3D prostoru.
• Senke daju dodatni prostorono-orijentacioni kontekst.
• Rotacija kroz 4D omogućava bolje razumevanje strukture hiperkocke.

Instalacija svih potrebnih paketa:

pip install numpy matplotlib pillow ipywidgets

Programski kod teserakt.py

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.lines import Line2D
from matplotlib.animation import FuncAnimation, PillowWriter

# Teserakt u 4D
vertices = np.array([[x, y, z, w] for x in (-1,1) for y in (-1,1)
                     for z in (-1,1) for w in (-1,1)])

edges = []
for i in range(len(vertices)):
    for j in range(i+1, len(vertices)):
        if np.sum(np.abs(vertices[i] - vertices[j])) == 2:
            edges.append((i, j))

def rotate_4d(v, angle, i, j):
    c, s = np.cos(angle), np.sin(angle)
    R = np.identity(4)
    R[[i,i,j,j],[i,j,i,j]] = c, -s, s, c
    return v @ R.T

def project_to_3d(points4d):
    w = points4d[:, 3]
    factor = 1 / (2 - w)
    return points4d[:, :3] * factor[:, np.newaxis]

fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')
ax.set_xlim([-3, 3])
ax.set_ylim([-3, 3])
ax.set_zlim([-3, 3])
ax.set_box_aspect([1, 1, 1])
ax.axis('off')

# Oznake osa
ax.quiver(0, 0, 0, 2, 0, 0, color='r')
ax.quiver(0, 0, 0, 0, 2, 0, color='g')
ax.quiver(0, 0, 0, 0, 0, 2, color='b')
ax.text(2.2, 0, 0, 'X', color='r')
ax.text(0, 2.2, 0, 'Y', color='g')
ax.text(0, 0, 2.2, 'Z', color='b')

# Mreže (statične ravni)
def draw_plane_grid():
    grid_range = np.linspace(-2.5, 2.5, 6)

    for x in grid_range:
        ax.plot([x, x], [grid_range[0], grid_range[-1]], [-2.5, -2.5], color='lightgray', lw=0.5)  # XY
        ax.plot([x, x], [-2.5, -2.5], [grid_range[0], grid_range[-1]], color='lightgray', lw=0.5)  # XZ

    for y in grid_range:
        ax.plot([grid_range[0], grid_range[-1]], [y, y], [-2.5, -2.5], color='lightgray', lw=0.5)  # XY
        ax.plot([2.5, 2.5], [y, y], [grid_range[0], grid_range[-1]], color='lightgray', lw=0.5)    # YZ

    for z in grid_range:
        ax.plot([2.5, 2.5], [grid_range[0], grid_range[-1]], [z, z], color='lightgray', lw=0.5)    # YZ
        ax.plot([grid_range[0], grid_range[-1]], [-2.5, -2.5], [z, z], color='lightgray', lw=0.5)  # XZ

draw_plane_grid()

# Kreiraj prazne linije za update
lines = []
shadow_xy = []
shadow_xz = []
shadow_yz = []

for edge in edges:
    l, = ax.plot([], [], [], color='black')
    lines.append(l)
    sxy, = ax.plot([], [], [], color='red', alpha=0.3)
    sxz, = ax.plot([], [], [], color='green', alpha=0.3)
    syz, = ax.plot([], [], [], color='blue', alpha=0.3)
    shadow_xy.append(sxy)
    shadow_xz.append(sxz)
    shadow_yz.append(syz)

def update(frame):
    angle = frame * np.pi / 100
    rotated = rotate_4d(vertices, angle, 0, 3)
    rotated = rotate_4d(rotated, angle / 2, 1, 2)
    projected = project_to_3d(rotated)

    for idx, (i, j) in enumerate(edges):
        p1, p2 = projected[i], projected[j]

        # Glavna ivica
        lines[idx].set_data([p1[0], p2[0]], [p1[1], p2[1]])
        lines[idx].set_3d_properties([p1[2], p2[2]])

        # Senke
        shadow_xy[idx].set_data([p1[0], p2[0]], [p1[1], p2[1]])
        shadow_xy[idx].set_3d_properties([-2.5, -2.5])

        shadow_xz[idx].set_data([p1[0], p2[0]], [-2.5, -2.5])
        shadow_xz[idx].set_3d_properties([p1[2], p2[2]])

        shadow_yz[idx].set_data([2.5, 2.5], [p1[1], p2[1]])
        shadow_yz[idx].set_3d_properties([p1[2], p2[2]])

    return lines + shadow_xy + shadow_xz + shadow_yz

ani = FuncAnimation(fig, update, frames=200, interval=50, blit=True)

# Sačuvaj kao GIF ako želiš:
ani.save("tesseract_static_planes.gif", writer=PillowWriter(fps=20))

plt.show()