Voronoi kupola je fascinantna struktura koja kombinuje geometriju, prirodne obrasce i estetski izražaj. Voronoi kupola je sferna ili hemisferna konstrukcija čija je površina podeljena prema Voronoi dijagramu — geometrijskoj strukturi koja deli prostor prema najbližim tačkama (semenkama). Na sferi, Voronoi ćelije formiraju mozaik poligona nalik na prirodne oblike, poput ćelija pčelinjeg saća, koralnih struktura, ili pukotina u zemljištu.

• Iako je Voronoi dijagram matematički konstrukt, u prirodi se pojavljuje spontano: u biološkim tkivima, krastama zemlje, rasporedu vena na listu, pa čak i u pukotinama na staklu.
• Kada se primeni na sfernu površinu, generiše organske, nepravilne poligone koji ipak deluju uravnoteženo.
• Umetnici i arhitekte vole ga zbog kombinacije haosa i harmonije.

Tehnički postupak (generisanje):

1. Generiši skup tačaka ravnomerno raspoređenih na sferi (npr. pomoću Fibonacci rasporeda).
2. Izračunaj sferni Voronoi dijagram (koristeći scipy.spatial.SphericalVoronoi ili pyvoro za 3D).
3. Projiciraj ćelije na sferu/kupolu i renderuj kao poligonalne površine.
4. Prikaz i izvoz u STL/PLY za 3D štampu ili vizualizaciju.

Upotreba:

• Arhitektura: kao krovne konstrukcije, svetlarnici, kupole koje stvaraju igru svetlosti i senke.
• Umetnost i dizajn: skulpture, lampe, fasade sa dinamičnim svetlosnim efektima.
• Vizualizacija podataka: kao metafora za raspodelu resursa, biologiju ćelija, socijalne mreže…

Vizuelni primeri i inspiracije:

• Krov Zaha Hadid škole u Pekingu (organska mreža)
• Digitalne skulpture koje imitiraju koralne strukture
• Generativna umetnost bazirana na prirodnim obrascima

Detaljna matematika Voronoi kupole na sferi

Voronoi kupola predstavlja podelu površine sfere na poligonalne oblasti (Voronoi ćelije), gde svaka oblast pripada jednoj zadatoj tački (generativnoj tački) i sadrži sve tačke sfere bliže toj generativnoj tački nego bilo kojoj drugoj.

1. Geometrija sfere

Neka je sfera poluprečnika \( R > 0 \), centrirana u koordinatnom početku. Svaka tačka na sferi zadana je vektorom:

gde je \(\|\mathbf{x}\| = \sqrt{x^2 + y^2 + z^2}\) euklidska norma.

2. Raspored generativnih tačaka

Izbor tačaka \(\{\mathbf{p}_i\}_{i=1}^n\) na sferi treba da zadovolji što ravnomernije pokrivanje sfere. Jedan od često korišćenih pristupa je korišćenje Fibonaccijeve spirale za raspored tačaka, koji daje niz tačaka približno ravnomerno raspoređenih na površini sfere.

Matematički, tačke su određene parametrima:

Ovim se postiže ravnomeran raspored \(n\) tačaka \(\mathbf{p}_i\) po površini sfere.

3. Definicija sfernog Voronoi dijagrama

Neka su \(\{\mathbf{p}_i\}\) generativne tačke na sferi. Sferni Voronoi dijagram deli sferu na oblasti \(V_i\), gde je:

Ovde je \(d_g(\mathbf{x}, \mathbf{y})\) geodetska (veliki krug) udaljenost na sferi između tačaka \(\mathbf{x}\) i \(\mathbf{y}\), definisana kao:

gde je \(\mathbf{x} \cdot \mathbf{y} = x_1 y_1 + x_2 y_2 + x_3 y_3\) skalarni proizvod vektora.

4. Konstrukcija Voronoi ćelija

Voronoi ćelija \(V_i\) je geometrijski presečak hemisfera definisanih preko ravni koje su ortogonalne na pravu koja povezuje \(\mathbf{p}_i\) i \(\mathbf{p}_j\).

Za svaku paru tačaka \(\mathbf{p}_i, \mathbf{p}_j\), definišemo ravninu bisektrisu:

Za sfernu Voronoi ćeliju, uzimamo onu stranu sfere gde je \(\mathbf{x}\) bliže \(\mathbf{p}_i\):

Ukratko, svaka ćelija je konveksni poligon na površini sfere omeđen lukovima velikih krugova.

5. Geometrijski objekat Voronoi kupole

Voronoi kupola se može predstaviti kao geometrijski mesh gde su:

• Vrhovi tačke preseka ivica Voronoi ćelija (vrhovi regija)
• Ivici lukovi velikih krugova (geodetske linije) koje spajaju vrhove
• Lica poligoni sa ivicama na sferi – Voronoi ćelije

Svaka Voronoi ćelija može se dalje podeliti na trouglove povezivanjem centra ćelije sa vrhovima ćelije, što omogućava triangulaciju površine kupole.

6. Matematički izrazi za površinu Voronoi ćelije

Površina Voronoi ćelije na sferi može se aproksimirati sumom površina trouglova sa vrhovima na sferi. Površina trougla na sferi definisana je sfernim višekutom i računa se pomoću Gaussove formule:

gde je \(m\) broj uglova trougla (za trougao \(m=3\)), a \(\theta_k\) su unutrašnji uglovi sfernog trougla definisani velikim krugovima.

7. Zaključak

Matematički opis Voronoi kupole zasnovan je na preciznoj geometriji sfere i dela površine na Voronoi ćelije koje su sferni poligoni omeđeni velikim krugovima. Ove ćelije se izračunavaju kao preseci hemisfera i služe za konstrukciju geometrijske mreže kupole sa specifičnim geometrijskim i strukturnim svojstvima.

Ova struktura se koristi u različitim oblastima, uključujući arhitekturu, 3D modelovanje, geodeziju i kompjutersku grafiku.

Program za izradu Voronoi kupole

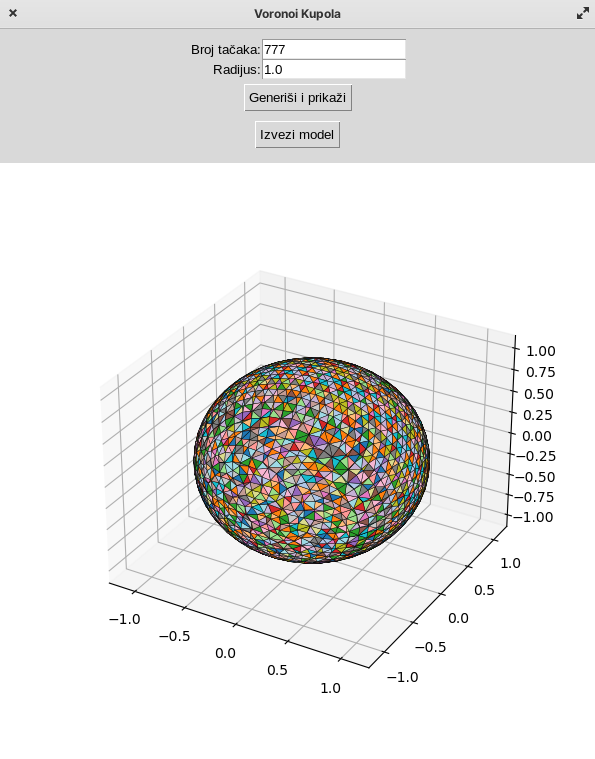
Instalacija svih potrebnih biblioteka da bi program radio:

pip install numpy scipy matplotlib trimesh ezdxf

Programski kod Voronoi.py

import tkinter as tk
from tkinter import ttk, filedialog, messagebox
import numpy as np
from scipy.spatial import SphericalVoronoi
import matplotlib.pyplot as plt
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
from mpl_toolkits.mplot3d.art3d import Poly3DCollection

import trimesh
import ezdxf
import os
from collections import defaultdict

def fibonacci_sphere(samples=100, radius=1.0):
    points = []
    offset = 2.0 / samples
    increment = np.pi * (3.0 - np.sqrt(5.0))
    for i in range(samples):
        y = ((i * offset) - 1) + (offset / 2)
        r = np.sqrt(1 - y * y)
        phi = i * increment
        x = np.cos(phi) * r
        z = np.sin(phi) * r
        points.append([x * radius, y * radius, z * radius])
    return np.array(points)

def generate_voronoi_dome(num_points=100, radius=1.0):
    points = fibonacci_sphere(num_points, radius)
    sv = SphericalVoronoi(points, radius)
    sv.sort_vertices_of_regions()

    vertices = []
    faces = []
    for region in sv.regions:
        if len(region) >= 3:
            polygon = [sv.vertices[i] for i in region]
            center = np.mean(polygon, axis=0)
            center_index = len(vertices)
            vertices.append(center)
            for i in range(len(polygon)):
                a = polygon[i]
                b = polygon[(i + 1) % len(polygon)]
                a_index = len(vertices)
                b_index = len(vertices) + 1
                vertices.extend([a, b])
                tri = np.array([center, a, b])
                normal = np.cross(tri[1] - tri[0], tri[2] - tri[0])
                if np.dot(normal, center) < 0:
                    faces.append([center_index, b_index, a_index])
                else:
                    faces.append([center_index, a_index, b_index])
    return np.array(vertices), np.array(faces)

def export_mesh_to_dxf(mesh, filename):
    doc = ezdxf.new(dxfversion='R2010')
    msp = doc.modelspace()

    edges = mesh.edges_unique
    vertices = mesh.vertices

    for edge in edges:
        start = vertices[edge[0]]
        end = vertices[edge[1]]
        msp.add_line(start.tolist(), end.tolist())

    doc.saveas(filename)
    print(f"DXF izvezen u: {filename}")

def compute_triangle_areas(vertices, faces):
    # Vrati listu površina za svaki trougao
    v0 = vertices[faces[:, 0]]
    v1 = vertices[faces[:, 1]]
    v2 = vertices[faces[:, 2]]
    areas = 0.5 * np.linalg.norm(np.cross(v1 - v0, v2 - v0), axis=1)
    return areas

def assign_colors_by_area(areas, tolerance=1e-5):
    # Grupisanje trouglova sa slicnim povrsinama u iste boje
    unique_areas = []
    color_indices = np.full(len(areas), -1, dtype=int)

    for i, area in enumerate(areas):
        assigned = False
        for j, ua in enumerate(unique_areas):
            if abs(area - ua) < tolerance:
                color_indices[i] = j
                assigned = True
                break
        if not assigned:
            unique_areas.append(area)
            color_indices[i] = len(unique_areas) - 1

    # Generisi boje u RGB, po broju grupa
    num_groups = len(unique_areas)
    cmap = plt.get_cmap("tab20")  # Do 20 različitih boja, možeš promeniti
    colors = np.array([cmap(i % 20)[:3] for i in color_indices])  # RGB, bez alfa

    # Scale u 0-255 za PLY
    colors_255 = (colors * 255).astype(np.uint8)
    return colors_255

class VoronoiDomeApp:
    def __init__(self, root):
        self.root = root
        root.title("Voronoi Kupola")

        self.frame = ttk.Frame(root)
        self.frame.pack(padx=10, pady=10)

        ttk.Label(self.frame, text="Broj tačaka:").grid(row=0, column=0, sticky='e')
        self.points_entry = ttk.Entry(self.frame)
        self.points_entry.insert(0, "200")
        self.points_entry.grid(row=0, column=1)

        ttk.Label(self.frame, text="Radijus:").grid(row=1, column=0, sticky='e')
        self.radius_entry = ttk.Entry(self.frame)
        self.radius_entry.insert(0, "1.0")
        self.radius_entry.grid(row=1, column=1)

        self.gen_button = ttk.Button(self.frame, text="Generiši i prikaži", command=self.generate)
        self.gen_button.grid(row=2, column=0, columnspan=2, pady=5)

        self.export_button = ttk.Button(self.frame, text="Izvezi model", command=self.export_all_formats)
        self.export_button.grid(row=3, column=0, columnspan=2, pady=5)

        self.figure = plt.Figure(figsize=(6, 6))
        self.ax = self.figure.add_subplot(111, projection='3d')
        self.canvas = FigureCanvasTkAgg(self.figure, master=root)
        self.canvas.get_tk_widget().pack()

        self.vertices = None
        self.faces = None
        self.face_colors = None

    def generate(self):
        try:
            num_points = int(self.points_entry.get())
            radius = float(self.radius_entry.get())
            self.vertices, self.faces = generate_voronoi_dome(num_points, radius)

            # Izračunaj površine trouglova i dodeli boje
            areas = compute_triangle_areas(self.vertices, self.faces)
            self.face_colors = assign_colors_by_area(areas)

            self.draw()
        except Exception as e:
            messagebox.showerror("Greška", str(e))

    def draw(self):
        self.ax.clear()
        collection = Poly3DCollection(self.vertices[self.faces], facecolors=self.face_colors / 255, edgecolor='k', linewidth=0.3)
        self.ax.add_collection3d(collection)
        scale = np.max(np.abs(self.vertices)) * 1.1
        self.ax.auto_scale_xyz([-scale, scale], [-scale, scale], [-scale, scale])
        self.canvas.draw()

    def export_all_formats(self):
        if self.vertices is None or self.faces is None:
            messagebox.showwarning("Upozorenje", "Prvo generiši model.")
            return

        base_path = filedialog.asksaveasfilename(defaultextension=".stl",
                                                 filetypes=[("STL", "*.stl"),
                                                            ("PLY", "*.ply"),
                                                            ("DXF", "*.dxf")])
        if not base_path:
            return

        base_name, _ = os.path.splitext(base_path)

        try:
            stl_path = base_name + ".stl"
            ply_path = base_name + ".ply"
            dxf_path = base_name + ".dxf"

            # Kreiraj trimesh objekat i dodeli boje licima za PLY
            mesh = trimesh.Trimesh(vertices=self.vertices, faces=self.faces, process=False)
            mesh.visual.face_colors = np.hstack((self.face_colors, np.full((len(self.face_colors),1),255, dtype=np.uint8)))

            mesh.rezero()
            mesh.update_faces(mesh.unique_faces())
            mesh.update_faces(mesh.nondegenerate_faces())
            mesh.remove_infinite_values()
            mesh.fix_normals()

            print(f"[INFO] Eksportujem STL u: {stl_path}")
            mesh.export(stl_path, file_type='stl')

            print(f"[INFO] Eksportujem PLY u: {ply_path}")
            mesh.export(ply_path, file_type='ply')

            print(f"[INFO] Eksportujem DXF u: {dxf_path}")
            export_mesh_to_dxf(mesh, dxf_path)

            messagebox.showinfo("Uspeh", f"Model je sačuvan u:\n{stl_path}\n{ply_path}\n{dxf_path}")
        except Exception as e:
            messagebox.showerror("Greška", str(e))


if __name__ == '__main__':
    root = tk.Tk()
    app = VoronoiDomeApp(root)
    root.mainloop()

Izlazni fajlovi:

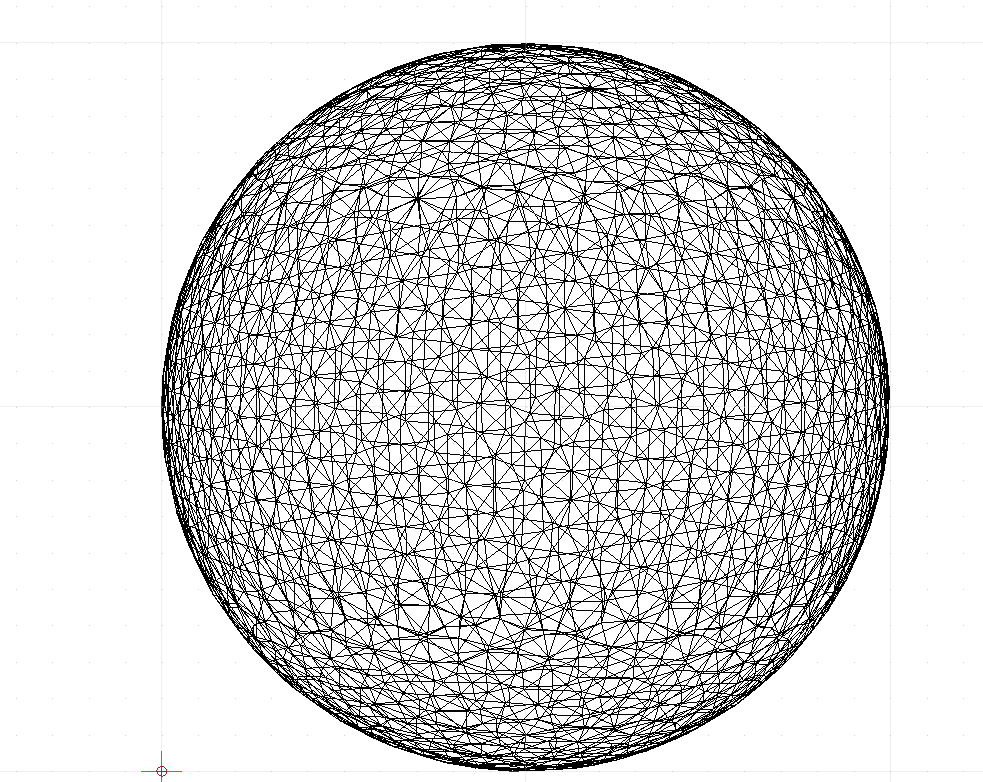
Relevantni radovi o Voronoi kupoli:

1. Circle packing on spherical caps

• Autori: N. S. D. D. P. et al.
• Link: https://arxiv.org/abs/2406.02851v1
• Sažetak: Ovaj rad istražuje problem gustoće pakovanja istih krugova (diskova) na sfernim kapama, što je povezano sa geometrijom i rasporedom Voronoi ćelija na sferi.

2. Tessellations and Pattern Formation in Plant Growth and Development

• Autori: R. M. et al.
• Link: https://arxiv.org/abs/1209.2937
• Sažetak: Rad analizira nastanak poligonalnih obrazaca u tkivima biljaka, koji su slični Voronoi teselacijama, što može biti korisno kao biološki model za arhitektonske strukture.

3. Voronoi Diagram Generation Process

• Autori: F. B. et al.
• Link: https://arxiv.org/pdf/0804.0279.pdf
• Sažetak: Detaljan prikaz metoda za generisanje Voronoi dijagrama u različitim geometrijskim kontekstima, uključujući sferne površine.

4. Shape Morphing Metamaterials

• Autori: M. M. et al.
• Link: https://arxiv.org/abs/2501.14804v1
• Sažetak: Rad o metamaterijalima sa prilagodljivim oblicima koji se baziraju na geometrijskim principima, što može biti korisno za projektovanje dinamičkih Voronoi kupola.

Preporučene ključne reči za pretragu na arXiv.org

“Voronoi tessellation architecture”

“Voronoi dome”

“Spherical Voronoi diagram”

“Geodesic dome Voronoi”