Octahedral 5V Geodetska kupola – „Mexican Method”

Uvod

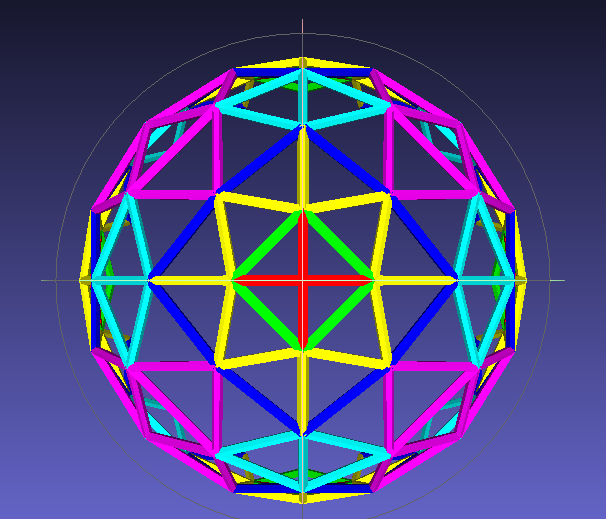
Geodetske kupole predstavljaju izuzetno efikasan način pokrivanja prostora koristeći minimalan materijal uz maksimalnu strukturnu stabilnost. One se baziraju na geometrijskoj transformaciji osnovnih poliedara – najčešće ikosaedra i oktaedra – kroz pravilnu deobu njihovih trougaonih površina. Među različitim metodama deobe trouglova, tzv. „Mexican Method”, razvijen od strane meksičkog matematičara Hectora Alfreda Hernándeza Hernándeza, zauzima posebno mesto zbog svoje optimizacije dužina šipki.

Osnovna ideja “Mexican Method”

Za razliku od konvencionalne „klasične“ deobe (Frequency method) gde se svaka stranica trougla deli linearno, Mexican Method koristi podelu po linijama konstantne širine unutar trougla, pri čemu šipke slede specifične paralelne pravce. Svaka šipka pripada jednoj od tri dominantne orijentacije, i sve šipke istog pravca imaju identične dužine.

➡️ Broj unikatnih dužina šipki u ovoj metodi je uvek jednak frekvenciji (V), što značajno pojednostavljuje proizvodnju i montažu.

Primena na oktaedarsku geometriju

Kada se metoda primeni na oktaedarsku osnovu:

• Osnovni poliedar (oktaedar) ima 8 trouglastih lica.
• Svako lice se deli na V × V manjih trouglova (npr. 5V → 25 pod-trouglova po licu).
• Primenjuje se Mexican Method podela, pri čemu se linije šipki kreću duž tri paralelna pravca, što formira tri porodice šipki.

Međutim, zbog pravilne kombinacije ovih pravaca, stvara se mreža u kojoj se sve šipke mogu svrstati u tačno V različitih dužina – označenih slovima A, B, C, D, E za 5V.

Matematička osnova

1. Deoba trougla Mexican metodom

Zamislimo trougao sa temenima A,B,CA, B, CA,B,C. Njegova podela vrši se u tri pravca koji odgovaraju stranama:

• od A ka B: horizontalna mreža,
• od B ka C: leva dijagonala,
• od C ka A: desna dijagonala.

Za frekvenciju V, trougao se deli tako da:

• Ukupno imamo V²manjih trouglova (dela),
• Svaka nova tačka se može dobiti kao linearna kombinacija:

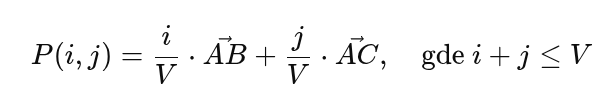
Nakon generisanja tačaka, svi vektori šipki koji povezuju susedne tačke biće klasifikovani prema pravcu (jedan od tri). Pošto je distanca između takvih tačaka konstantna u svakom pravcu, dužine se ponavljaju.

2. Normalizacija na sferu

Da bi se od ravne mreže formirala kupola, sve tačke se projektuju na sferu: P′=R⋅P∥P∥P’ = R \cdot \frac{P}{\|P\|}P′=R⋅∥P∥P​

gde je RRR željeni poluprečnik kupole.

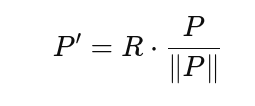
3. Ograničenje na hemisferu

Za arhitektonsku primenu koristi se samo gornja hemisfera, tj. sve tačke sa z ≥ 0. Ovo se obično postiže rotacijom cele sfere tako da „donji obod“ bude ravan, a rezultantna kupola funkcionalna za postavljanje na temelj.

Prednosti Mexican metoda

✅ Ravnomerna raspodela opterećenja: Šipke istih dužina i orijentacije omogućavaju lakšu analizu napona i sila.

✅ Proizvodna efikasnost: Manje tipova šipki → jeftinija proizvodnja.

✅ Estetska simetrija: Mreža podseća na pravilne tekstilne strukture, pogodna za arhitekturu i umetnost.

Ograničenja

🔸 Tačnost metode opada za V > 5 – zbog geometrijskih deformacija pri projektovanju na sferu, jednakost dužina se gubi.

🔸 Teže modelovanje manuelno – potrebni su programski alati za generisanje (kao npr. program koji smo napisali u Pythonu).

Zaključak

Mexican Method predstavlja inovativan i praktičan pristup konstrukciji geodetskih kupola, posebno kada se koristi sa oktaedarskom geometrijom. Njegova efikasnost u pojednostavljivanju broja elemenata i ujednačavanju dužina šipki čini ga idealnim za inženjersku i arhitektonsku primenu u malim i srednje velikim kupolama (do frekvencije 5).

U kombinaciji sa softverskim alatima, ovaj metod pruža moćnu osnovu za pravljenje modularnih, održivih i estetski privlačnih konstrukcija.

✅ Potrebne biblioteke

✅ Instalacija potrebnih eksternih paketa

U terminalu (ili CMD ako koristiš Windows), pokreni sledeću komandu:

pip install numpy trimesh ezdxf scikit-learn

ili:

pip3 install numpy trimesh ezdxf scikit-learn

Programski kod za mex.py

import numpy as np
import trimesh
import colorsys
import itertools
from collections import defaultdict
import os
import ezdxf

def generate_octahedron_faces():
    vertices = np.array([
        [1, 0, 0], [-1, 0, 0],
        [0, 1, 0], [0, -1, 0],
        [0, 0, 1], [0, 0, -1]
    ])
    faces = np.array([
        [0, 2, 4], [2, 1, 4],
        [1, 3, 4], [3, 0, 4],
        [0, 5, 2], [2, 5, 1],
        [1, 5, 3], [3, 5, 0]
    ])
    return vertices, faces

def subdivide_triangle(v1, v2, v3, frequency):
    def normalize(v): return v / np.linalg.norm(v)
    vertices = {}
    faces = []
    for i in range(frequency + 1):
        for j in range(frequency + 1 - i):
            t1 = i / frequency
            t2 = j / frequency
            t3 = 1.0 - t1 - t2
            point = t1 * v1 + t2 * v2 + t3 * v3
            vertices[(i, j)] = normalize(point)
    for i in range(frequency):
        for j in range(frequency - i):
            vtx1 = vertices[(i, j)]
            vtx2 = vertices[(i + 1, j)]
            vtx3 = vertices[(i, j + 1)]
            faces.append([vtx1, vtx2, vtx3])
            if j + i < frequency - 1:
                vtx4 = vertices[(i + 1, j + 1)]
                faces.append([vtx2, vtx4, vtx3])
    return faces

def auto_epsilon(frequency):
    return {
        1: 1e-5,
        2: 1e-4,
        3: 1e-3,
        4: 0.05,
        5: 0.025  # suženo za veću preciznost
    }.get(frequency, 0.05)

def cluster_lengths(lengths, epsilon, target_clusters):
    from sklearn.cluster import KMeans
    data = np.array(lengths).reshape(-1, 1)
    kmeans = KMeans(n_clusters=target_clusters, n_init='auto', random_state=0).fit(data)
    labels = kmeans.labels_
    clusters = [[] for _ in range(target_clusters)]
    for idx, label in enumerate(labels):
        clusters[label].append(lengths[idx])
    cluster_representatives = [np.mean(c) for c in clusters]
    return cluster_representatives, clusters

def generate_dome(frequency, radius):
    base_vertices, base_faces = generate_octahedron_faces()
    all_edges = set()
    for face in base_faces:
        v1, v2, v3 = [base_vertices[i] for i in face]
        tris = subdivide_triangle(v1, v2, v3, frequency)
        for tri in tris:
            for i, j in itertools.combinations([0, 1, 2], 2):
                a, b = tri[i], tri[j]
                if a[2] >= 0 or b[2] >= 0:
                    edge = tuple(sorted([tuple(a), tuple(b)]))
                    all_edges.add(edge)

    all_edges = list(all_edges)
    edge_lengths = [np.linalg.norm(np.array(a) - np.array(b)) for a, b in all_edges]
    cluster_centers, clusters = cluster_lengths(edge_lengths, auto_epsilon(frequency), frequency)

    strut_map = {}
    struts_by_type = defaultdict(list)
    tubes = []
    colors = [colorsys.hsv_to_rgb(i / len(cluster_centers), 1.0, 1.0) for i in range(len(cluster_centers))]
    color_map = {center: color for center, color in zip(cluster_centers, colors)}

    for (a, b), l in zip(all_edges, edge_lengths):
        for i, center in enumerate(cluster_centers):
            if abs(l - center) <= auto_epsilon(frequency):
                typ = chr(65 + i)
                strut_map[center] = typ
                color = color_map[center]
                a3 = np.array(a) * radius
                b3 = np.array(b) * radius
                struts_by_type[typ].append((a3, b3))
                tube = trimesh.creation.cylinder(radius=0.02 * radius, segment=[a3, b3], sections=6)
                tube.visual.vertex_colors = [np.array(color) * 255] * len(tube.vertices)
                tubes.append(tube)
                break

    return tubes, struts_by_type, strut_map, color_map, cluster_centers, clusters, edge_lengths

def export_results(radius, frequency, tubes, struts_by_type, strut_map, color_map, cluster_centers, clusters, edge_lengths):
    base_name = f"dome_R{radius}_V{frequency}"
    os.makedirs("output", exist_ok=True)
    mesh = trimesh.util.concatenate(tubes)
    mesh.export(f"output/{base_name}.ply")
    mesh.export(f"output/{base_name}.stl")
    with open(f"output/{base_name}.txt", "w") as f:
        f.write(f"Geodesic Dome Report (R={radius}, V={frequency})\n\n")
        for i, (center, cluster) in enumerate(zip(cluster_centers, clusters)):
            typ = chr(65 + i)
            color = tuple(round(c * 255) for c in color_map[center])
            count = sum(abs(l - center) <= auto_epsilon(frequency) for l in edge_lengths)
            f.write(f"Type {typ}: Length={round(center * radius, 3)}, Count={count}, Color RGB={color}\n")

def export_dxf(radius, frequency, struts_by_type):
    base_name = f"dome_R{radius}_V{frequency}"
    os.makedirs("output", exist_ok=True)
    doc = ezdxf.new(dxfversion="R2010")
    msp = doc.modelspace()
    for strut_type, struts in struts_by_type.items():
        if not doc.layers.has_entry(strut_type):
            doc.layers.add(name=strut_type)
        for a, b in struts:
            msp.add_line(a, b, dxfattribs={"layer": strut_type})
    doc.saveas(f"output/{base_name}.dxf")

def main():
    print("=== Octahedral Geodesic Dome Generator (Mexican Method) ===")
    radius = float(input("Unesi poluprečnik kupole (npr. 2.0): "))
    frequency = int(input("Unesi frekvenciju (1–5): "))
    print(f"Generišem kupolu za R={radius}, V={frequency}...")
    tubes, struts_by_type, strut_map, color_map, cluster_centers, clusters, edge_lengths = generate_dome(frequency, radius)
    export_results(radius, frequency, tubes, struts_by_type, strut_map, color_map, cluster_centers, clusters, edge_lengths)
    export_dxf(radius, frequency, struts_by_type)
    print("Završeno. Rezultati su u fascikli 'output/'.")

if __name__ == "__main__":
    main()