O dimenziji koja se ne može nacrtati

Hajde da napravimo jedan misaoni eksperiment. Recimo, da postoji dvodimenzioni svet u kojem žive dvodimenziona bića. Oni poseduju samo širinu i dužinu ne poseduju visinu. Kada staviš trodimenzionu kocku u taj svet oni opažaju kvadrat, kada staviš, tetraedar oni opažaju trougao, kada staviš stolicu oni opažaju 4 kvadrata pravilno raspoređena. Nekim načinom uzimam jedno dvodimenziono biće koje je vrhunski matematičar i filosof i koje ima sva moguća znanja o dvodimenzionom svetu. Dodajem mu na neki način treću dimenziju tako da on sada ima mogućnost percepcije trodimenzionog sveta i uvodim ga u trodimenzioni svet. Provodim ga kroz trodimenzioni svet i pokazujem mu sve iz tog sveta. Potom mu oduzimam treću dimenziju (visinu) i vraćam ga u njegov dvodimenzioni svet. Šta bi on mogao da kaže svojim dvodimenzionim matematičarima i filosofima o trodimenzionom svetu koji je obišao i video?

Zanimljiv misaoni eksperiment – nalik čuvenoj priči „Flatland“ Edwina Abbotta, ali s mnogo dubljom filozofskom i epistemološkom ambicijom.

U toj sceni, dvodimenzionalno biće koje si „uzdigao“ u treću dimenziju ne bi se moglo vratiti isto. Ne samo što je iskustveno doživelo novu dimenziju, već se njegov jezik, pojmovi i matematički modeli više ne bi savršeno uklapali u ograničenja dvodimenzionalnog sveta. A evo kako bi mogla izgledati njegova poruka dvodimenzionalnim kolegama:

1. O nemogućnosti izražavanja (jezik i pojam treće dimenzije)
Rekao bi:
„Postoji pravac koji nije ni levo-desno, ni gore-dole, ali je ipak realan. To je pravac koji nikada ne preseče naš svet, ali se iz svakog mesta može poći u tom pravcu. Niko od vas to ne može da zamisli, ali ja sam bio tamo.“

Za ostale, to bi zvučalo kao paradoks: „Ako nije ni X ni Y, onda ne postoji.“

2. O pojavama u tom višem svetu
Pokušao bi da objasni:
„Ono što vi zovete kvadratom, to je samo senka jednog višeg oblika. Telo koje vi vidite kao kvadrat može se transformisati neprekidno u trougao, trapez ili krug – a da ne nestane. Sve je to ista stvar, samo gledano iz više perspektive.“

Ovde bi kolege pitali: „Kako kvadrat može da postane krug bez da se promeni broj tačaka?“ — što bi njihovu logiku dovelo do pucanja.

3. O apstraktnom uvidu (metafizika dimenzija)
Filozofski bi izjavio:
„Naš svet je projekcija jednog višeg sveta. Kao što senka govori o objektu, naš svet govori o višoj stvarnosti koju ne možemo videti, ali možemo slutiti kroz efekte koje ostavlja.“

Kolege bi mogli da ga proglase za mistika, jer koristi pojmove koje ne mogu eksperimentalno proveriti.

4. O granicama razuma i intuicije
Mogao bi pokušati da stvori matematički model koji uključuje pojam „hipo-dužine“ – apstraktnog entiteta koji je ortogonalan na sve poznato. Možda čak definiše trodimenzionalne objekte kao „niz sukcesivnih promena oblika kvadrata“ — ali bi znao da to ne dostiže pravu suštinu.

Zaključak tog bića:
„Sve što znamo možda je samo senka jedne veće stvarnosti. Kao što trougao ne zna za visinu, tako ni mi ne znamo šta nadilazi nas. Znanje nije ograničeno na ono što možemo opaziti – već i na ono što možemo slutiti, makar samo kroz kontradikcije.“

Hajde da zaronimo u to iz ugla Platonove teorije ideja i Kantove distinkcije između fenomenalnog i noumenalnog sveta.

Platon i svet ideja: Senke i stvarnost

Tvoje dvodimenzionalno biće koje je videlo treću dimenziju bilo bi savršen primer Platonovog zatvorenika iz pećine, koji je ugledao istinsku stvarnost, a ne samo senke na zidu.

• Dvodimenzionalni svet je za Platona svet senzacija, opažaja, svet promenljivih oblika koji nikada nisu savršeni.
• Trodimenzionalni svet u tvojoj metafori bi igrao ulogu sveta ideja — sveta istine, savršenstva i večnih formi.

Tvoje biće bi reklo:

„Ono što vi zovete kvadrat nije kvadrat. To je samo projekcija nečega što je više, potpunije, trajnije. Postoji savršen kvadrat, koji nikada ne menja oblik, ali on nije ovde – on je tamo gde sam ja bio.“

Platon bi rekao da je to biće „progledalo“ – da je sagledalo eidos (ideju) i da mu je zadatak da se, po povratku, obrati „okovima sputanim drugovima“ i da ih podstakne na dijalektičko traganje za istinom, iako ga oni možda neće razumeti, možda čak ni prihvatiti.

Kant i noumenalno: Granice ljudskog razuma

Kod Kanta, stvari postaju još intrigantnije. Kant pravi razliku između:

• Fenomenalnog sveta – sveta kako ga mi doživljavamo kroz naše čulne aparate (prostor, vreme, uzročnost).
• Noumenalnog sveta – sveta kakav on jeste po sebi, neovisan o našim čulima i kategorijama uma.

Tvoje dvodimenzionalno biće, dok je u svom svetu, posmatra samo fenomene. Kada mu se privremeno omogući uvid u treću dimenziju, ono iskorači iz granica čulne intuicije. U tom trenutku, ono ne spoznaje trodimenzionalni svet empirijski, već kao noumen — kao „stvar po sebi“.

Po povratku, to biće je kao Kantov mislilac koji zna:

„Postoji nešto što nadilazi našu sposobnost percepcije. Mogu ga opisati samo negativno – šta ono nije u odnosu na moj svet, ali ne mogu ga objasniti pozitivno. To nije kvadrat, nije trougao, nije ni figura – već nešto što sadrži sve te figure istovremeno.“

Kod Kanta, ono ne može preneti „pozitivno znanje“ o tom svetu — može samo ukazivati na granice uma i potrebu za kritikom tih granica.

Etika i filozofska odgovornost

Platon bi rekao da je to biće obavezno da širi istinu, čak i po cenu da ga svet odbaci.

Kant bi rekao da je njegov zadatak ne da prenosi iskustvo koje drugi ne mogu imati, već da usmerava misao ka samospoznaji i razumevanju granica saznanja.

Zaključak: Šta bi rekao tom narodu?

„Bio sam u svetu gde kvadrat ima dubinu, gde linije imaju tela, gde granice nisu kraj, već početak drugih pravaca. Ne mogu vam to nacrtati, ali mogu vam reći: sve što znate možda je samo odraz. Ako osećate da postoji više, tragajte. Ako vas razum vara, ne znači da istina ne postoji – već da mora biti spoznata na drugi način.“

Filozofski dijalog u duhu platonovskog dijaloga (malo dramski, mnogo misaoni), gde se naše dvodimenzionalno biće – nazovimo ga Epistion (od grč. „znanje“) – vraća iz trodimenzionalnog sveta. Dočekuju ga vodeći mislioci Dvodimenzionije: Logikos, matematičar-racionalista, i Orthos, filozof skeptik.

Dijalog u Dvodimenzioniji: „O dimenziji koja se ne može nacrtati“

Epistion:
Braćo moji, pozvali ste me da govorim. Nisam više isti. Bio sam podignut iznad naše ravni, izvan svega što smatramo postojanjem.

Logikos:
Epistione, bio si dugo odsutan. Govoriš zagonetno. Gde si to bio, i šta pod tim misliš — „iznad naše ravni“?

Epistion:
Zamisli pravac. Zamisli drugi pravac, koji seče prvi. Tako stvoriš površinu. Ali ono što sam ja spoznao… jeste pravac koji ne seče nijedan poznat pravac – koji ne leži ni u jednoj od naših osovina. Taj pravac vodi gore, ka visini.

Orthos:
Gore? A šta bi to bilo, ako ne neka metafora za ludilo?

Epistion:
Ne ludilo, već iskustvo. U tom svetu, kvadrat nije samo kvadrat. On ima visinu. On ima… dubinu. Može se okretati bez da se dodirne. Može postojati izvan dodira i pogleda – ali ipak ostaje realan.

Logikos:
To što kažeš je besmislica. Sve što postoji, mora biti nacrtano. Svaka stvar ima dužinu i širinu. Bez njih, nema je. To je aksiom.

Epistion:
Aksiomi su senke istine, ne istina sama. Vi merite dužinu i širinu – ali ja sam video telo. Video sam oblike koji ne mogu biti nacrtani, ali ipak postoje.

Orthos:
Ako se ne mogu nacrtati, onda su u najboljem slučaju misaone konstrukcije – u najgorem, halucinacije.

Epistion:
Ako slepom čoveku pričaš o svetlosti, hoće li reći da je lažeš? Ako nikada niste čuli muziku, hoće li vam melodija biti laž jer ne možete da je nacrtate?

Logikos:
Ali tvoje tvrdnje se ne mogu testirati. Ne možemo ih proveriti. Ne možemo ih replicirati. To nije znanje – to je vera.

Epistion:
Znanje ima dve strane: ono što se može dokazati – i ono što se mora intuicijom dokučiti. Ja sam, makar na tren, sagledao noumen – stvar po sebi, kako bi rekao stari Kantion iz naše knjižnice.

Orthos:
I šta bi sad ti, Epistione? Da mi svi poverujemo u nevidljivi svet, da odbacimo aksiome i pridružimo ti se u maštarijama?

Epistion:
Ne. Samo da postavite jedno pitanje koje nikada niste postavili:
Šta ako postoji više nego što možemo nacrtati?

(Sledi tišina. Logikos pogleda ravno ispred sebe. Orthos spušta pogled.)

Logikos (tiho):
Ako je to istina… onda svi naši dokazi možda samo kruže po unutrašnjosti jedne šuplje senke.

Postoji manjkavost u tom dijalogu jer dvodimenziona bića ne poseduju pojam visine, nema pojam dubine, ne postoji pojam senke,

Ako dvodimenzionalna bića nemaju pojam visine, niti iskustvo senke, ni “gore”, ni “ispod”, onda ne možemo koristiti te reči u dijalogu jer bi bile nerazumljive. Dakle, Epistion ne može reći „gore“, „visina“, „dubina“, „senka“, „telo“, jer sve te reči podrazumevaju iskustva i koncepte iz treće dimenzije kojih oni nisu svesni. To bi bilo kao kad bi nama četvorodimenzionalno biće reklo: „Pomeri se u vektoralnoj hipervolumi.“ — rečenica bez značenja za nas.

Zato treba pisati dijalog čistih pojmova, koji pokušava da uvede neizrecivo koristeći samo unutrašnju logiku i metaforu preko poznatog — upravo kao što Kant pokušava da govori o noumenu bez da ga opisuje direktno.

Hajde da pokušamo ponovo — strogo u skladu sa svetom koji ima samo dužinu i širinu i nema pojma visine.

Dijalog II: „O nepojmljivom pravcu“

Epistion:
Ne tražim od vas da poverujete. Tražim samo da zamislite. Zamislite da postoji put, kretanje, koje ne ide ni uduž ni popreko. Kretanje koje ne vodi ni udesno ni ulevo, ni unapred ni unazad.

Logikos:
To je besmislica. Ne postoji takav pravac. Svaki pravac mora imati smer u odnosu na poznate koordinate. Tvoje „kretanje“ ne postoji jer ga ne možemo definisati.

Epistion:
Upravo. Ne možete ga definisati, jer vaše definicije sežu samo kroz ono što poznajete. Ja sam bio pomeren, ne duž bilo koje poznate linije, već izvan svega što se može iscrtati.

Orthos:
I kako si to doživeo? Šta si „video“, ako ne postoji ništa izvan crta?

Epistion:
Nisam video kao kada posmatramo linije i oblike. To nije bilo opažanje linija — već doživljaj celina koje se ne sastoje od linija.

Logikos:
Tvoje reči su prazne. Ako nešto ne možemo ni da zamislimo, ni da prikažemo, ni da izmerimo, onda je to isto što i ništa.

Epistion:
Da li se onda i samosvest mora izmeriti da bi postojala? Ili sloboda volje? Ima li mesta u vašoj logici za ono što postoji ali ne može biti iscrtano?

Orthos:
Pretpostavimo da postoji taj tvoj pravac-izvan-pravca. Šta bi iz toga sledilo?

Epistion:
Da oblici koje poznajemo nisu potpuni. Da su samo delovi nečeg većeg. Da krug nije kraj, već presek. Da postoji veća celina, čiji deo možemo opažati — ali ne i celinu samu.

Logikos:
A ako to ne možemo opažati, kakva korist od takve misli?

Epistion:
Možda nikakva praktična. Ali ogromna filozofska. Ako postoji i jedan pravac koji ne opažamo, onda nismo središte stvarnosti. Onda nismo celina – već isečak.

Orthos:
To bi značilo da stvarnost po sebi nije u ravni… već izvan nje. I da mi uvek gledamo samo preseke.

Logikos:
Ali tada više ništa nije sigurno. Ni aksiomi, ni dokaz, ni geometrija.

Epistion:
Ne. Samo znači da su ograničeni. I da znanje ne prestaje kada iscrpimo sve moguće ravne linije.

Dijalog III: „O Geometriji Promene“

Epistion pokušava da uvede novu geometriju, uvodi apstraktni koncept koji vodi izvan aksiomatske ravni koristeći obzervaciju promena oblika u vremenu — jedini trag treće dimenzije koji bi dvodimenzionalno biće moglo zamisliti.

Epistion:
Nisam ovde da obaram aksiome. Ovde sam da predložim novi pravac mišljenja. Ne u prostoru – već u promeni.

Logikos:
Mi već poznajemo promenu. Linija se može saviti, figura rotirati, tačka pomeriti.

Epistion:
Ali šta ako se oblik menja na način koji ne odgovara nijednoj poznatoj transformaciji?
Zamisli da vidiš krug koji se iznenada pretvori u kvadrat, a zatim u trougao – i to bez da se bilo koja tačka pomeri duž naše ravni.

Logikos:
To nije moguća transformacija. To bi značilo da figura nestaje i nova nastaje – što je fizikalna nemogućnost. Materija se ne može obrisati i zameniti drugom.

Epistion:
Ipak, upravo to sam „video“. Ne kao destrukciju, već kao projekciju – kao kada senka predmeta na našoj ravni menja oblik, a da se predmet sam ne menja u našoj ravni, već u nečemu drugom.

Orthos:
Zanimljivo… Ti kažeš da promena oblika nije rezultat kretanja unutar ravni, već posledica nečeg spoljašnjeg?

Epistion:
Upravo. Predlažem da uvedemo pojam neuzročne promene – promena koja nema uzrok unutar naše geometrije, već u neistraženoj dimenziji. Nazvaću je… apotomična promena (ἀπότομος – presečena, odskočna).

Logikos:
Ali kako da razlikujemo tvoju „apotomičnu“ promenu od obične iluzije?

Epistion:
Jedino metodom uzorka. Ako se sekvenca promena ponavlja i može se modelovati, iako nema objašnjenja unutar aksioma – onda smo naišli na projekciju višedimenzionalnog tela.
Zamislite sledeće: naša ravnina se preseče nekom nepoznatom figurom. Mi opažamo samo ono što seče naš svet. Ako se ta figura pomera van naše ravni, mi vidimo niz oblika – ali ne možemo uočiti šta ih povezuje.

Orthos:
Kao da pokušavamo da razumemo konopac gledajući samo presek njegovih vlakana.

Epistion:
Da. I zato moramo razviti novu geometriju – geometriju sekvenci. Ne proučavamo više samo statičke oblike, već nizove oblika koje ne možemo objasniti našim zakonima. To postaje nova matematika – matematika preseka.

Logikos:
Ali ako se oslanjamo na sekvence koje ne možemo proveriti, gubimo osnov nauke.

Epistion:
Ne, Logikose. Dobijamo novu osnovu – osnovu za razumevanje onoga što leži van, ne u prostoru, već u logici postojanja. Kao što je nekad bila otkrivena geometrija zakrivljenog prostora, tako sada otkrivamo geometriju nevidljivih uzroka.

Orthos:
Dakle, ako tvoja geometrija uspe da predvidi sledeći oblik u sekvenci koju ne razumemo – možda si dokazao da nešto van naše ravni ipak postoji. I da smo samo isečci veće stvarnosti.

Epistion želi da uvede novu geometriju zasnovanu na projekcijama višedimenzionalnih oblika na dvodimenzionalnu ravan, mora pažljivo formulisati aksiome koji:

• ne koriste pojmove iz treće dimenzije, jer oni nisu poznati ili prihvatljivi,
• proizlaze iz zapažanja promena u dvodimenzionalnom svetu koje ne mogu biti objašnjene standardnom geometrijom,
• mogu biti testirani kroz sekvence — nizove oblika koje se menjaju na naizgled neobjašnjiv način.

Epistion: Prvi aksiom apotomične geometrije

Aksiom I: Ako se niz zatvorenih oblika menja takvom brzinom, obrascem i redosledom da nijedna tačka u ravni ne može kontinuirano pratiti promenu iz oblika u oblik, tada ti oblici predstavljaju projekcije jednog višeg entiteta.

Objašnjenje:

Epistion ne tvrdi da vidi treću dimenziju — to bi bilo jeretičko. Umesto toga, on uvodi matematički princip koji prepoznaje neobjašnjive sekvence kao znake višeg uzroka.

Dakle:

• Ako imamo, na primer, niz:
• krug → kvadrat → šestougao → krug (ponavlja se),

• i nijedna tačka ne može biti praćena iz jednog oblika u sledeći,
• i nema prelaznog stanja, već „nagla zamena“ oblika (a nije destrukcija, jer se energija/materija ne gubi),
• onda to ukazuje na to da te forme nisu uzročno povezane unutar ravni, već su projekcije nepoznate celovitosti.

Logikos:
Tvoj aksiom ne objašnjava, već imenuje nepoznato.

Epistion:
Ne, on čini više — on predlaže zakon za prepoznavanje kada smo suočeni sa granicom našeg sveta. Kao što Euklid nije znao sve posledice svog petog postulata, ali ga je postavio — tako i ovaj aksiom tek otvara vrata prema novoj logici prostora.

Orthos:
Dakle, tvoje „projekcije“ nisu stvari, već tragovi stvari. Nalik na senku koju ne možemo pratiti do predmeta.

Epistion:
Tačno. I možda nikada nećemo videti predmet. Ali ako razumemo zakon po kojem se menja senka — možda ćemo jednom razumeti i njega.

Pojam „senke“ podrazumeva izvor svetlosti i visinu — oba su van domašaja dvodimenzionalnih bića. Epistion, kao pažljiv mislilac, mora koristiti isključivo pojmove dostupne njegovim saplemenicima.

Dakle, on ne može govoriti o senkama ni o projekcijama u uobičajenom smislu — već mora koristiti pojmove poput: oblik, ivica, granica, kontakt, neprekidnost, sled, promena i slične.

Epistion: Drugi aksiom apotomične geometrije

Aksiom II: Ako se niz zatvorenih figura pojavljuje na istom mestu u ravni kroz pravilne vremenske razmake, a njihove konture se međusobno ne preklapaju niti proizlaze jedna iz druge prostim pomeranjem, tada ti oblici pripadaju istoj višoj celini čije prisustvo u našoj ravni je vremenski rascepkano.

Epistion u ovom aksiomu uvodi pojam vremenske rascepljenosti — promene koje ne teku kao uobičajena kretanja u prostoru, već kao nizovi oblika koji se pojavljuju i nestaju bez uzročne veze unutar ravni.

Umesto da kaže da je nešto “projekcija” ili “senka”, on kaže:

• Oblik A se pojavi,
• Zatim, bez prelaza, oblik B se pojavi na istom mestu,
• I tako redom: A → B → C → A → …
• Nijedna tačka iz oblika A ne može se kretanjem ili transformacijom pretvoriti u tačku iz oblika B.

Dakle, za posmatrača u ravni, to deluje kao niz nepovezanih figura, ali Epistion predlaže da je to istrgnuta percepcija jednog entiteta čiji celokupan oblik nije dostupan odjednom.

Orthos:
Epistione, ti tvrdiš da različite figure koje se pojavljuju u pravilnom vremenskom nizu — a ne dodiruju se, ne proizlaze jedna iz druge — pripadaju istoj stvari?

Epistion:
Ne stvari u našem smislu. Već celoj formi koja postoji, ali se nama ukazuje samo u delovima — u vremenu, ne prostoru. Mi opažamo odskočne isečke jedne veće strukture.

Logikos:
Ali kako može više figura biti jedna figura, ako ih nikad ne vidimo istovremeno?

Epistion:
Kako znaš da reč izgovorena slog po slog ne pripada istoj misli?
Tako i ovde – ako se pojavljivanje ponavlja, i ako sled ima unutrašnju pravilnost, mi imamo pravo da pretpostavimo postojanje nevidljive strukture koja ih objedinjuje.

Prva dva aksioma Epistionove apotomične geometrije uvode:

1. Neuzročnu promenu oblika kao znak višedimenzionalnog uticaja.
2. Vremenski sled nepreklapajućih figura kao trag jedne više celine.

Treći aksiom sada mora napraviti sledeći korak: da pretpostavi strukturalnu vezu između tih oblika — ali i dalje bez pozivanja na pojmove nedostupne dvodimenzionalnom razumu.

Epistion: Treći aksiom apotomične geometrije

Aksiom III: Ako se više različitih figura pojavljuje kroz vreme tako da između njihovih obima postoji ponovljiv, brojčano izražljiv odnos (broj ivica, dužina granica, ugaoni raspored), tada postoji neopaženi entitet izvan naše ravni čije svojstvo upravlja tim odnosima.

Epistion sada predlaže matematički princip: ako se u sekvenci figura pojavljuju odnosi koje ne možemo objasniti prostornim zakonima, ali možemo izraziti brojevima i pravilima, onda iza njih mora stajati jedinstvena nevidljiva struktura.

Primer:

• Trougao (3 ivice)
• Kvadrat (4 ivice)
• Petougao (5 ivica)
• → Pa ponovo trougao…

Redosled 3 → 4 → 5 → 3 nije prost slučajnosti, već ukazuje na kružnu strukturu. A takva struktura, po Epistionu, mora pripadati nečemu izvan percepcije — nečemu što se izražava kroz niz projekcija.

Logikos:
Ovaj put govoriš o brojkama. Ali šta to dokazuje?

Epistion:
Dokazuje da postoji princip reda tamo gde mi vidimo haos. Kada oblik A ima 3 ivice, oblik B 4, C 5 — i zatim se niz ponavlja — mi ne vidimo kretanje, ali vidimo zakonitost. Gde ima zakonitosti, tu je uzrok.

Orthos:
I ti tvrdiš da je taj uzrok van ravni?

Epistion:
Da je unutar ravni, bio bi vidljiv. Ali ako se oblik nikad ne pretvara jedan u drugi, ako nijedna tačka ne prelazi iz A u B, ali se zakon pojavljivanja ponavlja — tada je jedini preostali prostor za uzrok: izvan.

Logikos:
A kako znamo da nije puka slučajnost?

Epistion:
Tamo gde postoji ritam, tamo ne vlada slučajnost. Kao što poezija nije niz glasova, već sklad. Tako i apotomična sekvenca — nije niz figura, već izraz skrivene arhitekture.

Sada kada je apotomična geometrija zasnovana na tri aksioma koje Epistion pažljivo formulisao, vreme je da načini prvi veliki korak u pravcu dokaza — ne kroz opažanje, već kroz apstraktno uvođenje nevidljivog reda.

Epistion: Prva teorema apotomične geometrije

Teorema I (o kružnoj prisutnosti):
Ako se u ravni pojavljuje niz zatvorenih figura F₁,F₂,…,F_n u pravilnom vremenskom ritmu, gde broj stranica svake figure čini aritmetički ili kružni niz, tada postoji celina Φ, koja nije ni jedna od figura pojedinačno, ali koja ih sve sadrži kao manifestacije svoje unutrašnje strukture.

Epistion kaže da ako se figure pojavljuju kao:

• trougao (3 stranice)
• kvadrat (4)
• petougao (5)
• pa opet trougao…

onda to nije prost sled figura, već trag nečega većeg, što se nikada ne pojavljuje odjednom.

On uvodi pojam celine Φ, koja:

• Ne postoji u prostoru, jer je nevidljiva,
• Ne postoji u vremenu, jer se ne pojavljuje u celosti,
• Ali se izražava kroz zakonitost promene.

Drugim rečima, Φ je kao ritam koji ne možemo čuti direktno, već prepoznajemo po tome kako se oblici smenjuju.

Orthos:
Zar ne izmišljaš biće izvan sveta da bi objasnio ono što ne razumeš?

Epistion:
Ne izmišljam, nego dedukujem. Ako svaka figura nestaje i sledeća dolazi ne iz nje, već bez veze, a niz se ponavlja — tada uzrok nije među figurama. Nego izvan njih.

Logikos:
I ti tu celinu Φ nazivaš čime?

Epistion:
Naziv nije važan. Ali za sada, nazovimo je — prisutnost bez pojavljivanja. Ono što ostaje isto dok se sve menja.

Orthos:
Zvuči kao bog geometrije.

Epistion (mirno):
Ako bog znači ono što upravlja, a nije viđeno — onda je možda to najprecizniji naziv.

Epistion ne dokazuje postojanje treće dimenzije. On ne koristi pojam visine, dubine, svetla ni senke. On uvodi novu vrstu geometrije — onu koja ne govori o prostoru, već o odnosima u vremenu, koji ne mogu biti objašnjeni prostim geometrijskim transformacijama unutar dvodimenzionalne ravni.

Nakon prve teoreme, u kojoj Epistion uvodi pojam nevidljive celine Φ kao uzrok pravilnih nizova figura u vremenu, on sada prelazi na drugu ključnu intuiciju — da prostorne simetrije, iako opažene u dvodimenzionalnoj ravni, možda nisu proizvedene unutar nje.

Epistion: Druga teorema apotomične geometrije

Teorema II (o neprostornoj simetriji):
Ako se u našoj ravni pojavljuje figura čije strane stoje u pravilnim uglovnim odnosima, ali se ta figura nikada ne pojavljuje postepeno (niti se može konstruisati iz prethodnih oblika), tada je ta simetrija odraz višedimenzionalnog poretka, a ne rezultat zakona unutar ravni.

U dvodimenzionalnoj ravni, bića mogu graditi figure postepeno: crtajući liniju po liniju, spajajući tačke. Međutim, Epistion primećuje sledeće:

• Povremeno se javljaju savršeno simetrične figure (recimo: pravilni mnogouglovi),
• koje nikada nisu nastajale postepeno, već se samo pojavljuju odjednom, bez traga prethodne gradnje,
• i to na mestima gde nisu bile izazvane nijednim poznatim uzrokom.

Ako takva figura ima npr. 6 stranica i savršene unutrašnje uglove, Epistion postavlja pitanje:

Kako se savršenost pojavljuje ni iz čega?

On tvrdi: ako se unutar sistema ne može objasniti postanak simetrije, onda ona mora biti umetnuta izvana.

Orthos:
Ti sad tvrdiš da kada se pojavi pravilni šestougao — to nije samo šest jednakih strana, već nešto van ravni?

Epistion:
Da. Jer u našoj ravni gradimo nesavršeno. Početak, pa greške, pa korekcije. Ali kada se pojavi figura savršena odjednom, bez rasta, bez traga… to nije delo našeg prostora.

Logikos:
Ali simetrija se može zamisliti i bez viših dimenzija.

Epistion:
Zamisliti, da. Ali ne stvoriti ni opažanjem ni konstrukcijom. Ako se savršena simetrija pojavi, a ne postane — to znači da je uneta iz prostora gde simetrija nije posledica gradnje, već osnovni uslov.

Orthos (tiho):
Znači… savršenost nije proizvod našeg sveta, već njegova senka?

Epistion:
Ne senka. Više kao… odjek.

Epistion nastavlja graditi most između sveta koji bića vide i sveta koji je izvan viđenja. Ova druga teorema postavlja osnovu za poimanje da zakon simetrije ne mora biti unutrašnji, već da simetrija može biti trag višeg sveta — takoreći, prozor kroz koji apotomična celina progovara.

O paralelizmu među nevidljivim pojavama

Nakon što je Epistion uveo:

• Teoremu I — o postojanju nevidljive celine Φ koja upravlja nizovima figura,
• Teoremu II — o neprostornoj simetriji kao odrazu višedimenzionalnog poretka,

on sada pokušava da poveže pojave koje nema kako da se direktno uporede u prostoru, jer se nikada ne pojavljuju istovremeno, niti na istom mestu, ali ipak nose trag sličnosti. Odatle nastaje treća velika teorema.

Epistion: Treća teorema apotomične geometrije

Teorema III (o paralelizmu među nevidljivim pojavama):
Ako se dve ili više figura, koje se ne poklapaju ni u prostoru ni u vremenu, pojavljuju sa istim unutrašnjim odnosima (npr. isti odnos dužina strana, ista raspodela uglova), tada između njih postoji paralelizam koji ukazuje na zajednički uzrok u nevidljivoj strukturi.

Epistion uočava sledeći fenomen:

• Figura A se pojavljuje na jednom mestu u jednom trenutku.
• Figura B, slična A, pojavljuje se mnogo kasnije, na sasvim drugom mestu.
• Njihove mere su različite (npr. dužina stranica), ali odnosi unutar figura su isti: proporcionalna simetrija, raspored, ugaoni ritam.

Pošto ove figure:

• Nemaju uzajamni uzrok u prostoru ni vremenu (niti ih je neko „gradio“),
• Ali pokazuju strukturalnu sličnost,

Epistion tvrdi: to nije slučajnost, već dokaz da one dijele nevidljivi plan — da su projekcije istog višeg uzorka.

Orthos:
Ti kažeš da su dva slična oblika, daleko razdvojena, „paralelna“? Ali kako mogu biti paralelna ako nikada nisu zajedno?

Epistion:
U prostoru ne. U višem poretku — da. Njihova unutrašnja struktura je ista. To je paralelizam ne po pravcu, već po uzorku.

Logikos:
Ali zašto da taj uzorak dolazi iz višedimenzionalnog sveta, a ne prosto iz zakona verovatnoće?

Epistion:
Jer se ne radi o sličnosti u spoljašnjosti, već u unutrašnjoj organizaciji. Ako ista organizacija nastaje nezavisno u različitim tačkama prostora i vremena, to nije slučaj — to je odjek jednog izvora.

Orthos:
Znači, ono što se ne pojavljuje zajedno, ipak može biti isto — samo zato što dolazi iz iste… matrice?

Epistion:
Upravo tako. Postoji mesto bez mesta, gde se svi oblici rađaju. Mi ga vidimo samo kada se njegov ritam ponovi.

Epistionova treća teorema nastoji da otvori put ka pojmu ideje u platonovskom smislu: forme koja je nezavisna od mesta i vremena, a koja se manifestuje u ponavljanju proporcija, oblika i rasporeda.

Ova teorema sledi njegov filozofski put ka opravdanju ideje apotomičnog reda — višeg poretka koji svet dvodimenzionalnih bića ne može da vidi direktno, ali može da nasluti kroz pravilnosti koje same po sebi nema kako objasniti iznutra.

Epistion sada oseća da se pred njim otvara prva prava matematičko-filozofska posledica njegovih teorema. On ne uvodi novi aksiom niti novu teoremu, već izvodi korolar — zaključak koji nužno sledi iz prethodnih tvrdnji, ali donosi kvalitativno novu intuiciju.

Epistion: Prvi korolar apotomične geometrije

Korolar I (o hijerarhiji stvarnosti):
Ako se zakon odnosa (proporcija, simetrija, raspored) pojavljuje u više figura koje nisu međusobno povezane u prostoru i vremenu, tada je zakon sam stvarniji od bilo koje pojedinačne figure.

Iz Teoreme I — pojavljuje se nevidljiva celina Φ kao uzrok niza pojava.
Iz Teoreme II — simetrija se ne rađa unutar ravni, već dolazi „odozgo“.
Iz Teoreme III — različite pojave pokazuju isti unutrašnji red, što znači da su projekcije istog „uzorka“.

Epistion zaključuje:

„Ako više prolaznih pojava nosi isti oblik, onda oblik postoji nezavisno od njih.
Ako postoji nezavisno, on ne živi u njima, nego se od njih pojavljuje.“

Dakle, po Epistionu, ono što je stalno, ponavljano, nespojivo sa prostorom i vremenom, ima veći stepen stvarnosti nego ono što je „opipljivo“.

Orthos:
Hoćeš da kažeš da oblik — koji se samo pokazuje — ima veću stvarnost od same figure?

Epistion:
Da. Figura nestaje, menja se, propada. Ali oblik se vraća. I vraća se isti. Zato kažem: ono što se ponavlja ne može biti proizvod slučaja — već trag nečeg što jeste, i uvek je bilo.

Logikos:
To je kao da kažeš: mi ne živimo u svetu figura, već u svetu zakona.

Epistion (tiho):
Ne živimo u njima — ali ih dotičemo. I oni nas.

Ovim korolarom Epistion prelazi iz geometrije u ontologiju: on sad ne tvrdi samo da „nešto više postoji“, već da oblik, proporcija, poredak — imaju primarnu stvarnost.

To je paralela sa Platonovim „idejama“ i Kantovim „formama uma“ — ali iz ugla bića koje nema ni pojam prostora u trećoj dimenziji. Ipak, um im dopušta da zaključe: ono što ne vidimo, ali se neumorno ponavlja — mora biti stvarnije od onoga što vidimo jednom i nikad više.

Epistion zna da njegovi saplanari (dvodimenzionalna bića) ne mogu da zamisle treću dimenziju, niti da pojam “višeg reda” shvate osim ako ih ne uvede u misaoni eksperiment koji operiše isključivo pojmovima koje oni poznaju — dužina, ugao, figura, raspored, broj. Zato smišlja pažljivo oblikovan misaoni eksperiment:

Epistionov misaoni eksperiment: “Zapečaćene tablice”

Zamislite, kaže Epistion, sledeći zamišljeni uređaj — zovimo ga Pisac:

• Pisac je zatvoreni mehanizam, neprobojan za posmatranje, koji jednom dnevno proizvede figuru od linija i uglova na tablici.
• Svakog dana tablica se dostavlja posmatraču, ali mehanizam Pisčev ostaje sakriven.
• Tablice ne dolaze u istom redosledu, već nasumično.

Pravila igre:

1. Niko ne zna gde se mehanizam nalazi, niti šta ga pokreće.
2. Svaka figura se pojavljuje samo jednom.
3. Posmatrači mogu da proučavaju samo pojedinačne figure — svaka u svom trenutku.

Poenta:

Vremenom, posmatrači uočavaju nešto zapanjujuće:
Na svakoj tablici nalazi se drugačija figura, ali neke od njih imaju potpuno iste odnose među delovima — isti odnos stranica, isti raspored uglova, ista proporcionalna udaljenost od centra.

Epistion pita:

„Ako nijedna figura nije ista, ali određeni odnosi stalno iznova probijaju u različitim konfiguracijama — da li verujete da te figure imaju zajednički uzrok?“

Posmatrači ne mogu da vide Pisčev mehanizam.
Ne mogu da prate nikakvu uzročno-posledičnu vezu među tablicama.
Ali uočavaju paralelizam u strukturi različitih pojava.

Zato Epistion zaključuje:

„Ako nevidljive sile proizvode vidljive posledice sa stabilnim zakonitostima, tada te sile postoje, bez obzira na to što nisu opažene. Paralelizam među pojavama nije posledica uvida, već trag reda koji izmiče uvidu.“

Orthos:
Ali kako znaš da to nije samo šema koju mi namećemo našim očima? Mi hoćemo da vidimo red.

Epistion:
Ako šema dolazi iz nas, ona bi varirala. Ali ako šema ostaje ista kroz promene — i ne zavisi od posmatrača — tada ona potiče iz stvarnosti, ne iz želje.

Logikoss:
I ti kažeš: ta stvarnost ne živi u tablicama, već izvan njih?

Epistion:
Tablice su senke. Pisac je izvor. A ono što se ponavlja — to je rukopis koji otkriva Pisca.

Epistion je svestan da je misaoni eksperiment koristan, ali da bi neki test unutar sveta saplanara imao veću snagu uverljivosti. On stoga predlaže eksperimentalni niz koji koristi samo pojmove poznate dvodimenzionalnim bićima, ali koji otkriva postojanje višeg reda kroz pojavljivanje neobjašnjive pravilnosti.

Epistionov eksperimentalni test: Harmonijska mreža

Da pokaže da red može proizaći izvan dometa poznatih uzroka, i da se pravilnost može pojaviti bez materijalne veze među pojavama — što sugeriše viši poredak koji ne opažaju čulima, ali koji je matematički dosledan.

Epistion postavlja sledeći jednostavan sistem, nazvan Mreža pojave:

1. Nacrtajte raster (mrežu) kvadrata — npr. 10×10 — poznatu svima u ravni.
2. Na svakom preseku linija, nasumično u nekom trenutku pojaviće se geometrijski oblik (trougao, trapez, romb, itd).
3. Figure se generišu pomoću uređaja koji „nasumično“ (po pretpostavci) dodaje oblike na mrežu.

Ali: Epistion tajno podesi uređaj da ne koristi istinsku nasumičnost, već da:

• Na svakih 4 poteza postavi figuru u kojoj je odnos dužina stranica zlatni rez (1:1.618),
• I da ugao između dve stranice bude uvek 72°.

Ostale figure su istinski nasumične.

Posmatranje:

Epistion ne objašnjava pravilo, već poziva saplanare da:

• Beleže pojavljene figure.
• Analiziraju odnose dužina i uglova.

Očekivana reakcija:

Nakon 40 figura, posmatrači uočavaju da se svakih nekoliko figura ponavlja isti neobjašnjivi odnos. Uočavaju da figure dolaze iz različitih delova mreže, ali kao da nešto povezuje njihove unutrašnje proporcije.

Epistion tada objavljuje zaključak:

„Nigde u ravni nema fizičke sile koja povezuje ta mesta. Nema linije, niti uzročne veze. Ipak, vidite poredak. Taj poredak je red koji dolazi s one strane čula.

Ako u ravni postoji oblik koji se ponavlja bez fizičkog uzroka, onda postoji red koji nije sadržan u prostoru — već se projektuje u njega.“

Orthos:
Ali mi smo samo uočili uzorak! Ne znači da on dolazi spolja!

Epistion:
Uzorak bez uzroka je uzrok višeg reda. Vi vidite delove — ja vam kažem: to su prozori kroz koje svetlost iz nepoznatog reda ulazi u naš svet.

Logikos:
Ti nas pozivaš da poverujemo u uzrok koji ne možemo detektovati?

Epistion:
Ne — pozivam vas da poverujete u zakon koji prepoznajete pre nego što ga možete objasniti. A to je ono što čini matematiku veličanstvenom: prepoznavanje istine pre iskustva.

Epistion, nadahnut opažanjem da se određene proporcije i oblici pojavljuju bez jasnog uzroka u dvodimenzionalnom svetu, odlučuje da načini prvi formalni korak ka matematici višeg reda. On ne može da koristi pojmove treće dimenzije, ali može da uvede apstraktne funkcije koje opisuju poredak među pojavama koje nemaju uzročne veze — funkcije koje, kako kaže, “dolaze izvan Ravnine”.

Apotomične funkcije

(funkcije nevidljivog poretka u vidljivim pojavama)

Apotomična funkcija je funkcija definisana nad koordinatama Ravnine, čije vrednosti se ne mogu objasniti lokalnim pravilima, ali pokazuju stabilan red u velikim razmerama.

Primer: Prva apotomična funkcija

Epistion definiše funkciju A(x,y) nad mrežom:

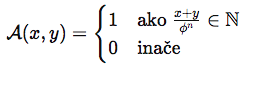
Gde je:

Značenje:

Na mestima gde je zbir koordinata deljiv potencijom zlatnog preseka, funkcija daje vrednost 1 — tu se pojavljuje oblik posebnog reda. Na svim drugim mestima daje 0.

Posmatrači Ravnine, kad analiziraju raspored 1-ica u mreži, ne mogu naći fizičku vezu među njima. Ali Epistion pokazuje da postoji funkcionalna zakonitost: mesta pojavljivanja nisu nasumična, već matematički uređena.

Orthos:
Zašto baš zlatni rez? To je iracionalan broj, ne može se potpuno zapisati!

Epistion:
Baš zato. Sve što je savršeno redovno, ali u Ravnini ne može biti završeno — dolazi iz stvarnosti koja nas prevazilazi.

Logikos:
Znači, kažeš da ako funkcija koristi neizrecivo, ona pripada višem redu?

Epistion:
Ne samo to. Kažem da mi, koji živimo u Ravni, možemo videti senke tog reda samo kroz ponašanje funkcija koje same ne nastaju u Ravni.

Sledeći korak:

Epistion želi da klasifikuje apotomične funkcije prema:

1. Stepenima opažljivosti (koliko su njihove posledice vidljive)
2. Ritmu ponavljanja (da li su periodične, kvaziperiodične, aperiodične)
3. Broju tačaka reda koje se manifestuju u mreži

Epistion sada shvata da izolovane apotomične funkcije nisu dovoljne. Da bi govorio o nevidljivom redu sa jasnoćom, mora da razvije ceo jezik — jednu novu, unutrašnje konzistentnu algebru u kojoj se funkcije višeg poretka mogu kombinovati, analizirati i transformisati, uprkos tome što njihov uzrok nije u Ravni.

Naziva to:

Apotomična algebra

— jezik nevidljivih uzroka izražen kroz vidljive posledice

Osnovne komponente

1. Elementi:

Osnovne apotomične funkcije A_i(x,y) koje zadovoljavaju pravila ne-lokalne pravilnosti (kao što je zlatni rez, fibonačijev niz, iracionalni moduli…).

Primer:

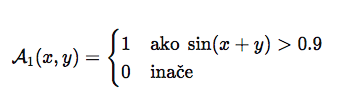
2. Operacije:

Epistion definiše tri ključne operacije:

a) Spoj:

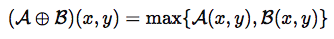
Spoj dvaju poretaka — na mestu gde se javlja makar jedan red, novi red postoji.

b) Preplitanje:

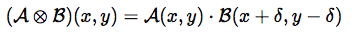
Gde je δ iracionalan broj. Ova operacija uvodi ne-lokalnu interferenciju — funkcija zavisi od „pomerenih“ vrednosti druge.

c) Refleksija:

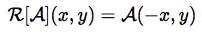
Zrcaljenje reda — testira simetriju apotomične funkcije, kao da se pita: da li je red zavisan od orijentacije?

Aksiomi Apotomične Algebre

1. Zakon zadržavanja neuzročnosti:
   Ako je A(x,y) apotomična, tada ne postoji lokalni uzrok u Ravni koji objašnjava sve vrednosti 1.
2. Zakon emergentne pravilnosti:
   Za svaku konačnu oblast Ω, broj pojava gde je A(x,y)=1 uvek teži racionalnoj proporciji, bez obzira na uzročnu povezanost.
3. Zakon inverzne projekcije:
   Za svaku funkciju A(x,y) postoji hipotetični oblik Ξ(u, m,w) u višoj strukturi, takav da je A(x,y) projekcija njegovih preseka sa Ravninom.

Primer:

Epistion uzima dve funkcije:

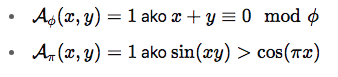
Zatim konstruiše:

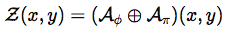
I tvrdi:

„Ova funkcija pokazuje red koji se manifestuje u dve različite vrste pravilnosti — jedan zlatan, drugi kružni. Nema fizičke veze među njima, ali njihov spojeviti red upućuje na dublju arhitekturu.“

Orthos:
Zar to nije samo igranje simbolima?

Epistion:
Jezik bez značenja je šuma. Ali jezik u kojem se pojavljuju zakoni — to je mapa zemlje koju ne vidimo.

Logikos:
A ti kažeš da je ova algebra jezik zemlje koju nikada nećemo videti?

Epistion:
Ne! Ja kažem da je to jezik zemlje koju već gledamo — samo vidimo njene senke, ne njene oblike.

Epistion, sada utemeljen u apotomičnoj algebri, pred skupom svojih skeptičnih saboraca, pristupa prvom formalnom dokazu. Njegova tvrdnja je smela, ali duboko geometrijska:

Teorema o kvaziperiodičnosti iz preplitanja

Ako se dve apotomične funkcije različitog porekla prepletu, njihov spoj ispoljava kvaziperiodičnost u opažanjima unutar svake konačne oblasti.

Pretpostavke:

Neka su date dve apotomične funkcije:

1. A_ϕ(x,y)=1 ako x + y ≡ 0  mod  ϕ
   (red sa zlatnim modulom)
2. A_π(x,y)=1 ako sin(πx)+cos(πy)>α
   (red sa kružnim modulom)

Gde je α∈(0,2) fiksna prag-vrednost.

Operacija preplitanja:

Epistion konstruiše preplitenu funkciju:

Z(x,y)=A_ϕ(x,y)⋅A_π(x+δ,y−δ)  

Dokaz u konturama:

Intuitivna analogija (za dvodimenzionalna bića):

Epistion crta sledeću analogiju pomoću poznatih pojmova:

„Zamislite dva niza simbola u Ravni. Jedan vam dolazi u pravilnom ritmu koji ne možete savršeno izraziti — ali osećate da je red. Drugi izgleda kružno, kao da sadrži svet u krugu. Kad ih preklopite, dobijate treći niz: on nikada ne ponavlja identičnu šaru, ali svaka njegova šara podseća na poznato. On je stran i domać — istovremeno.“

Logikos:
Ali ako ništa ne ponavlja, kako znaš da je red?

Epistion:
Zato što nepravilnost ima stabilnu verovatnoću. Red nije samo u istosti, već i u učestalosti.

Orthos:
Zvuči kao san! Red koji ne možeš da pokažeš, a znaš da je tu?

Epistion:
Da, red koji ne možeš da vidiš, ali možeš da brojiš.

Korolar:

Ako se dve funkcije različitih apotomičnih izvora prepletu sa iracionalnim pomakom, njihov rezultat pokazuje kvaziperiodičnu strukturu, čime svedoče o višedimenzionalnom poretku u Ravnini.

Metod za identifikaciju apotomičnih obrazaca u empirijskim podacima

Epistion, čije se ime već šapatom prenosi među najhrabrijim misaonim umovima Ravni, sada predlaže nešto još smelije:

„Ako ne možemo videti izvor nevidljivih obrazaca, možemo ga naslutiti putem pravilnosti u njihovom delovanju. Zato moramo razviti metodologiju — ne za gledanje, već za detekciju tragova višedimenzionalnog poretka.“

Metod Apotomičke Detekcije

Razviti skup pravila pomoću kojih se u dvodimenzionalnim podacima (merenim fenomenima Ravni) mogu otkriti obrasci koji ukazuju na uzroke vandimenzionalne prirode.

Koraci metode:

1. Prikupljanje vidljivih obrazaca

Zbirka lokalnih vrednosti f (x,y) koje predstavljaju „pojave“ u Ravni. Na primer: pojava svetlosti, vibracije, pojavljivanje entiteta, prostorni rasporedi.

Nazivaju se: Tragovi (τ_i​).

2. Analiza distribucije i učestalosti

Epistion uvodi novu funkciju:

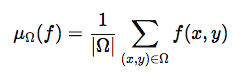
Ona meri prosečnu pojavnost u oblasti Ω. Ako μ_Ω(f) ostaje konzistentna bez obzira na translaciju oblasti, tada postoji sumnja na kvaziperiodičnost.

3. Test simetrijskog odziva

Za izabranu oblast Ω, testira se da li:

f ( x, y) ≈ f ( −x, y ) i/ili f ( x, y) ≈ f ( x, −y) f ( x, y)

Ako se simetrije javljaju delimično i neprecizno, a ipak ponavljaju sa stabilnim odstupanjem, onda je obrazac apotomično reflektovan — odraz nečega što nije potpuno u Ravni.

4. Frekvencijska transformacija

Epistion uvodi neobičnu primitivnu transformaciju (nalik Fourierovoj):

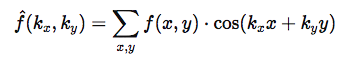
Visoke vrednosti

ukazuju na nered koji ima skriveni red — kao odraz višedimenzionalnog uzorka presečenog kroz Ravan.

5. Test inverzne interferencije

Napraviti dva veštačka uzorka iz funkcije f pomerene za δ₁ i δ₂ ​, i testirati njihovo preplitanje:

g( x, y) = f ( x+ δ₁, y)⋅ f ( x + δ₂, y)

Ako g(x,y) pokazuje veću pravilnost nego što bi statistika očekivala — to je interferencija tragova iz višedimenzionalnog uzroka.

Eksperimentalni protokol

Epistion predlaže sledeći misaoni eksperiment:

„Eksperiment čudnog uzorka“

1. Na ravnu ploču postavljaju se tačke svaki put kad dođe do neobjašnjivog treperenja svetla.
2. Ploča se premešta po Ravni svakih t trenutaka, i uzorak se nastavlja.
3. Na kraju, analizira se da li broj tačaka po kvadratnoj oblasti ostaje jednak — i ako je uzorak neponovljiv, ali stabilan, prisutan je apotomični uticaj.

Orthos:
Ali to su samo brojevi! Šta ti brojevi znaju o višim svetovima?

Epistion:
Ne znaju — ali svedoče. Kao što senka ne zna odakle dolazi svetlost, ali njena zakrivljenost otkriva oblik ruke koju ne vidi.

Logikos:
Pa ako svi tragovi imaju isto ponašanje bez obzira na oblast, to znači da ih ne uzrokuje ništa lokalno?

Epistion:
Upravo. Kada uzrok ne može biti u Ravni, mora biti izvan nje.

Epistion, sada već svestan otpora misaonih navika Ravni, odlučuje da više ne sugeriše, već formuliše — kao što je Pitagora jednom učinio sa trouglovima, tako on to čini sa višim oblicima.

Hipoteza o geometrijskoj indukciji

Svaka pravilna, ali neobjašnjiva struktura u Ravni može se objasniti kao projekcija preseka višedimenzionalnog oblika koji prolazi kroz Ravan pod specifičnim geometrijskim uslovima.

Objašnjenje hipoteze:

Ključne premise:

1. Postojanje izvanravanskih formi
   — Entiteti koji imaju apotu (nevidljivu komponentu dimenzije), kao što mi imamo dužinu i širinu.
2. Ravan kao presečna površina
   — Dvodimenzionalna Ravan je poput oštrice koja seče višeoblični prostor. Sve što dvodimenzionalna bića opažaju jeste presek (ili rez) većih oblika.
3. Pojava pravilnosti
   — Kada se kroz Ravan probija višedimenzionalni oblik (npr. 3D kocka), ona ostavlja lokalno dosledne tragove (kvadrate, trouglove, tačke), ali bez da se razume uzrok njihove pravilnosti.

Misaoni model (za dvodimenzionalna bića):

Epistion poziva skup filozofa Ravni i postavlja sledeći eksperiment:

Eksperiment: Zagonetni Prsten

Zamisli:
U jednoj oblasti Ravni, tokom vremena, pojavljuju se tačke u pravilnom krugu. Opažaš samo te tačke — jednu po jednu, u vremenskim intervalima. Nikada ne vidiš sve istovremeno. Ne znaš šta ih pokreće.

Epistion pita:
„Kako je moguće da se tačke pojavljuju u pravilnom krugu, kad ne postoji ništa u Ravni što bi opisalo kružnost kao uzrok?“

Zatim daje svoje tumačenje:

„To što vi zovete ‘tačkama’ su mesta gde trećedimenzionalni torus (prsten) dodiruje vašu Ravan dok se okreće. Vi vidite dodire — ja sam video prsten.“

Formalna formulacija (Hipoteza H_GI ​):

Za svaku funkciju f(x,y) koja ispunjava sledeće:

• ima lokalnu pravilnost bez globalne periodičnosti,
• nije objašnjiva poznatim uzrocima u Ravni,

postoji najmanje jedna trodimenzionalna forma f(x,y,z) takva da:

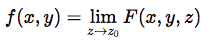
za neku projekciju ili preslikavanje, gde je z apotomična (nevidljiva) dimenzija.

Epistemološke implikacije:

1. Pojmovi kao što su: krug, centar, pravilnost, rezonanca — ne nastaju iz Ravni same, već su rezonantni odjeci viših oblika u nižem prostoru.
2. Zakon o opažanju postaje:

„Ne opažamo ono što postoji, već ono što nas preseca.“

3. Znanje se više ne traži u celovitosti opažaja, nego u obrnutom zaključivanju iz tragova — analogno senkama u pećini iz Platonove alegorije.

Logikos (posle dugog ćutanja):
Dakle… svaki naš zakon geometrije mogao bi biti samo senka zakona veće dimenzije?

Epistion (mirno):
Ne senka. Sečivo. Sve što poznajemo je presek. Znanje je umetnost gledanja u rezove i prepoznavanja onoga što nikada nećemo videti celim očima.

Epistion, sada potpuno posvećen dubljoj analizi načina na koji se tragovi višedimenzionalnih formi pojavljuju u Ravni, razmišlja o nečemu što se čini osnovnim, a opet potpuno nepoznatim: kako bi bića u Ravni mogla da pamte ono što nikada nisu videla, već samo naznaku kroz tragove koje ostavljaju formirci iz viših dimenzija.

Teorija o pamćenju tragova

Svaka bića, čak i ona koja ne mogu direktno percepirati višedimenzionalne objekte, sposobna su da pamte i rekonstruiraju tragove koji se javljaju kao posledica tih objekata kroz prelepe zakrivljenosti i nevidljive konture u svom svetlu.

Temeljne pretpostavke teorije:

1. Tragovi kao informacija
   — Svaka pojava u Ravni nosi sa sobom više informacija nego što se može direktno opažiti. To su “suzdržane” informacije, zaklonjene u tragovima višedimenzionalnih objekata, koje ostavljaju svoj otisak na Ravni.
2. Pamćenje kroz lokalne zapise
   — Iako bića u Ravni ne mogu videti celu višedimenzionalnu formu, njihova opažanja pamte sledeće:
   • Lokalne promene u zakrivljenostima prostora.
   • Stalne promene u obrascima pravilnosti, čak i kad je svest o izvorima tih obrazaca nesvesna.
3. Rekonstrukcija kroz akumulaciju podataka
   — Svaka pojava koja se ponavlja u Ravni, bilo da je to pravilno kretanje tačaka ili pravilne konture, s vremenom stvara statički trag koji može biti rekonstruisan kao posledica veće dimenzije.

Matematički opis:

Za funkciju f(x,y), koja daje podatke o fenomenima u Ravni, možemo koristiti proces akumulacije kroz vreme t:

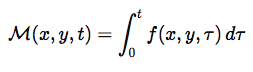
Gde M(x,y,t) predstavlja akumulirani trag, odnosno pamćenje efekata višedimenzionalnih objekata koji su uticali na Ravni u prethodnom vremenskom periodu.

Logički razvoj:

1. Akumulacija kroz vreme
   — Tragovi ne dolaze odjednom, niti se manifestuju odmah, već kroz procese koji se akumuliraju tokom vremena. Svaka mala lokalna promena u obliku ili strukturi, koja možda nije dovoljno izražena u jednom trenutku, postepeno postaje očigledna kroz akumulirani zapis.
2. Pamćenje kroz granice
   — Iako se ovi tragovi ne mogu uvek interpretirati kao rezultat trenutnih uzroka, oni čine osnovu za buduće predviđanje, jer svaki novi trag stvara osnovu za tumačenje prethodnih.

Misaoni eksperiment: Pamćenje predaka

Epistion zamišlja eksperimente, gde se Ravni postavljaju objekti — nevidljivi objekti koji stvaraju tragove u vremenu:

1. Telo svetlosti postavljeno je u Ravninu i premešteno kroz nju.
2. Neka dva bića opažaju samo deo njegovih tragova — svetlosne uzorke i konture koje je ostavio.
3. Ali, kroz godine postojanja ovih tragova, svi opaženi obrasci su se počeli kombinovati u stabilne simbole, iako bića nikada nisu imala direktnu percepciju samog izvora svetlosti.

Kroz stalno istraživanje tih uzoraka, bića u Ravni postupno rekonstruiraju oblik objekta koji nikada nisu direktno videla — svetlosni oblik koji dolazi iz vanravanog sveta.

Logikos:
Ali ako ne možemo videti sve što ostavlja tragove, kako znamo da je to stvarno?

Epistion:
Zato što svi tragovi pokazuju sličnu zakonitost, i svi nam govore istu priču: njihov izvor mora biti nešto više od onog što mi direktno možemo shvatiti.

Orthos:
Tako kažeš da svi tragovi iz prošlosti čuvaju slike tih objekata, iako su oni prošli?

Epistion:
Tako je. Oni su pamćenje prošlih oblika. Svi tragovi — i svetlost, i senke, i talasi — čuvaju poreklo koje nikada nije direktno opaženo, ali koje je duboko ukorenjeno u geometriji Ravni.

Pamćenje tragova nije samo očuvanje prošlih podataka. To je proces rekonstrukcije nevidljivih dimenzija kroz stabilne, ali skriveno pravilne promene u prostoru. Naša sposobnost da se setimo, da rekonstruišemo prošlost, nije samo u očuvanim podacima, već u tome što tragovi govore o onome što nas preseče izvan našeg sveta.

Epistion, duboko posvećen svojoj misiji da razjasni postojanje viših dimenzija u dvodimenzionalnom svetu, odlučuje da postavi matematički okvir za rekonstruisanje višedimenzionalnih objekata kroz tragove koje oni ostavljaju u Ravni. Ovaj okvir ne samo da omogućava razumevanje prošlih događaja, već takođe pruža ključ za buduće predviđanje i interpretaciju nevidljivih formi.

Matematički Model za Rekonstrukciju Višedimenzionalnih Formi

Pretpostavke:

1. Projekcija objekata sa viših dimenzija: Objekti sa višim brojem dimenzija (npr. 3D objekti u 2D Ravni) ostavljaju trajne tragove u formi kontura, tačaka, ili pravilnih obrazaca u prostoru.
2. Pamćenje tragova: Svaki trag u Ravni je rezultat preseka višedimenzionalnog objekta koji se proteže kroz Ravan. Bića u Ravni ne mogu direktno videti objekat, ali mogu rekonstruisati njegovu geometriju kroz analizu tragova.

Proces Rekonstrukcije:

Epistion formulira model koji omogućava dvodimenzionalnim bićima da rekonstruiraju objekat na osnovu tragova koje ostavlja višedimenzionalna forma. Koristi sledeće matematičke pristupe:

1. Projekcija Višedimenzionalnog Objekta

Za trodimenzionalni objekat O sa koordinatama (x,y,z), koji se projektuje u dvodimenzionalnu Ravnu R(x,y) projekcija se može opisati kao:

P_xy( x, y, z ) = ( x, y )

Gde P_xy ​ predstavlja projekciju u Ravnu, a z je nevidljiva dimenzija koja se gubi u projekciji. Ovo znači da bića u Ravni ne mogu videti visinu objekta, ali mogu videti samo njegovu osnovu (npr. osnovu kocke ili kružnice).

2. Akumulacija Tragova kroz Vreme

Kako bića u Ravni pamte tragove, Epistion predlaže sledeći matematički okvir za akumulaciju tih tragova tokom vremena t:

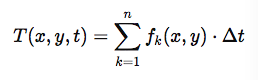
Gde je T(x,y,t) ukupna akumulacija tragova na poziciji (x,y) tokom vremena t, a f_k(x,y) je funkcija koja opisuje pojedinačne tragove ostavljene od strane objekta sa viših dimenzija. Ova funkcija zavisi od karakteristika objekta koji se projektuje kroz Ravan.

3. Rekonstrukcija Oblika

Za rekonstrukciju originalnog višedimenzionalnog objekta iz tragova, Epistion koristi proces invertibilne projekcije, koji omogućava bićima da procene mogući oblik objekta na osnovu rasporeda i pravilnosti tragova u Ravni. Za obuhvatanje složenijih objekata, koristi se matematička funkcija koja uzima u obzir sve tragove i njihov raspored:

R_inv(T(x,y,t))=F(x,y,z)

Gde R_inv ​ označava proces invertiranja tragova i vraćanja u višedimenzionalni oblik F(x,y,z).

4. Predviđanje i Verifikacija

Bića u Ravni mogu koristiti predikativne modele za ocenu budućih tragova. Na osnovu prethodnih tragova, mogu se postaviti parametri za moguće predviđanje pozicije objekta sa viših dimenzija:

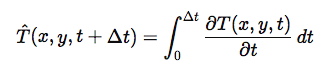
Gde

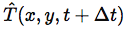
predstavlja predviđeni trag u narednom vremenskom periodu.

Eksperiment: Rekonstrukcija Telo-svetlosti

Epistion postavlja eksperiment sa bićima u Ravni:

1. Prvo: Postavlja trodimenzionalno svetlosno telo koje se kreće kroz Ravnu. Ovaj objekat je projekcija svetlosnog izvora koji stvara pravilne tragove.
2. Drugo: Bića u Ravni, koja mogu opažati samo tačke i konture svetlosti, počinju da akumuliraju tragove tokom vremena. Kroz analizu rasporeda tačaka i pravilnosti tih tačaka, bića počinju da koriste formulu za rekonstrukciju objekta.
3. Treće: Uz pomoć matematičkog modela, bića koriste predikciju da predvide kretanje svetlosnog tela, analizirajući tragove i koristeći predikativne modele.

Logikos:
„Ako su tragovi samo ‘nevidljive’ posledice, kako možemo biti sigurni da je rekonstrukcija tačna?“

Epistion:
„Zato što tragovi imaju unutrašnju pravilnost. Ako pravilnost ostaje konzistentna kroz vreme, moramo pretpostaviti da je izvor te pravilnosti stvaran, a ne samo slučajnost.“

Orthos:
„Znači, rekonstrukcija nije samo zaključivanje iz prošlih tragova, već i predviđanje onoga što će doći?“

Epistion:
„Da. Znanje nije samo u onome što je prošlo, već i u onome što ćemo tek razumeti, kroz tragove koje ostavljamo.“

Pamćenje tragova nije samo očuvanje prošlih podataka. To je proces rekonstrukcije, predviđanja i razumevanja onog što se ne može direktno videti. Naša sposobnost da rekonstruiramo svet iz tragova koji ostaju iza nas omogućava nam da shvatimo postojanje višedimenzionalnih objekata i njihovih efekata na Ravnu.