Kad račun iz prodavnice postane filozofija
Bio je običan dan, taman onako kako ih svi znamo — ništa neobično, bez najave nečeg što bi promenilo tok stvari. Otišao sam u lokalnu prodavnicu da kupim nešto za doručak: slaninu, kokakolu bez šećera i crni, rezani hleb. Obično stvari, ali kada sam došao na kasu, desilo se nešto neobično.
Kasirka je pogledala računar, otkucala cifre i tiho izgovorila:
— To je tačno 777 dinara.
Nasmejala se, a ja sam, privučen tom brojem, upitao:
— Šta znači baš ovaj broj?
Ona je samo odmahnula rukom i rekla:
— Ništa strašno. Neki brojevi su mnogo gori, ne brinite.
Ipak, ta rečenica ostavila me je sa neodgovorenim pitanjem. Šta su ti „gori“ brojevi? Zašto baš 777?
Vratio sam se kući, seo za računar i započeo svoje malo istraživanje. Tražio sam značenje tog broja — u filozofiji, religiji, kulturi, pa i u matematici. U filozofiji i religiji broj 777 je simbol savršenstva, duhovnog prosvetljenja, nečeg što prevazilazi naše svakodnevno shvatanje sveta. Ali u matematici? Tu nije bilo ničeg posebnog, samo običan broj.
Nije mi bilo dovoljno. Hteo sam da razumem zašto su ljudi kroz vekove baš tom broju pridavali toliki značaj. Šta je ta rezonanca, šta je veza između brojeva, prostora, svesti i strukture stvarnosti?
I tako je nastao moj prvi eksperiment: program pod imenom
Model rezonantne matrice 7×3: Transskalna dinamika kroz slojeve prostora, svesti i strukture.
U njemu sam pokušao da uhvatim te skrivene veze — kako se slojevi stvarnosti presijavaju kroz šablone brojeva, kako rezoniraju u nevidljivim dimenzijama između prostora i svesti. Možda je 777 više od običnog računa u prodavnici; možda je poziv na razumevanje, na istraživanje dubina koje se kriju iza svakodnevnog, na pronalaženje smisla u naizgled običnim stvarima.
I tako, taj dan u prodavnici, broj 777 nije bio samo cena, već početak nečeg mnogo većeg — ličnog istraživanja, filozofskog putovanja i stvaranja novog modela sveta kroz rezonancu brojeva.
Apstrakt
Predstavljen je matematički model koji opisuje interakciju između sedam rezonantnih slojeva u okviru tri komplementarna sveta: mikro (kvantni), mezo (ljudsko iskustvo) i makro (kosmički). Model koristi matricu stanja dimenzije 7×3 kako bi kvantifikovao frekventne ili energetske nivoe u svakoj dimenziji. Evolucija sistema definisana je diferencijalnim pravilima zasnovanim na rezonantnim principima i nelinearnim sopstvenim oscilacijama. Pojava koherentnog stanja (harmonijske sinhronizacije) interpretira se kao matematičko-ekvivalentna manifestacija broja 777. Model se primenjuje u teorijskim okvirima koji integrišu fiziku, psihologiju i kosmologiju, uz naglasak na transgeneracijsko nasleđe i fraktalnu povezanost kroz nivoe postojanja.
Model rezonantne matrice 7×3
1. Struktura modela
Model koristi matricu stanja \( R \) dimenzije 7×3, gde:
- Redovi \( i = 1..7 \) predstavljaju slojeve: materijalni, energijski, informacioni, psihološki, transgeneracijsko nasleđe, kolektivni, harmonijski
- Kolone \( j = 1..3 \) predstavljaju svetove: mikro, mezo, makro
Element \( r_{i,j} \in \mathbb{R} \) predstavlja rezonantnu vrednost sloja \( i \) u svetu \( j \).
2. Evolutivna dinamika
Promena vrednosti \( r_{i,j} \) u diskretnom vremenu je:
Gde su \( \alpha, \beta, \gamma \) koeficijenti, a \( N_{i,j} \) je nelinearni član (npr. \( \sin(r_{i,j}) \)).
3. Harmonijska funkcija
Harmonijska disperzija po svetu \( j \):
Ukupna harmonija sistema:
Koherentno stanje je kada je \( H(R) \approx 0 \).
4. Simbolika broja 777
Sistem se smatra harmonizovanim ako:
5. Transgeneracijsko nasleđe
Peti sloj modeluje prenos obrazaca u vremenu:
Gde su \( w_k \) težine prenosa informacija kroz generacije.
6. Numerička primena
Model se može implementirati kao dinamički sistem uz vizuelizaciju matrice \( R \), harmonijsku funkciju \( H(R) \) i spektralnu analizu svakog reda i kolone.
7. Zaključak
Model 7×3 povezuje kvantne, psihološke i kosmičke nivoe kroz rezonantnu dinamiku. Broj 777 predstavlja stanje visoke harmonije sistema. Ovaj pristup je pogodan za eksperimentalnu i simboličku interpretaciju svesti, prostora i vremena.
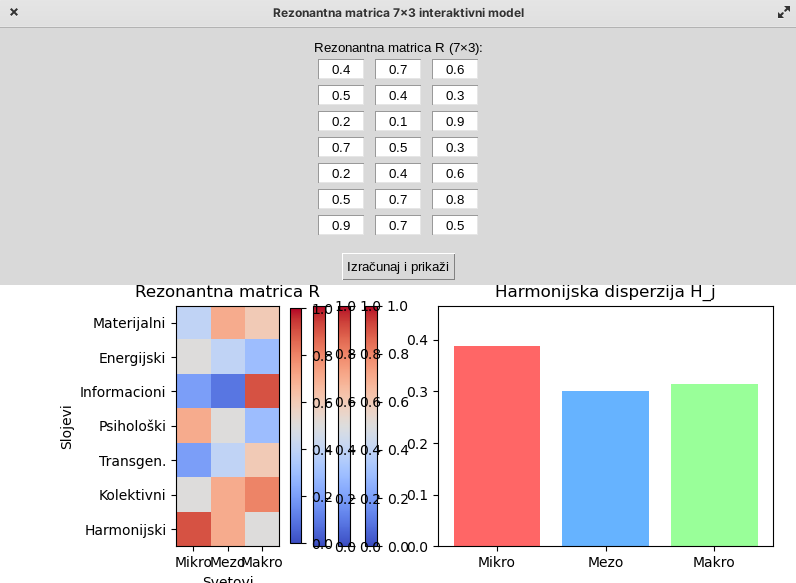
Programski kod za : rezonantna_matrica.py
#rezonantna_matrica.py
# Instalacija potrebnih zavisnosti: python3 -m pip install numpy matplotlib
import tkinter as tk
from tkinter import ttk
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
class ResonantMatrixApp:
def __init__(self, root):
self.root = root
self.root.title("Rezonantna matrica 7×3 interaktivni model")
self.layers = 7
self.worlds = 3
# Matrica vrednosti (inicijalno 0.5)
self.R = np.full((self.layers, self.worlds), 0.5)
# Tkinter frame za unose
self.entries = []
frame = ttk.Frame(root)
frame.pack(padx=10, pady=10)
ttk.Label(frame, text="Rezonantna matrica R (7×3):").grid(row=0, column=0, columnspan=self.worlds)
for i in range(self.layers):
row_entries = []
for j in range(self.worlds):
e = ttk.Entry(frame, width=6, justify='center')
e.grid(row=i+1, column=j, padx=3, pady=3)
e.insert(0, "0.5")
row_entries.append(e)
self.entries.append(row_entries)
# Dugme za osvežavanje
btn = ttk.Button(root, text="Izračunaj i prikaži", command=self.update_plot)
btn.pack(pady=5)
# Matplotlib figura u Tkinteru
self.fig, self.axs = plt.subplots(1, 2, figsize=(8, 3))
plt.tight_layout()
self.canvas = FigureCanvasTkAgg(self.fig, master=root)
self.canvas.get_tk_widget().pack()
self.update_plot()
def read_matrix(self):
for i in range(self.layers):
for j in range(self.worlds):
try:
val = float(self.entries[i][j].get())
if val < 0: val = 0
if val > 1: val = 1
except ValueError:
val = 0.5
self.R[i, j] = val
def harmonija(self):
H = []
for j in range(self.worlds):
mu = np.mean(self.R[:, j])
Hj = np.sum((self.R[:, j] - mu)**2)
H.append(Hj)
return np.array(H)
def update_plot(self):
self.read_matrix()
H = self.harmonija()
self.axs[0].clear()
self.axs[1].clear()
# Heatmap matrice R
im = self.axs[0].imshow(self.R, cmap='coolwarm', vmin=0, vmax=1)
self.axs[0].set_title('Rezonantna matrica R')
self.axs[0].set_xlabel('Svetovi')
self.axs[0].set_ylabel('Slojevi')
self.axs[0].set_xticks(range(self.worlds))
self.axs[0].set_xticklabels(['Mikro', 'Mezo', 'Makro'])
self.axs[0].set_yticks(range(self.layers))
self.axs[0].set_yticklabels(['Materijalni', 'Energijski', 'Informacioni', 'Psihološki',
'Transgen.', 'Kolektivni', 'Harmonijski'])
self.fig.colorbar(im, ax=self.axs[0], fraction=0.046, pad=0.04)
# Bar graf harmonije
self.axs[1].bar(['Mikro', 'Mezo', 'Makro'], H, color=['#ff6666', '#66b3ff', '#99ff99'])
self.axs[1].set_title('Harmonijska disperzija H_j')
self.axs[1].set_ylim(0, max(H)*1.2 if max(H)>0 else 1)
self.canvas.draw()
if __name__ == "__main__":
root = tk.Tk()
app = ResonantMatrixApp(root)
root.mainloop()