Eliptična kupola zasnovana na minimalnim površinama

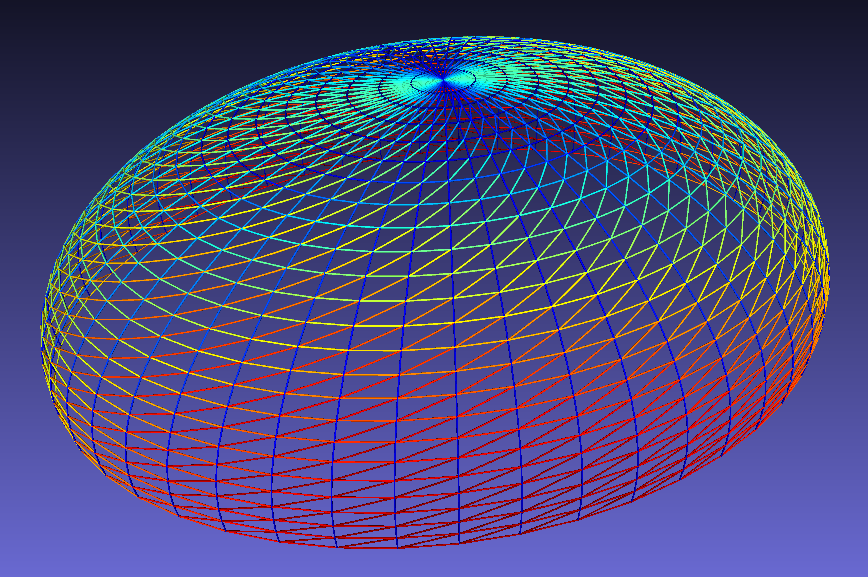
Geometrijski i matematički kontekst

Ova eliptična kupola nije klasična geodetska sfera niti segment sfere ili paraboloida. Umesto toga, zasniva se na minimalnoj površini — vrsti površine koja u svakoj tački minimizuje površinu pod uslovom da zadovoljava zadate ivice ili konture. To je ista matematika koja opisuje sapunske opne (soap films).

U ovom slučaju, konkretan oblik kupole je verovatno inspirisan Enneperovom površinom ili jednom od Schwarzovih P, D, H površina (poznatih minimalnih površina).

Minimalne površine se formalno definišu kao površine kod kojih je srednja zakrivljenost (mean curvature) jednaka nuli u svakoj tački:

Eliptična kupola je sofisticirana arhitektonska forma koja kombinuje estetsku privlačnost sa tehničkim i akustičkim prednostima. Koristi se u građevinama koje zahtevaju posebnu akustiku, jedinstven vizuelni doživljaj i često se sreće u sakralnoj i javnoj arhitekturi.

Eliptična kupola zasnovana na minimalnim površinama

📐 Geometrijski i matematički kontekst

Ova eliptična kupola nije klasična geodetska sfera niti segment sfere ili paraboloida. Umesto toga, zasniva se na minimalnoj površini – vrsti površine koja u svakoj tački minimizuje ukupnu površinu pod uslovom da zadovoljava određene konture. Takve površine se prirodno javljaju u fenomenu sapunskih opni.

U ovom slučaju, oblik kupole je inspirisan poznatim minimalnim površinama kao što su Enneperova površina i Schwarzove P, D i H površine. Njih karakteriše nulta srednja zakrivljenost:

H = (κ₁ + κ₂)/2 = 0

gde su κ₁ i κ₂ glavne zakrivljenosti u datoj tački površine.

🧠 Matematički model i numerička aproksimacija

Kupola se generiše numeričkim putem, najčešće diskretizacijom eliptične mreže i relaksacijom čvorova do forme koja zadovoljava minimalnu površinu. Primer parametrizacije Enneperove površine glasi:

x(u, v) = u - (u³)/3 + u·v²
y(u, v) = v - (v³)/3 + v·u²
z(u, v) = u² - v²

Za Schwarzove površine koristi se rešetkasta struktura u fundamentalnoj ćeliji, često generisana numerički. Program u Pythonu koristi sferoidne koordinate i optimizuje položaje tačaka tako da mreža šipki pokrije površinu nalik minimalnoj.

🏗️ Arhitektonska primena

Strukture inspirisane minimalnim površinama nalaze široku primenu u savremenoj arhitekturi zbog:

• optimalnog prenosa sila i stabilnosti konstrukcije,
• efikasne upotrebe materijala,
• estetskog i skulpturalnog izraza,
• lakog uklapanja u prirodna i urbane sredine.

Eliptične kupole ove vrste mogu se realizovati kao tensigrity sistemi, membranske konstrukcije, ili – kao u ovom slučaju – kao mrežne strukture od krutih šipki.

🔬 Tehničke metode proračuna

U numeričkom modeliranju ovakvih kupola koriste se metode kao što su:

• relaksacija opružnih mreža (spring relaxation),
• Laplaceovo izravnavanje čvorova,
• metode konačnih elemenata (FEM) za minimizaciju energije,
• diskretna Delaunay triangulacija na površini elipsoida.

Korišćenjem ovih metoda, kupola dobija stabilnu i optimizovanu formu sa izraženom geometrijskom harmonijom.

Ova konstrukcija je rezultat spoja matematičkog modelovanja i arhitektonske intuicije, predstavljajući savremen pristup oblikovanju prostora kroz forme koje priroda sama preferira.

PROGRAMSKI KOD

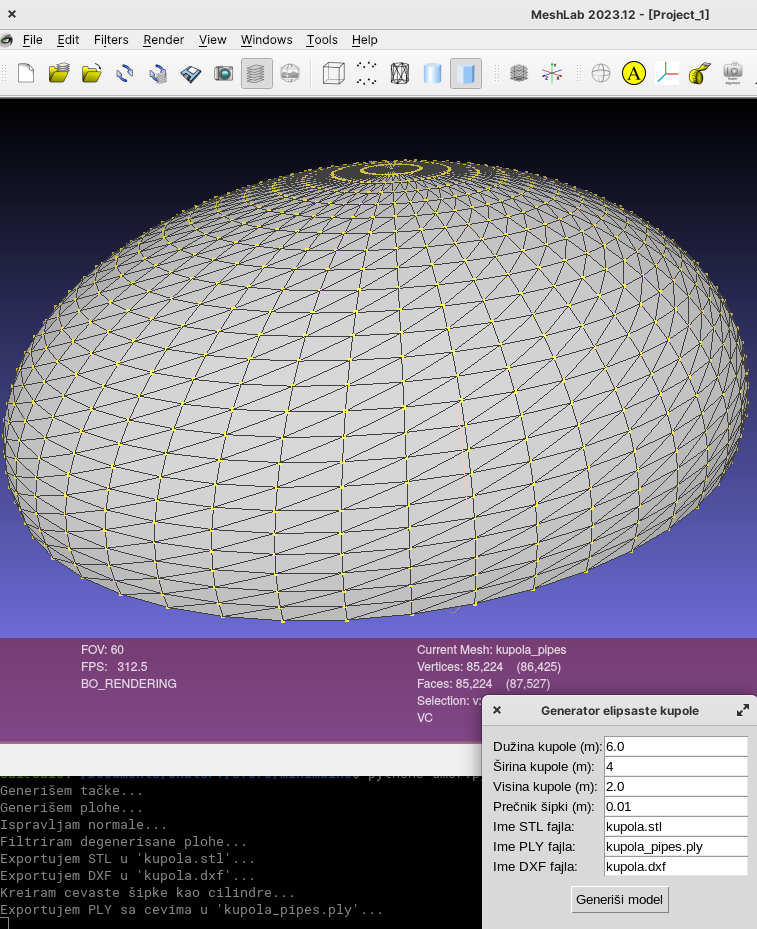
Instalacija potrebnih paketa

Otvorite terminal (Command Prompt, PowerShell, Terminal ili Anaconda Prompt) i ukucaj sledeću komandu:

pip install numpy meshio ezdxf matplotlib

Objašnjenje:

• numpy — za numeričke proračune.
• meshio — za čitanje i pisanje 3D mesh fajlova.
• ezdxf — za rad sa DXF fajlovima.
• matplotlib — za colormap (cm) i druge grafičke funkcije.

Programski kod za eliptkup.py

import numpy as np
import meshio
import ezdxf
import tkinter as tk
from tkinter import ttk, messagebox
from math import pi, cos, sin
from matplotlib import cm  # ispravan uvoz cmap

def generate_ellipsoid_grid(a, b, c, u_steps=50, v_steps=25):
    u = np.linspace(0, 2 * pi, u_steps)
    v = np.linspace(0, pi / 2, v_steps)
    points = []
    for vi in v:
        for ui in u:
            x = a * cos(ui) * sin(vi)
            y = b * sin(ui) * sin(vi)
            z = c * cos(vi)
            points.append([x, y, z])
    points = np.array(points)
    return points, u_steps, v_steps

def generate_faces(u_steps, v_steps):
    faces = []
    for i in range(v_steps - 1):
        for j in range(u_steps - 1):
            p0 = i * u_steps + j
            p1 = p0 + 1
            p2 = p0 + u_steps
            p3 = p2 + 1
            # dva trougla
            faces.append([p0, p2, p1])
            faces.append([p1, p2, p3])
        # Zatvaranje prstena oko u
        p0 = i * u_steps + (u_steps - 1)
        p1 = i * u_steps
        p2 = p0 + u_steps
        p3 = p1 + u_steps
        faces.append([p0, p2, p1])
        faces.append([p1, p2, p3])
    return np.array(faces)

def correct_normals(points, faces):
    center = np.array([0,0,0])
    new_faces = []
    for f in faces:
        v0, v1, v2 = points[f[0]], points[f[1]], points[f[2]]
        normal = np.cross(v1 - v0, v2 - v0)
        centroid = (v0 + v1 + v2) / 3
        if np.dot(normal, centroid - center) < 0:
            new_faces.append([f[0], f[2], f[1]])
        else:
            new_faces.append([f[0], f[1], f[2]])
    return np.array(new_faces)

def filter_degenerate_faces(points, faces, tol=1e-8):
    filtered = []
    for f in faces:
        v0, v1, v2 = points[f[0]], points[f[1]], points[f[2]]
        area = np.linalg.norm(np.cross(v1 - v0, v2 - v0)) / 2
        if area > tol:
            filtered.append(f)
    return np.array(filtered)

def export_stl(filename, points, faces):
    cells = [("triangle", faces.astype(np.int32))]
    meshio.write_points_cells(filename, points.astype(np.float32), cells)

def export_dxf(filename, points, faces):
    doc = ezdxf.new(dxfversion='R2010')
    msp = doc.modelspace()
    for f in faces:
        v0, v1, v2 = points[f[0]], points[f[1]], points[f[2]]
        msp.add_3dface([v0.tolist(), v1.tolist(), v2.tolist()])
    doc.saveas(filename)

def generate_cylinder_mesh(p0, p1, radius, segments=12):
    axis = p1 - p0
    length = np.linalg.norm(axis)
    if length < 1e-12:
        return np.array([]), np.array([])

    axis = axis / length

    if abs(axis[0]) < 1e-6 and abs(axis[1]) < 1e-6:
        tangent = np.array([1,0,0])
    else:
        tangent = np.array([-axis[1], axis[0], 0])
    tangent /= np.linalg.norm(tangent)

    bitangent = np.cross(axis, tangent)

    angle_step = 2 * pi / segments
    circle_points_start = []
    circle_points_end = []
    for i in range(segments):
        angle = i * angle_step
        offset = radius * (cos(angle) * tangent + sin(angle) * bitangent)
        circle_points_start.append(p0 + offset)
        circle_points_end.append(p1 + offset)

    vertices = np.array(circle_points_start + circle_points_end)

    faces = []
    for i in range(segments):
        i_next = (i + 1) % segments
        faces.append([i, i_next, segments + i])
        faces.append([segments + i, i_next, segments + i_next])
    return vertices, np.array(faces)

def create_pipes_mesh(points, faces, radius, segments=12):
    edges_set = set()
    for tri in faces:
        for i in range(3):
            a, b = sorted((tri[i], tri[(i+1)%3]))
            edges_set.add((a,b))
    edges = list(edges_set)

    # Grupisanje ivica po dužini
    lengths = np.array([np.linalg.norm(points[e[0]] - points[e[1]]) for e in edges])
    unique_lengths = np.unique(np.round(lengths, decimals=5))  # za grupisanje sa malom tolerancijom

    # Karta od dužine do boje
    cmap = cm.get_cmap('jet', len(unique_lengths))
    length_to_color = {}
    for i, ul in enumerate(unique_lengths):
        length_to_color[ul] = cmap(i)[:3]  # rgb float 0-1

    all_vertices = []
    all_faces = []
    all_colors = []
    vertex_offset = 0

    for edge, length in zip(edges, lengths):
        p0, p1 = points[edge[0]], points[edge[1]]
        cyl_verts, cyl_faces = generate_cylinder_mesh(p0, p1, radius, segments)
        if cyl_verts.size == 0:
            continue

        all_vertices.append(cyl_verts)
        all_faces.append(cyl_faces + vertex_offset)

        # Dodeli boju na osnovu dužine (nalazi najbližu jedinstvenu dužinu)
        length_key = unique_lengths[np.abs(unique_lengths - round(length,5)).argmin()]
        rgb = length_to_color[length_key]
        # Pretvori u 0-255 uint8
        color = np.array(rgb) * 255
        color = color.astype(np.uint8)

        # Svaki vertex cilindra ima istu boju
        all_colors.append(np.tile(color, (len(cyl_verts),1)))

        vertex_offset += len(cyl_verts)

    if len(all_vertices) == 0:
        return np.array([]), np.array([]), np.array([])

    all_vertices = np.vstack(all_vertices)
    all_faces = np.vstack(all_faces)
    all_colors = np.vstack(all_colors)

    return all_vertices, all_faces, all_colors

def export_ply(filename, vertices, faces, colors):
    if vertices.size == 0 or faces.size == 0:
        raise ValueError("Nema podataka za eksport PLY")

    point_data = {
        "red": colors[:, 0],
        "green": colors[:, 1],
        "blue": colors[:, 2]
    }

    cells = [("triangle", faces.astype(np.int32))]
    meshio.write_points_cells(
        filename,
        vertices.astype(np.float32),
        cells,
        point_data=point_data
    )

def on_generate():
    try:
        length = float(entry_length.get())
        width = float(entry_width.get())
        height = float(entry_height.get())
        pipe_diameter = float(entry_diameter.get())
        stl_file = entry_stl.get()
        ply_file = entry_ply.get()
        dxf_file = entry_dxf.get()

        a = length / 2
        b = width / 2
        c = height

        print("Generišem tačke...")
        points, u_steps, v_steps = generate_ellipsoid_grid(a, b, c)

        print("Generišem plohe...")
        faces = generate_faces(u_steps, v_steps)

        print("Ispravljam normale...")
        faces = correct_normals(points, faces)

        print("Filtriram degenerisane plohe...")
        faces = filter_degenerate_faces(points, faces)

        print(f"Exportujem STL u '{stl_file}'...")
        export_stl(stl_file, points, faces)

        print(f"Exportujem DXF u '{dxf_file}'...")
        export_dxf(dxf_file, points, faces)

        print("Kreiram cevaste šipke kao cilindre...")
        pipe_radius = pipe_diameter / 2
        pipe_verts, pipe_faces, pipe_colors = create_pipes_mesh(points, faces, pipe_radius, segments=12)

        print(f"Exportujem PLY sa cevima u '{ply_file}'...")
        export_ply(ply_file, pipe_verts, pipe_faces, pipe_colors)

        messagebox.showinfo("Gotovo", "Model je uspešno generisan i sačuvan!")
    except Exception as e:
        messagebox.showerror("Greška", str(e))

root = tk.Tk()
root.title("Generator elipsaste kupole")

frame = ttk.Frame(root, padding=10)
frame.grid(row=0, column=0)

ttk.Label(frame, text="Dužina kupole (m):").grid(row=0, column=0, sticky="w")
entry_length = ttk.Entry(frame)
entry_length.insert(0, "6.0")
entry_length.grid(row=0, column=1)

ttk.Label(frame, text="Širina kupole (m):").grid(row=1, column=0, sticky="w")
entry_width = ttk.Entry(frame)
entry_width.insert(0, "4.5")
entry_width.grid(row=1, column=1)

ttk.Label(frame, text="Visina kupole (m):").grid(row=2, column=0, sticky="w")
entry_height = ttk.Entry(frame)
entry_height.insert(0, "3.0")
entry_height.grid(row=2, column=1)

ttk.Label(frame, text="Prečnik šipki (m):").grid(row=3, column=0, sticky="w")
entry_diameter = ttk.Entry(frame)
entry_diameter.insert(0, "0.04")
entry_diameter.grid(row=3, column=1)

ttk.Label(frame, text="Ime STL fajla:").grid(row=4, column=0, sticky="w")
entry_stl = ttk.Entry(frame)
entry_stl.insert(0, "kupola.stl")
entry_stl.grid(row=4, column=1)

ttk.Label(frame, text="Ime PLY fajla:").grid(row=5, column=0, sticky="w")
entry_ply = ttk.Entry(frame)
entry_ply.insert(0, "kupola_pipes.ply")
entry_ply.grid(row=5, column=1)

ttk.Label(frame, text="Ime DXF fajla:").grid(row=6, column=0, sticky="w")
entry_dxf = ttk.Entry(frame)
entry_dxf.insert(0, "kupola.dxf")
entry_dxf.grid(row=6, column=1)

btn_generate = ttk.Button(frame, text="Generiši model", command=on_generate)
btn_generate.grid(row=7, column=0, columnspan=2, pady=10)

root.mainloop()