https://abel.rs/as/geodetska_kupola.html

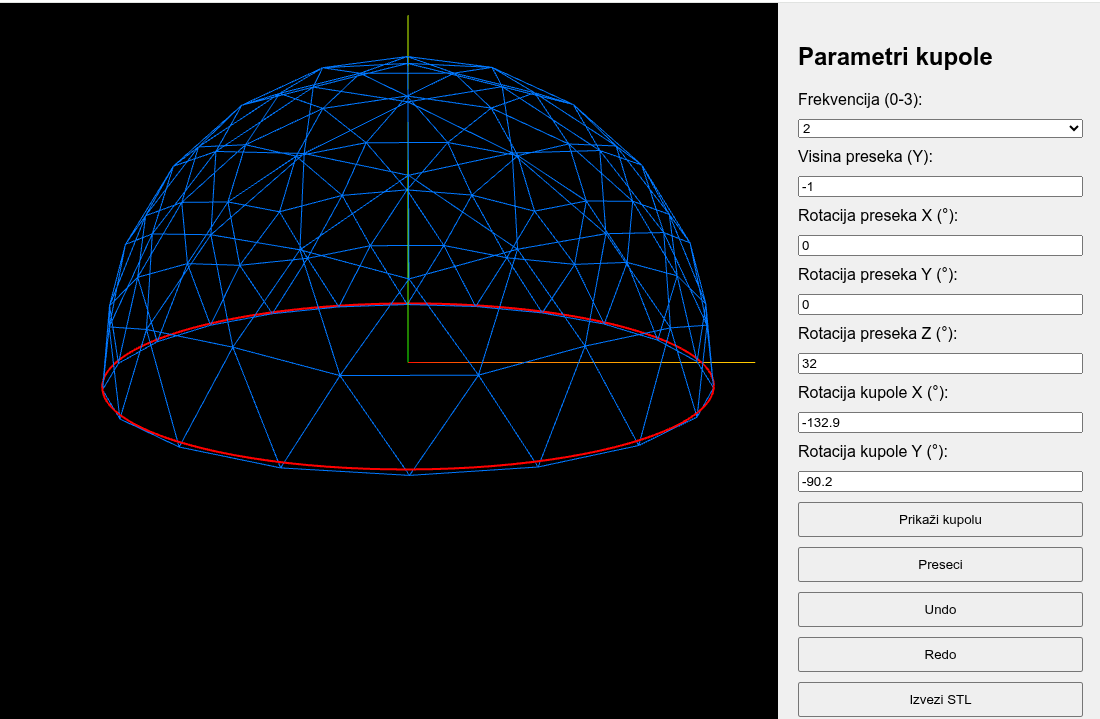
Predstavljamo napredni web program koji omogućava korisnicima da lako i intuitivno kreiraju, prilagođavaju i izvoze 3D modele geodetskih kupola. Ovaj alat kombinuje modernu tehnologiju web preglednika i moćne biblioteke Three.js, pružajući bogat skup funkcionalnosti za arhitekte, dizajnere, inženjere i entuzijaste.

Glavne funkcionalnosti programa:

1. Generisanje geodetske kupole sa podesivom frekvencijom

Program korisniku nudi izbor frekvencije kupole od 0 do 3, gde:

• Frekvencija 0 predstavlja osnovni ikosaedar.
• Veće frekvencije (1, 2, 3) donose detaljnije i finije mreže koje približavaju kupolu sfernom obliku.

Na osnovu odabrane frekvencije, algoritam generiše geometriju kupole koristeći principe geometrije i normalizacije vrhova na sferu. Rezultat je precizan i vizuelno atraktivan 3D model koji se prikazuje u realnom vremenu.

2. Interaktivno sečenje kupole po visini i rotaciji preseka

Jedna od posebnih karakteristika programa je mogućnost presecanja kupole duž visine (Y ose) sa dodatnim podešavanjima rotacije preseka oko X, Y i Z osa. Ovo omogućava korisniku da:

• Izreže gornji deo kupole, dobijajući polu-kupolu ili drugačije geometrijske oblike.
• Precizno pozicionira i orijentiše preseke radi optimizacije oblika ili pripreme za dalje modifikacije i izradu.

3. Rotacija cele kupole

Pored preseka, program nudi i kontrolu rotacije cele kupole oko X i Y osa. Ova funkcionalnost je izuzetno korisna za pregled i analizu modela iz različitih uglova, kao i za pripremu za izvoz i dalju upotrebu.

4. Undo/Redo funkcije za upravljanje promenama

Korisničko iskustvo je značajno unapređeno zahvaljujući undo i redo funkcijama koje omogućavaju:

• Vraćanje na prethodna stanja modela nakon presecanja ili drugih izmena.
• Ponovno vraćanje promena ako se želi testirati različite varijante bez straha od gubitka rada.

Ove funkcije čine rad s programom fleksibilnim i sigurnim.

5. Vizuelizacija u realnom vremenu koristeći Three.js

Program koristi Three.js, jednu od najpopularnijih JavaScript biblioteka za 3D grafiku u webu, što omogućava:

• Kvalitetnu grafiku i glatku animaciju modela u realnom vremenu.
• Dinamičko osvetljenje i senke koje poboljšavaju vizuelni doživljaj.
• Prilagodljiv prikaz koji se automatski skalira prilikom promene veličine prozora.

6. Izvoz modela u STL format za 3D štampu i dalju obradu

U planu je da se program doradi tako da korisnik nakon što kreira i prilagodi svoju kupolu, može da je lako izveze u popularni STL format:

• STL fajl je široko podržan u softverima za 3D štampu i CAD aplikacijama.
• Omogućava direktnu proizvodnju modela ili dodatnu obradu u specijalizovanim alatima.

Ovaj program predstavlja moćan i pristupačan alat za sve koji žele da se bave geodetskim kupolama, bilo u edukaciji, arhitekturi, ili inženjeringu. Intuitivni interfejs, bogat skup funkcija i mogućnost izvoza modela čine ga idealnim izborom za brzo kreiranje, prilagođavanje i deljenje 3D kupola.

Isprobajte ga i otkrijte kako tehnologija može pojednostaviti i unaprediti vaše kreativne projekte!

Matematika geodetske kupole u programu

Ovaj dokument detaljno objašnjava matematičke principe korišćene u programu za generisanje geodetskih kupola. Cilj je da razumemo kako se iz osnovnog ikosaedra dobijaju složenije i preciznije strukture pomoću geometrijskih transformacija i subdivizije.

1. Osnovni poliedar: Ikosaedar

Geodetska kupola počinje od regularnog ikosaedra, koji ima:

• 12 temena (vrhova)
• 20 trouglastih lica
• 30 ivica

Koordinate temena ikosaedra koriste se kao polazne tačke za konstrukciju kupole.

Koordinate temena ikosaedra

Ako je \( t = \frac{1 + \sqrt{5}}{2} \) (zlatni rez), tada su vrhovi definisani kao:

[
  (-1,  t,  0), ( 1,  t,  0), (-1, -t,  0), ( 1, -t,  0),
  ( 0, -1,  t), ( 0,  1,  t), ( 0, -1, -t), ( 0,  1, -t),
  ( t,  0, -1), ( t,  0,  1), (-t,  0, -1), (-t,  0,  1)
]
  

Ove koordinate se zatim normalizuju na poluprečnik sfere (npr. 100 jedinica) da bi temena ležala na sferi.

2. Normalizacija vrhova na sferu

Svaki vektor temena se normalizuje (pretvara u jedinični vektor) i zatim se skaluje na željeni poluprečnik \( R \).

\[ \mathbf{v}_{norm} = R \times \frac{\mathbf{v}}{|\mathbf{v}|} \]

Gde je:

• \(\mathbf{v} = (x, y, z)\) originalni vektor
• \(|\mathbf{v}| = \sqrt{x^2 + y^2 + z^2}\) norma (dužina) vektora
• \(R\) željeni poluprečnik sfere

3. Subdivizija trouglova

Svako trouglasto lice ikosaedra se deli na manje trouglove radi dobijanja glatkije i detaljnije površine kupole.

Proces subdivizije sa dubinom \( d \) radi se rekuzivno:

• Za svaki trougao sa temenima \(\mathbf{v_1}, \mathbf{v_2}, \mathbf{v_3}\), računa se sredina svake ivice:

  \[ \mathbf{v_{12}} = \frac{\mathbf{v_1} + \mathbf{v_2}}{2}, \quad \mathbf{v_{23}} = \frac{\mathbf{v_2} + \mathbf{v_3}}{2}, \quad \mathbf{v_{31}} = \frac{\mathbf{v_3} + \mathbf{v_1}}{2} \]

• Svaka sredina se normalizuje na poluprečnik sfere kao u prethodnom koraku.
• Originalni trougao se zamenjuje sa četiri nova trougla: \[ (\mathbf{v_1}, \mathbf{v_{12}}, \mathbf{v_{31}}), \quad (\mathbf{v_2}, \mathbf{v_{23}}, \mathbf{v_{12}}), \quad (\mathbf{v_3}, \mathbf{v_{31}}, \mathbf{v_{23}}), \quad (\mathbf{v_{12}}, \mathbf{v_{23}}, \mathbf{v_{31}}) \]
• Ovaj proces se ponavlja dok se ne dostigne željena dubina subdivizije, koja je u programu definisana kao frekvencija kupole.

4. Frekvencija kupole

Frekvencija (\( freq \)) određuje koliko puta se svaki trougao ikosaedra deli. Veća frekvencija znači:

• Više manjih trouglova
• Finoću i bolju aproksimaciju sfere

Na primer:

• \( freq = 0 \): osnovni ikosaedar (20 trouglova)
• \( freq = 1 \): svaki trougao podeljen na 4
• \( freq = 2 \): svaki trougao podeljen na 16 \((4^2)\)
• \( freq = 3 \): svaki trougao podeljen na 64 \((4^3)\)

5. Presecanje kupole

Nakon generisanja kupole, moguće je preseći je na određenoj visini \( h \) duž Y ose. Program uklanja sve trouglove koji imaju sva tri temena ispod te visine.

Matematika preseka je jednostavna:

• Za svaki trougao proveriti Y koordinate temena \( y_1, y_2, y_3 \)
• Ako su \( y_1, y_2, y_3 \geq h \), trougao se zadržava
• Inače, trougao se odbacuje

6. Rotacije modela

Rotacije se primenjuju na ceo model ili na preseke, rotiranjem oko X, Y ili Z ose pomoću rotacionih matrica.

Matrica rotacije oko X ose za ugao \( \theta \): \[ R_x(\theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix} \]

Matrica rotacije oko Y ose za ugao \( \phi \): \[ R_y(\phi) = \begin{bmatrix} \cos\phi & 0 & \sin\phi \\ 0 & 1 & 0 \\ -\sin\phi & 0 & \cos\phi \end{bmatrix} \]

Matrica rotacije oko Z ose za ugao \( \psi \): \[ R_z(\psi) = \begin{bmatrix} \cos\psi & -\sin\psi & 0 \\ \sin\psi & \cos\psi & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

Svaka tačka \( \mathbf{p} = (x, y, z) \) rotira se množenjem sa odgovarajućom rotacionom matricom.

Zaključak

Program koristi elegantnu kombinaciju geometrijskih transformacija, poliedarskih osnovnih oblika i matematičke logike da bi generisao i manipulirao kompleksnim 3D modelima geodetskih kupola. Razumevanje ovih principa pomaže u prilagođavanju i daljem razvoju softvera.

Autor: Abel | Datum: 2025

Programski kod za geodetska_kupola.html:

<!DOCTYPE html>
<html lang="en">
<head>
  <meta charset="UTF-8" />
  <title>Geodetska Kupola</title>
  <style>
    body, html { margin: 0; height: 100%; overflow: hidden; font-family: sans-serif; }
    #container { display: flex; height: 100vh; }
    #renderer { flex: 1; background: #e0e0e0; }
    #controls {
      position: absolute;
      right: 0; top: 0; bottom: 0;
      width: 300px;
      padding: 20px;
      background: #f0f0f0;
      box-shadow: -2px 0 5px rgba(0,0,0,0.1);
      overflow-y: auto;
      z-index: 10;
    }
    label, select, input, button {
      display: block;
      margin-bottom: 10px;
      width: 100%;
      box-sizing: border-box;
    }
    button {
      cursor: pointer;
      padding: 8px;
    }
  </style>
</head>
<body>
  <div id="container">
    <div id="renderer"></div>
    <div id="controls">
      <h2>Parametri kupole</h2>
      <label for="frequency">Frekvencija (0-3):</label>
      <select id="frequency">
        <option value="0">0 (Ikosaedar)</option>
        <option value="1">1</option>
        <option value="2">2</option>
        <option value="3">3</option>
      </select>

      <label for="sliceHeight">Visina preseka (Y):</label>
      <input type="number" id="sliceHeight" value="0" step="1" />

      <label for="sliceRotX">Rotacija preseka X (°):</label>
      <input type="number" id="sliceRotX" value="0" step="0.1" />
      <label for="sliceRotY">Rotacija preseka Y (°):</label>
      <input type="number" id="sliceRotY" value="0" step="0.1" />
      <label for="sliceRotZ">Rotacija preseka Z (°):</label>
      <input type="number" id="sliceRotZ" value="0" step="0.1" />

      <label for="rotX">Rotacija kupole X (°):</label>
      <input type="number" id="rotX" value="0" step="0.1" />
      <label for="rotY">Rotacija kupole Y (°):</label>
      <input type="number" id="rotY" value="0" step="0.1" />

      <button id="showBtn">Prikaži kupolu</button>
      <button id="sliceBtn">Preseci</button>
      <button id="undoBtn">Undo</button>
      <button id="redoBtn">Redo</button>
      <button id="exportBtn">Izvezi STL</button>
    </div>
  </div>

<script src="https://cdn.jsdelivr.net/npm/three@0.153.0/build/three.min.js"></script>
<script src="https://cdn.jsdelivr.net/npm/three@0.153.0/examples/js/exporters/STLExporter.js"></script>
<script>
const DISPLAY_RADIUS = 100;

const scene = new THREE.Scene();
const camera = new THREE.PerspectiveCamera(45, (window.innerWidth - 300) / window.innerHeight, 0.1, 1000);
camera.position.set(0, 0, 300);

const renderer = new THREE.WebGLRenderer({ antialias: true });
renderer.setSize(window.innerWidth - 300, window.innerHeight);
document.getElementById('renderer').appendChild(renderer.domElement);

const ambient = new THREE.AmbientLight(0xffffff, 0.8);
const directional = new THREE.DirectionalLight(0xffffff, 0.6);
directional.position.set(1, 1, 1);
scene.add(ambient, directional);

const domeGroup = new THREE.Group();
scene.add(domeGroup);

// Axes helper to show coordinate system at center
const axesHelper = new THREE.AxesHelper(120);
scene.add(axesHelper);

let isDragging = false;
let prevMouse = {x: 0, y: 0};
let rotation = {x: 0, y: 0};
let rotationXInput = document.getElementById('rotX');
let rotationYInput = document.getElementById('rotY');

renderer.domElement.addEventListener('mousedown', e => {
  isDragging = true;
  prevMouse = {x: e.clientX, y: e.clientY};
});
renderer.domElement.addEventListener('mouseup', e => {
  isDragging = false;
});
renderer.domElement.addEventListener('mousemove', e => {
  if (!isDragging) return;
  const dx = e.clientX - prevMouse.x;
  const dy = e.clientY - prevMouse.y;
  rotation.y += dx * 0.005;
  rotation.x += dy * 0.005;
  prevMouse = {x: e.clientX, y: e.clientY};
  updateRotationInputs();
});

rotationXInput.addEventListener('input', e => {
  let val = parseFloat(rotationXInput.value);
  if (!isNaN(val)) {
    rotation.x = THREE.MathUtils.degToRad(val);
  }
});
rotationYInput.addEventListener('input', e => {
  let val = parseFloat(rotationYInput.value);
  if (!isNaN(val)) {
    rotation.y = THREE.MathUtils.degToRad(val);
  }
});

function updateRotationInputs(){
  rotationXInput.value = THREE.MathUtils.radToDeg(rotation.x).toFixed(1);
  rotationYInput.value = THREE.MathUtils.radToDeg(rotation.y).toFixed(1);
}

// Icosahedron base vertices and faces
const t = (1 + Math.sqrt(5)) / 2;
const icoVertices = [
  [-1,  t,  0], [1,  t,  0], [-1, -t,  0], [1, -t,  0],
  [0, -1,  t], [0,  1,  t], [0, -1, -t], [0,  1, -t],
  [ t,  0, -1], [ t,  0,  1], [-t,  0, -1], [-t,  0,  1]
].map(v => new THREE.Vector3(...v));

const icoFaces = [
  [0, 11, 5], [0, 5, 1], [0, 1, 7], [0, 7, 10], [0, 10, 11],
  [1, 5, 9], [5, 11, 4], [11, 10, 2], [10, 7, 6], [7, 1, 8],
  [3, 9, 4], [3, 4, 2], [3, 2, 6], [3, 6, 8], [3, 8, 9],
  [4, 9, 5], [2, 4, 11], [6, 2, 10], [8, 6, 7], [9, 8, 1]
];

function normalizeAndScale(v, r) {
  return v.clone().normalize().multiplyScalar(r);
}

function subdivideTriangle(v1, v2, v3, depth) {
  if (depth === 0) return [[v1, v2, v3]];
  let v12 = normalizeAndScale(v1.clone().add(v2).multiplyScalar(0.5), DISPLAY_RADIUS);
  let v23 = normalizeAndScale(v2.clone().add(v3).multiplyScalar(0.5), DISPLAY_RADIUS);
  let v31 = normalizeAndScale(v3.clone().add(v1).multiplyScalar(0.5), DISPLAY_RADIUS);
  return [
    ...subdivideTriangle(v1, v12, v31, depth - 1),
    ...subdivideTriangle(v2, v23, v12, depth - 1),
    ...subdivideTriangle(v3, v31, v23, depth - 1),
    ...subdivideTriangle(v12, v23, v31, depth - 1)
  ];
}

let currentTris = [];
let currentFreq = 0;

function createDome(freq) {
  domeGroup.clear();
  currentFreq = freq;
  currentTris = [];
  for (let face of icoFaces) {
    const [i1, i2, i3] = face;
    const v1 = normalizeAndScale(icoVertices[i1], DISPLAY_RADIUS);
    const v2 = normalizeAndScale(icoVertices[i2], DISPLAY_RADIUS);
    const v3 = normalizeAndScale(icoVertices[i3], DISPLAY_RADIUS);
    currentTris.push(...subdivideTriangle(v1, v2, v3, freq));
  }
  drawDomeLines(currentTris);
}

function drawDomeLines(tris) {
  domeGroup.clear();
  const mat = new THREE.LineBasicMaterial({ color: 0x0077ff });
  for (let tri of tris) {
    const geo = new THREE.BufferGeometry().setFromPoints([...tri, tri[0]]);
    const line = new THREE.Line(geo, mat);
    domeGroup.add(line);
  }
  addSliceLine();
}

// Undo/Redo stacks
const undoStack = [];
const redoStack = [];

function pushState() {
  undoStack.push({
    tris: currentTris.map(tri => tri.map(v => v.clone())),
    freq: currentFreq,
    rotationX: rotation.x,
    rotationY: rotation.y,
    sliceHeight: parseFloat(sliceHeightInput.value),
    sliceRotX: parseFloat(sliceRotXInput.value),
    sliceRotY: parseFloat(sliceRotYInput.value),
    sliceRotZ: parseFloat(sliceRotZInput.value)
  });
  if (undoStack.length > 50) undoStack.shift();
}

function popState() {
  if (undoStack.length === 0) return null;
  return undoStack.pop();
}

function pushRedoState(state) {
  redoStack.push(state);
  if (redoStack.length > 50) redoStack.shift();
}

function popRedoState() {
  if (redoStack.length === 0) return null;
  return redoStack.pop();
}

function restoreState(state) {
  if (!state) return;
  currentTris = state.tris.map(tri => tri.map(v => v.clone()));
  currentFreq = state.freq;
  rotation.x = state.rotationX;
  rotation.y = state.rotationY;
  sliceHeightInput.value = state.sliceHeight;
  sliceRotXInput.value = state.sliceRotX;
  sliceRotYInput.value = state.sliceRotY;
  sliceRotZInput.value = state.sliceRotZ;
  updateRotationInputs();
  drawDomeLines(currentTris);
  applyRotationToDome();
  updateSlicePlane();
}

function clearRedoStack() {
  redoStack.length = 0;
}

// Slice plane and helpers
const sliceHeightInput = document.getElementById('sliceHeight');
const sliceRotXInput = document.getElementById('sliceRotX');
const sliceRotYInput = document.getElementById('sliceRotY');
const sliceRotZInput = document.getElementById('sliceRotZ');

const sliceLineMaterial = new THREE.LineBasicMaterial({ color: 0xff0000, linewidth: 2 });
let sliceLine = null;

// Slice plane is a THREE.Plane with rotation and height controls
const slicePlane = new THREE.Plane(new THREE.Vector3(0, 1, 0), 0);

function addSliceLine() {
  if (sliceLine) {
    domeGroup.remove(sliceLine);
  }
  // Compute a large line along intersection with sphere, approximated by circle intersection with plane
  // We'll draw a red circle on sphere showing intersection
  const points = [];
  const segments = 128;
  const radius = DISPLAY_RADIUS;
  // slicePlane is defined by normal and constant d: normal.dot(point) + d = 0
  // We'll sample points on a circle on sphere intersected by the plane:
  // We find two orthogonal vectors in plane:
  let normal = slicePlane.normal.clone();
  let u = new THREE.Vector3();
  if (Math.abs(normal.x) > 0.1 || Math.abs(normal.z) > 0.1) {
    u.set(-normal.z, 0, normal.x).normalize();
  } else {
    u.set(1, 0, 0);
  }
  let v = new THREE.Vector3().crossVectors(normal, u);
  for(let i=0; i<=segments; i++){
    let angle = (i/segments)*Math.PI*2;
    // point on plane circle:
    let p = new THREE.Vector3().addScaledVector(u, Math.cos(angle)*radius)
                               .addScaledVector(v, Math.sin(angle)*radius);
    // project onto plane:
    let distToPlane = normal.dot(p) + slicePlane.constant;
    p.addScaledVector(normal, -distToPlane);
    // normalize to radius to lie on sphere surface:
    p.normalize().multiplyScalar(radius);
    points.push(p);
  }
  const geo = new THREE.BufferGeometry().setFromPoints(points);
  sliceLine = new THREE.LineLoop(geo, sliceLineMaterial);
  domeGroup.add(sliceLine);
}

// Update slicePlane from inputs
function updateSlicePlane(){
  // Rotation inputs are in degrees
  let rx = THREE.MathUtils.degToRad(parseFloat(sliceRotXInput.value) || 0);
  let ry = THREE.MathUtils.degToRad(parseFloat(sliceRotYInput.value) || 0);
  let rz = THREE.MathUtils.degToRad(parseFloat(sliceRotZInput.value) || 0);

  // Start normal vector (0,1,0)
  let normal = new THREE.Vector3(0,1,0);
  // Apply rotations (order ZYX)
  let euler = new THREE.Euler(rx, ry, rz, 'ZYX');
  normal.applyEuler(euler).normalize();

  // Distance from origin (negative sliceHeight to match THREE.Plane sign convention)
  let d = -parseFloat(sliceHeightInput.value) || 0;

  slicePlane.set(normal, d);

  // Redraw line
  addSliceLine();
}

// Apply rotation from inputs to domeGroup
function applyRotationToDome() {
  domeGroup.rotation.x = rotation.x;
  domeGroup.rotation.y = rotation.y;
}

function sliceDome() {
  // Slice dome: remove all triangles with all 3 points below the slice plane (plane normal.dot(point)+constant > 0 is above)
  let normal = slicePlane.normal;
  let constant = slicePlane.constant;

  const filteredTris = currentTris.filter(tri => {
    // If at least one vertex is above or on the plane (normal.dot(v)+d <=0), keep
    for (let v of tri) {
      if (normal.dot(v) + constant <= 0) return true;
    }
    return false;
  });
  currentTris = filteredTris;
  drawDomeLines(currentTris);
  applyRotationToDome();
}

function exportSTL() {
  const exporter = new THREE.STLExporter();
  // Build geometry from current triangles:
  let geometry = new THREE.BufferGeometry();
  let positions = [];
  for(let tri of currentTris) {
    tri.forEach(v => {
      positions.push(v.x, v.y, v.z);
    });
  }
  geometry.setAttribute('position', new THREE.Float32BufferAttribute(positions, 3));
  geometry.setIndex([...Array(currentTris.length).keys()].flatMap(i => [i*3, i*3+1, i*3+2]));
  // Create mesh for export
  let material = new THREE.MeshStandardMaterial();
  let mesh = new THREE.Mesh(geometry, material);
  mesh.rotation.x = rotation.x;
  mesh.rotation.y = rotation.y;
  const stlString = exporter.parse(mesh);
  const freq = document.getElementById('frequency').value;
  const rx = rotationXInput.value;
  const ry = rotationYInput.value;
  const sliceH = sliceHeightInput.value;
  const fileName = `kupola_freq${freq}_rotX${rx}_rotY${ry}_sliceH${sliceH}.stl`;
  const blob = new Blob([stlString], {type: 'text/plain'});
  const link = document.createElement('a');
  link.href = URL.createObjectURL(blob);
  link.download = fileName;
  link.click();
  URL.revokeObjectURL(link.href);
}

// Event listeners for buttons
document.getElementById('showBtn').addEventListener('click', () => {
  pushState();
  clearRedoStack();
  const freq = parseInt(document.getElementById('frequency').value);
  createDome(freq);
  applyRotationToDome();
  updateRotationInputs();
  updateSlicePlane();
});

document.getElementById('sliceBtn').addEventListener('click', () => {
  pushState();
  clearRedoStack();
  sliceDome();
});

document.getElementById('undoBtn').addEventListener('click', () => {
  let state = popState();
  if(state) {
    pushRedoState({
      tris: currentTris.map(tri => tri.map(v => v.clone())),
      freq: currentFreq,
      rotationX: rotation.x,
      rotationY: rotation.y,
      sliceHeight: parseFloat(sliceHeightInput.value),
      sliceRotX: parseFloat(sliceRotXInput.value),
      sliceRotY: parseFloat(sliceRotYInput.value),
      sliceRotZ: parseFloat(sliceRotZInput.value)
    });
    restoreState(state);
  }
});

document.getElementById('redoBtn').addEventListener('click', () => {
  let state = popRedoState();
  if(state) {
    pushState();
    restoreState(state);
  }
});

document.getElementById('exportBtn').addEventListener('click', () => {
  exportSTL();
});

// Update slicePlane and line when slice inputs change
sliceHeightInput.addEventListener('input', () => {
  updateSlicePlane();
});
sliceRotXInput.addEventListener('input', () => {
  updateSlicePlane();
});
sliceRotYInput.addEventListener('input', () => {
  updateSlicePlane();
});
sliceRotZInput.addEventListener('input', () => {
  updateSlicePlane();
});

// Keyboard controls for rotation
window.addEventListener('keydown', e => {
  const step = THREE.MathUtils.degToRad(1);
  switch(e.key) {
    case 'ArrowUp': rotation.x -= step; updateRotationInputs(); break;
    case 'ArrowDown': rotation.x += step; updateRotationInputs(); break;
    case 'ArrowLeft': rotation.y -= step; updateRotationInputs(); break;
    case 'ArrowRight': rotation.y += step; updateRotationInputs(); break;
  }
});

// Window resize
window.addEventListener('resize', () => {
  camera.aspect = (window.innerWidth - 300) / window.innerHeight;
  camera.updateProjectionMatrix();
  renderer.setSize(window.innerWidth - 300, window.innerHeight);
});

function animate(){
  requestAnimationFrame(animate);
  domeGroup.rotation.x = rotation.x;
  domeGroup.rotation.y = rotation.y;
  renderer.render(scene, camera);
}

animate();

// Init: show ico 0 freq
createDome(0);
updateRotationInputs();
updateSlicePlane();
applyRotationToDome();

</script>
</body>
</html>