U svetlu preživljavanja, svaka tvorevina — od suncokreta do školjke, od šišarke do galaksije — mora da se izbori za prostor, za svetlost, za energiju. Mora da se uklopi u svet u kome je sve već zauzeto, i da to učini tako da ne ugrozi sebe, ali ni druge. I baš u tom izazovu opstanka, priroda ne bira ni silu ni nasilje — bira raspored. Bira oblik.

Fibonacci je odgovor na pitanje: Kako postojati, a ne smetati? Kako rasti, a ne rušiti? Kako zauzeti prostor, a ne isključivati?
To je obrazac u kome svaki novi deo zna svoje mesto. Nema ponavljanja, nema preklapanja, nema gubitka. Svaki novi element poštuje prethodni, ali i stvara uslove za naredni. To je lekcija iz harmonije među razlikama.

U tom poretku, nema diktata, nema centra koji komanduje. Ipak, sve deluje kao da neko vodi računa o celini. Baš kao u društvu koje funkcioniše kada svaki član zna svoju ulogu i deluje u skladu sa celinom, tako i suncokret postavlja svaku svoju semenku tačno tamo gde će doneti najviše koristi, bez da ijednu drugu ugrozi.

U svetu prepunom entropije, raspada i borbe, Fibonacci je tiho prisećanje da postoji red koji ne nameće, već prožima. Red koji ne dominira silom, već opstaje zahvaljujući ravnoteži. U tom redu nema krajnosti — samo večna tranzicija, spiralno kretanje koje ne vodi u krug, već napred, u širinu i u dubinu.

Zato je Fibonacci više od matematičkog niza. On je arhetip prirodnog zakona, iskonska mapa rasta koji poštuje svet u kome se odvija. On nas uči da je preživljavanje najuspešnije ne kada pobeđujemo druge, već kada nalazimo svoje mesto u širem sistemu.

Suncokret i Fibonacci niz — matematička harmonija prirode

Suncokret je jedan od najlepših primera kako se u prirodi pojavljuje matematička struktura — i to kroz Fibonacci niz, zlatni ugao i spiralni raspored semenki.

1. Spiralni raspored semenki

Na glavici suncokreta možeš uočiti dve vrste spirala:

• Spirale koje idu ulevo
• Spirale koje idu udesno

Brojevi spirala najčešće su uzastopni brojevi iz Fibonacci niza:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …

Na primer: 34 spirale ulevo i 55 udesno.

2. Kako biljka „zna“ gde da postavi semenku?

Biljka ne zna, ali svaka nova semenka se postavlja pod stalnim uglom u odnosu na prethodnu. Taj ugao se zove zlatni ugao:

gde je zlatni rez (grčko slovo φ — phi):

Računica daje:

To znači da se svaka semenka postavlja pod uglom od približno 137.5° u odnosu na prethodnu — i uvek u istom smeru.

3. Geometrijski raspored (polarno koordinatni sistem)

Svaka semenka ima svoje polarne koordinate:

koje se zatim pretvaraju u kartezijanske (x, y):

Ovaj raspored formira prirodne spirale bez preklapanja i praznina.

4. Zašto Fibonacci brojevi?

Broj spirala u levo i desno su Fibonacci brojevi jer:

• Ugao 137.5° je iracionalan — nikad se ne poklapa
• Raspored je kvazi-periodičan i vodi do optimalnog pakovanja

I zato se pojavljuju 13, 21, 34, 55 spirala i tako dalje.

Matematički:

što znači da odnosi između uzastopnih Fibonacci brojeva teže zlatnom rezu.

5. Biološki razlog: Efikasnost

Priroda nije slučajna. Evolucija favorizuje oblike koji su:

• Efikasni u pakovanju
• Optimalni u pristupu svetlosti i hranljivim materijama
• Strukturno stabilni

Raspored semenki po zlatnom uglu i Fibonacci brojevima obezbeđuje upravo to.

Suncokret koristi čisto matematičko pravilo za raspored svojih semenki:

• 137.5° zlatni ugao
• Spirale po Fibonacci brojevima
• Geometrijski optimalan, estetski savršen obrazac

Priroda, na svom jeziku, koristi matematiku da bi postigla savršenstvo.

Evo jednostavnog Python 3 koda koji simulira suncokret korišćenjem zlatnog ugla i rasporeda semenki prema Fibonacci principu:

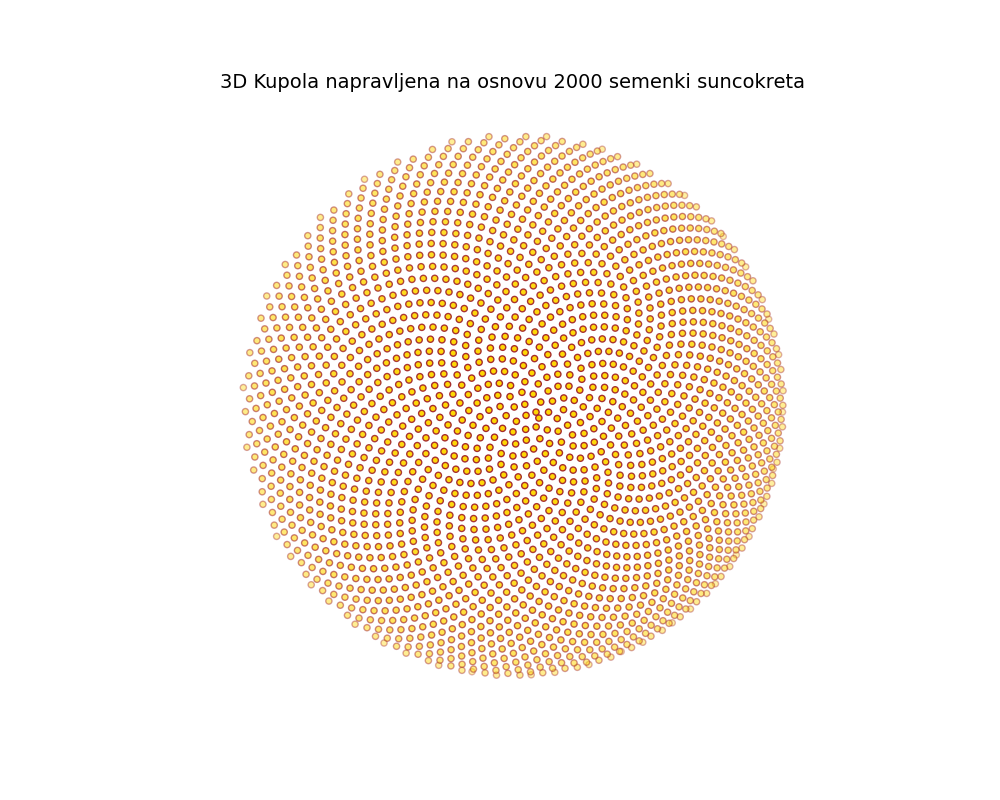
🌻 Suncokret — Spiralni raspored semenki i kupola napravljena na osnovu njih

# The MIT License (MIT)
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovim se omogućava bilo kome da koristi, kopira, menja, spaja, objavljuje,
# distribuira, daje podlicencu i/ili prodaje kopije ovog softverskog programa,
# uz uslov da u svim kopijama ili značajnim delovima softverskog programa bude
# uključena sledeća obavest:
#
# Copyright (c) 2025 Aleksandar Maričić
#
# Ovaj softverski program je pružen "takav kakav jeste", bez bilo kakvih garancija,
# izričitih ili impliciranih, uključujući, ali ne ograničavajući se na, garancije o
# prikladnosti za prodaju ili pogodnosti za određenu svrhu. U svakom slučaju, autori
# ili nosioci prava nisu odgovorni za bilo kakvu štetu ili druge obaveze koje mogu nastati
# usled upotrebe ovog softverskog programa.


import numpy as np
import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D  # neophodno za 3D plotove

num_seeds = 2000
golden_angle = np.pi * (3 - np.sqrt(5))  # ≈ 2.39996 rad = 137.5°

x = []
y = []

for n in range(num_seeds):
    r = np.sqrt(n)
    theta = n * golden_angle
    x.append(r * np.cos(theta))
    y.append(r * np.sin(theta))

x = np.array(x)
y = np.array(y)

# Normalizuj radijus da kupola bude u okviru poluprečnika R=1
r_vals = np.sqrt(x**2 + y**2)
r_max = np.max(r_vals)
x_norm = x / r_max
y_norm = y / r_max
r_norm = r_vals / r_max

R = 1  # poluprečnik kupole

# Izračunaj z koordinate na sferi poluprečnika R (gornja polulopta)
z = np.sqrt(np.maximum(0, R**2 - r_norm**2))

# Prikaz 3D kupole
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x_norm, y_norm, z, c='gold', edgecolors='brown', s=20)

ax.set_box_aspect([1,1,0.5])  # omjer osa za lepši izgled
ax.axis('off')
plt.title(f"3D Kupola napravljena na osnovu {num_seeds} semenki suncokreta", fontsize=14)
plt.show()

Ovaj program vizuelno prikazuje formiranje suncokretne spirale koristeći matematičku strukturu poznatu kao Fibonacci raspored i zlatni ugao (oko 137,5°), što rezultira elegantnom i prirodno efikasnom raspodelom tačaka. Animacija simulira postepeno nicanje semenki, pri čemu se svaka nova tačka smešta na osnovu svog rednog broja, udaljenosti od centra (koren rednog broja) i ugla rotacije. Vizuelni efekat pojačan je postepenim povećanjem veličine i promenom boje tačaka kako bi se istakla dinamika rasta. Program koristi biblioteku matplotlib i FuncAnimation za glatku animaciju, dok jasno podešene granice prikaza i pravilna inicijalizacija garantuju ispravno funkcionisanje bez grešaka. Rezultat je vizuelno privlažna i matematički zasnovana animacija koja odražava način na koji priroda organizuje prostor.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

# Broj semenki
num_seeds = 2000
# Zlatni ugao (≈ 137,5°)
golden_angle = np.pi * (3 - np.sqrt(5))

# Koordinate, boje i veličine
n = np.arange(num_seeds)
r = np.sqrt(n)
theta = n * golden_angle
x = r * np.cos(theta)
y = r * np.sin(theta)
colors = np.linspace(0, 1, num_seeds)
sizes = 10 + 15 * colors       # tačke malo veće ka spolja

# Figura i osa
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_facecolor('white')
ax.axis('off')
ax.set_aspect('equal')

# >>> Кључно: прошири границе тако да укључе све тачке <<<
margin = 1        # мала резерва око најдаље тачке
ax.set_xlim(x.min() - margin, x.max() + margin)
ax.set_ylim(y.min() - margin, y.max() + margin)

# Почетни празан scatter
scatter = ax.scatter([], [], s=[], c=[], cmap='plasma',
                     alpha=0.8, edgecolors='none')

def init():
    scatter.set_offsets(np.empty((0, 2)))
    scatter.set_sizes([])
    scatter.set_array([])
    return scatter,

def update(frame):
    scatter.set_offsets(np.column_stack((x[:frame], y[:frame])))
    scatter.set_sizes(sizes[:frame])
    scatter.set_array(colors[:frame])
    return scatter,

anim = FuncAnimation(fig, update,
                     frames=range(1, num_seeds + 1),
                     init_func=init,
                     interval=20, blit=False, repeat=False)

plt.title(f"Animacija suncokretne spirale: {num_seeds} semenki",
          fontsize=14)
plt.show()