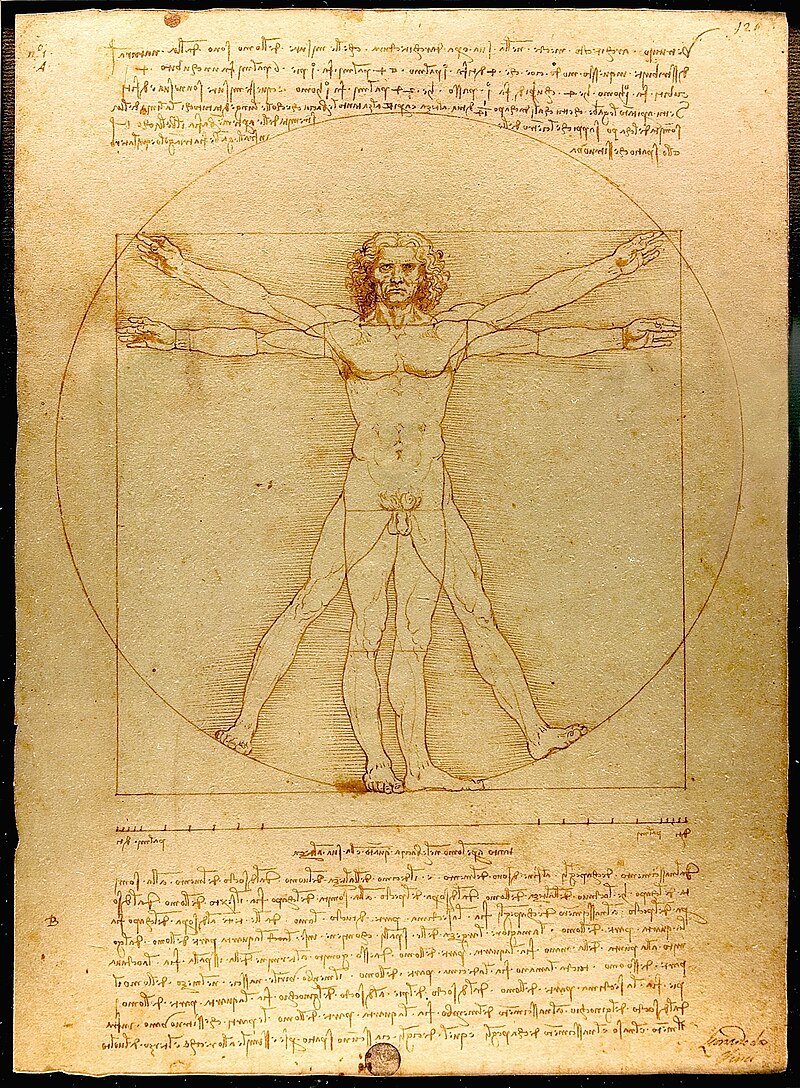
Vitruvijev čovek, čuvena ilustracija Leonarda da Vinčija, simbol je savršene proporcije ljudskog tela u skladu sa zakonima prirode i geometrije. Inspirisan radovima rimskog arhitekte Vitruvija, Da Vinči je prikazao telo koje se istovremeno uklapa u krug i kvadrat — dva osnovna geometrijska oblika. U ovom crtežu prisutni su brojni odnosi koji se približno poklapaju sa zlatnim presekom (φ ≈ 1.618), univerzalnom proporcijom koja se često javlja u prirodi, umetnosti i arhitekturi. Ova veza između anatomije i matematike osvetljava ideju da je ljudsko telo model harmonične ravnoteže i estetske savršenosti.
Zlatni presek u dimenzijama ljudskog tela
Zlatni presek, poznat kao sectio aurea ili φ, ima vrednost: \[ \phi = \frac{1 + \sqrt{5}}{2} \approx 1.618 \] i često se pojavljuje u prirodi, umetnosti i arhitekturi. Leonardo da Vinči je, u duhu renesansne filozofije, zlatni presek primenio i na proporcije ljudskog tela, naročito u svom crtežu Vitruvijev čovek.
Vitruvijeve proporcije i čovek kao geometrijski model
Prema rimskom arhitekti Vitruviju, idealne proporcije ljudskog tela mogu se izraziti u odnosu na geometrijske oblike — krug i kvadrat. Leonardo je interpretirao ove proporcije i kroz precizne matematičke odnose:
- Rastojanje od temena do pupka = \( \frac{1}{2} \cdot h \)
- Širina ramena = \( \frac{1}{4} \cdot h \)
- Dužina glave = \( \frac{1}{8} \cdot h \)
- Dužina podlaktice = dužina stopala
- Ukupna visina tela = raspon ruku
Zlatni odnosi u ljudskom telu
Mnogi delovi ljudskog tela približno slede zlatni presek. Ovo se ne odnosi samo na ceo rast, već i na pojedinačne delove tela:
| Odnos | Formula | Vrednost ≈ φ |
|---|---|---|
| Ukupna visina / visina do pupka | \( \frac{h}{h – h/\phi} \) | \( \phi \) |
| Od pupka do poda / od pupka do temena | \( \frac{h – h/\phi}{h/\phi} \) | \( \phi \) |
| Ukupna ruka / podlaktica | \( \frac{\text{nadlaktica} + \text{podlaktica}}{\text{podlaktica}} \) | \( \phi \) |
| Dužina šake / dužina članka | \( \frac{\text{saka}}{\text{slanak}} \) | \( \phi \) |
I lice često sledi zlatne odnose, na primer: \[ \frac{\text{rastojanje od ociju do brade}}{\text{rastojanje od ociju do vrha glave}} \approx \phi \]
Upisivanje tela u krug i kvadrat
U Leonardovom crtežu, čovek je upisan u kvadrat (skupljene noge) i krug (raširene noge i ruke). Centar kvadrata je u preponama, a centar kruga u pupku. To omogućava da se mnoge telesne dimenzije izraze kao funkcije zlatnog preseka.
Kada su noge raširene da dodiruju obod kruga, one formiraju trougao sa vrhom u pupku i osnovicom između stopala. To je gotovo jednakokraki trougao čiji se odnosi takođe mogu dovesti u vezu sa φ.
Ako su kraci trougla dužine \( a \), a osnovica \( b \), tada: \[ \frac{a}{b} \approx \phi \quad \text{(zlatni trougao)} \] ili obrnuto: \[ \frac{b}{a} \approx \phi \quad \text{(reverzni zlatni trougao)} \]
U slučaju da je ugao između nogu oko \( 72^\circ \), trougao odgovara jednom od trouglova u pravilnom pentagramu — što dodatno potvrđuje prisustvo zlatnog preseka u kompoziciji tela.
Ljudsko telo, kada se analizira kroz geometriju, pokazuje neverovatne srazmere koje se mogu dovesti u vezu sa zlatnim presekom. Leonardo da Vinči je, kroz Vitruvijevog čoveka, spojio umetnost, proporciju i matematiku u jedinstveni model čoveka kao mere svih stvari. Trougao raširenih nogu samo je jedan od mnogih primera gde se φ pojavljuje u ljudskoj anatomiji.
Leonardove proporcije ljudskog tela predstavljaju jedinstvenu harmoniju između prirodnih odnosa tela i univerzalnih matematičkih konstanti, posebno zlatnog preseka (označenog sa φ). Zlatni presek se definiše kao:
\(\displaystyle \phi = \frac{1 + \sqrt{5}}{2} \approx 1.618 \)
Osnovna ideja zlatnog preseka jeste da celina prema većem delu stoji u istom odnosu kao veći deo prema manjem:
\(\displaystyle \frac{a + b}{a} = \frac{a}{b} = \phi \)
U Leonardovim proporcijama:
- visina tela = \(h = 24\) dlana
- 1 dlan = \(\frac{1}{24}h\)
- 1 stopalo = 4 dlana = \(\frac{1}{6}h\)
- raspon ruku = \(h\)
Ovi odnosi su sami po sebi racionalni, ali u okviru ukupne visine tela može se primetiti kako mnogi odnosi reflektuju zlatni presek ili njegove reciproke.
Pupak i zlatni presek
Jedna od najpoznatijih Leonardo-Vitruvijevih podela je visina do pupka:
\(\displaystyle \text{visina do pupka} = \frac{h}{\phi} \approx 0.618\,h \)
\(\displaystyle \text{ostatak do glave} = h – \frac{h}{\phi} = \frac{h}{\phi^2} \approx 0.382\,h \)
Tako telo biva podeljeno na dva dela u savršenom odnosu zlatnog preseka:
\(\displaystyle \frac{\text{celina}}{\text{veci deo}} = \frac{\text{veci deo}}{\text{manji deo}} = \phi \)
- dužina šake = \(\frac{1}{10}h \approx 0.618^3 h\)
- dužina stopala = \(\frac{1}{6}h \approx 0.618^2 h\)
- razdaljina brada-teme = \(\frac{1}{8}h \approx \frac{1}{\phi^2 + \phi} h\)
- razmak kosa-brada = \(\frac{1}{10}h \approx 0.618^3 h\)
- razmak vrat-kosa = \(\frac{1}{6}h \approx 0.618^2 h\)
- širina ramena = \(\frac{1}{4}h \approx 0.618^1 h\)
- prsa-teme = \(\frac{1}{4}h \approx 0.618 h\)
- lakat-šaka = \(\frac{1}{4}h \approx 0.618 h\)
- lakat-pazuh = \(\frac{1}{8}h \approx 0.382 h = \frac{1}{\phi^2}h\)
- dužina lica = \(\frac{1}{10}h\), sa unutrašnjim deljenjem:
- kosa-obrve: \(\frac{1}{3} \times \frac{1}{10}h = \frac{1}{30}h \approx \frac{1}{\phi^3}h\)
- brada-nos: \(\frac{1}{3} \times \frac{1}{8}h = \frac{1}{24}h \approx \frac{1}{\phi^3}h\)
Leonardove proporcije nisu samo estetski utemeljene, već se velik broj njih može izraziti kao približni stepeni zlatnog preseka: \(\phi^n\) i \(\frac{1}{\phi^n}\), gde je \(n \in \mathbb{N}\). Ova matematička harmonija podržava ideju da ljudsko telo predstavlja model univerzalne ravnoteže brojeva, proporcija i prirodne lepote.
Povezanost zlatnog preseka i Fibonaccijevog niza
Fibonaccijev niz \((F_n)\) definiše se rekurentno:
\[ F_0 = 0, \quad F_1 = 1, \quad \text{i za } n \geq 2: \quad F_n = F_{n-1} + F_{n-2} \]
Odnosi susednih članova niza približavaju se zlatnom preseku \(\phi\):
\[ \lim_{n \to \infty} \frac{F_{n+1}}{F_n} = \phi = \frac{1 + \sqrt{5}}{2} \approx 1.618 \]
Matematički dokaz koristeći Binetovu formulu
Binetova formula daje zatvoreni izraz za \(F_n\):
\[ F_n = \frac{\phi^n – \psi^n}{\sqrt{5}} \]
gde je
\[ \phi = \frac{1 + \sqrt{5}}{2}, \quad \psi = \frac{1 – \sqrt{5}}{2} \]
Računajmo odnos susednih članova:
\[ \frac{F_{n+1}}{F_n} = \frac{\frac{\phi^{n+1} – \psi^{n+1}}{\sqrt{5}}}{\frac{\phi^n – \psi^n}{\sqrt{5}}} = \frac{\phi^{n+1} – \psi^{n+1}}{\phi^n – \psi^n} = \frac{\phi^{n} \cdot \phi – \psi^{n} \cdot \psi}{\phi^n – \psi^n} \]
Delimo brojilac i imenilac sa \(\phi^n\):
\[ \frac{F_{n+1}}{F_n} = \frac{\phi – \psi^n \psi / \phi^n}{1 – (\psi / \phi)^n} \]
Pošto je \(|\psi / \phi| < 1\), pri \(n \to \infty\) važi:
\[ \lim_{n \to \infty} \frac{F_{n+1}}{F_n} = \phi \]
Ovo pokazuje da odnos susednih Fibonaccijevih brojeva teži vrednosti zlatnog preseka \(\phi\).
Matematička veza između zlatnog preseka, Fibonaccijevog niza i Vitruvijevog čoveka
Vitruvijev čovek prikazuje proporcije ljudskog tela zasnovane na univerzalnim harmonijama i pravilima geometrije. Leonardo da Vinci je uočio da mnogi odnosi unutar ljudskog tela približno prate zlatni presek \(\phi\).
Zlatni presek definiše se kao:
\[ \phi = \frac{1 + \sqrt{5}}{2} \approx 1.618 \]
Fibonaccijev niz \((F_n)\) je niz prirodnih brojeva definisan rekurentno:
\[ F_0 = 0, \quad F_1 = 1, \quad F_n = F_{n-1} + F_{n-2} \quad \text{za } n \geq 2 \]
Odnosi susednih članova Fibonaccijevog niza približavaju se zlatnom preseku:
\[ \lim_{n \to \infty} \frac{F_{n+1}}{F_n} = \phi \]
Primeri proporcija u ljudskom telu prema Vitruvijevom čoveku
- Dužina šake približno je \(\frac{1}{10}\) ukupne visine, što je blizu \(\phi^3\).
- Visina do pupka je približno \(\frac{1}{\phi}\) ukupne visine tela.
- Širina ramena i drugi segmenti tela mogu se izraziti kao recipročni ili stepeni \(\phi\).
Matematička interpretacija
Ljudsko telo može se posmatrati kao podeljeno na segmente čije dužine prate odnose susednih članova Fibonaccijevog niza, tj.
\[ \dots, \frac{F_{n+1}}{F_n}, \quad \frac{F_n}{F_{n-1}}, \quad \dots \quad \longrightarrow \quad \phi \]
Ove proporcije stvaraju harmoniju i ravnotežu, koju je Leonardo izrazio kroz Vitruvijevog čoveka kao model univerzalne lepote i prirodnog poretka.
Proporcije šire od ruku: Širina ramena i drugi segmenti izraženi kroz zlatni presek \(\phi\)
Zlatni presek \(\phi = \frac{1+\sqrt{5}}{2} \approx 1.618\) je matematička konstanta koja se često pojavljuje u prirodi i umetnosti, uključujući i proporcije ljudskog tela. Pored poznatih odnosa dužine ruku i visine, i širina ramena i drugi segmenti tela mogu se približno izraziti kao recipročni ili stepeni \(\phi\).
Recipročni odnosi
Recipročni odnosi su oblici izraženi kao \(\frac{1}{\phi^n}\), gde je \(n\) prirodan broj. Ovi odnosi opisuju manje segmente tela u odnosu na ukupnu visinu \(h\). Na primer:
- Visina do lakta prema ukupnoj visini: \[ \approx \frac{1}{\phi} \cdot h \approx 0.618\, h \]
- Dužina šake u odnosu na visinu: \[ \approx \frac{1}{\phi^3} \cdot h \approx 0.236\, h \]
- Razdaljina lakat-pazuh: \[ \approx \frac{1}{\phi^2} \cdot h \approx 0.382\, h \]
Stepeni \(\phi\)
Segmenti koji su veći, ili koji čine osnovne proporcije tela, mogu se izraziti kao pozitivni stepeni \(\phi^n\). Ovo su odnosi veće dužine u telu, npr.:
- Širina ramena u odnosu na visinu: \[ \approx \phi^{-1} \cdot h = \frac{1}{\phi} \cdot h \approx 0.618\, h \] (širina ramena često se uzima kao oko 1/4 visine, što je u blizini \(\phi^{-1}\))
- Razmak od temena do grudi: \[ \approx \phi^{0} \cdot h = 1 \cdot h = h \] (celo telo je naravno 1 = \(\phi^0\))
- Raspon ruku (širina sa ispruženim rukama): \[ \approx \phi^{1} \cdot h \approx 1.618\, h \] (mada u klasičnim proporcijama ovo je obično jednako visini, ali u nekim varijantama može se posmatrati kao \(\phi\) razmera)
Izrazi proporcija tela kroz stepeni i recipročne vrednosti \(\phi\) pružaju elegantan matematički okvir koji objašnjava harmoniju i estetsku privlačnost ljudskih proporcija. Ovo je jedan od razloga zašto Leonardo da Vinci i drugi umetnici i naučnici veruju da zlatni presek modeluje savršen balans prirode i umetnosti, posebno u ljudskom telu kao što je ilustrirano u Vitruvijevom čoveku.
Linkovi:
Rory Mac Sweeney: Leonardo’s Vitruvian Man: modern craniofacial anatomical analysis reveals a possible solution to the 500-year-old mystery
https://www.tandfonline.com/doi/full/10.1080/17513472.2025.2507568