U oktobru 2008, osoba (ili grupa) pod pseudonimom Satoshi Nakamoto objavljuje rad pod nazivom:
“Bitcoin: A Peer-to-Peer Electronic Cash System”
PDF je dostupan javno i danas.
U tom radu se predlaže:
- Digitalna valuta bez posrednika (banaka)
- Sistem u kojem korisnici direktno šalju novac jedni drugima
- Upotreba kriptografije i distribuirane mreže da bi se sprečila prevara
U tom trenutku – finansijska kriza potresa svet, i mnogi gube poverenje u banke i vlade.
Kako bih sebi razjasnio Bitkoin, s obzirom na to da mi je mnogo toga bilo nejasno, za početak sam preveo originalni rad Satoshi Nakamotoa na osnovu kojeg je Bitkoin nastao.
Bitcoin: Elektronski novac zasnovan na direktnoj razmeni među korisnicima
Satoshi Nakamoto
satoshin@gmx.com
www.bitcoin.org
Apstrakt:
Potpuno direktan (peer-to-peer) elektronski novac omogućio bi slanje uplata sa jednog korisnika direktno drugom, bez potrebe za finansijskom institucijom kao posrednikom. Digitalni potpisi rešavaju deo problema, ali ako i dalje postoji poverenje u treću stranu koja sprečava dvostruku potrošnju istog novca, gubi se glavna prednost sistema. Mi predlažemo rešenje problema dvostruke potrošnje korišćenjem peer-to-peer mreže. Ta mreža vremenski obeležava transakcije tako što ih umeće u neprekidni lanac koji je zasnovan na kriptografskom dokazivanju rada (proof-of-work). Taj lanac predstavlja zapis koji nije moguće menjati bez ponovnog izvođenja ovog dokazivanja rada. Najduži lanac ne samo što dokazuje redosled događaja, već i da je nastao zahvaljujući najvećoj računarskoj snazi u mreži. Dok većinu računarske snage kontrolišu korisnici koji nisu udruženi da napadnu mrežu, oni će stvarati najduži lanac i nadmašiće eventualne napadače. Sama mreža ne zahteva kompleksnu strukturu. Poruke se šalju na najbolji mogući način, a čvorovi (nodi) mogu slobodno ulaziti i izlaziti iz mreže, prihvatajući najduži lanac kao dokaz šta se dogodilo dok nisu bili povezani.
1. Uvod
Internet trgovina danas skoro isključivo zavisi od finansijskih institucija koje služe kao poverljivi posrednici u procesiranju elektronskih uplata. Iako sistem uglavnom funkcioniše, on pati od slabosti koje su inherentne modelu zasnovanom na poverenju. Potpuno nepovratne transakcije zapravo nisu moguće, jer finansijske institucije moraju da posreduju u rešavanju sporova. Taj posrednički proces povećava troškove transakcija, što ograničava minimalnu praktičnu veličinu uplata i onemogućava male, povremene transakcije. Širi problem je i gubitak mogućnosti za nepovratna plaćanja za usluge koje takođe nisu nepovratne. Zbog mogućnosti poništavanja, poverenje se mora proširiti. Prodavci moraju biti oprezni prema kupcima i tražiti od njih više informacija nego što bi inače bilo potrebno. U sistemu je prihvaćeno da će deo prevara uvek postojati. Ove troškove i neizvesnosti pri plaćanju može se izbeći korišćenjem fizičkog novca, ali ne postoji način za plaćanje preko komunikacionih kanala bez poverljivog posrednika.
Ono što nam treba je elektronski platni sistem zasnovan na kriptografskom dokazu, a ne na poverenju, koji omogućava bilo koje dve zainteresovane strane da razmene sredstva direktno, bez potrebe za poverljivom trećom stranom. Transakcije koje je praktično nemoguće poništiti zaštitile bi prodavce od prevara, dok bi uobičajeni sistemi escrow-a (depozita) lako štitili kupce. U ovom radu predlažemo rešenje problema dvostruke potrošnje korišćenjem distribuiranog peer-to-peer servera za vremensko označavanje, koji kreira kriptografski dokaz hronološkog redosleda transakcija. Sistem je siguran sve dok pošteni korisnici zajedno kontrolišu više računarske snage nego bilo koja grupa napadača koji se udruže.
2. Transakcije
Elektronski novčić definišemo kao niz digitalnih potpisa. Svaki vlasnik prenosi novčić na sledećeg tako što digitalno potpisuje haš prethodne transakcije i javni ključ narednog vlasnika, i dodaje te podatke na kraj novčića. Primalac može proveriti potpise kako bi potvrdio celokupan lanac vlasništva.
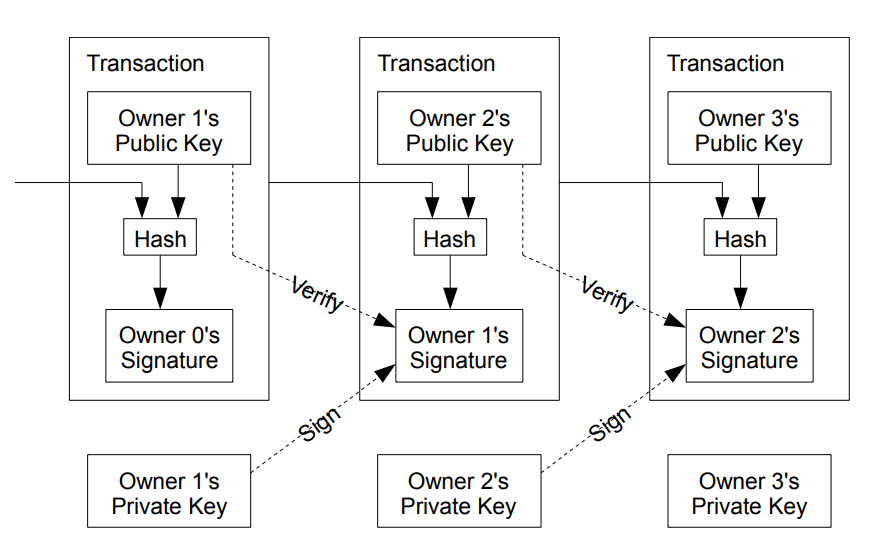
Problem je, naravno, što primalac ne može da proveri da li neki od prethodnih vlasnika nije potrošio isti novčić dva puta.
Uobičajeno rešenje je uvođenje poverljive centralne institucije, ili kovačnice (mint), koja proverava svaku transakciju da spreči dvostruku potrošnju. Posle svake transakcije, novčić mora da se vrati kovačnici koja izdaje novi novčić, i samo novčići direktno izdati od strane kovačnice smatraju se sigurnim i nepovredivim.
Međutim, problem sa ovim pristupom je što cela sudbina novčanog sistema zavisi od firme koja upravlja kovačnicom, jer svaka transakcija mora da prođe preko nje, kao što je slučaj sa bankama.
Nama treba način da primalac bude siguran da prethodni vlasnici nisu potpisivali ranije transakcije. Za nas je važna samo prva (najranija) transakcija, pa nam nije bitno ako neko kasnije pokuša da potroši isti novčić još jednom. Jedini način da se potvrdi da neka ranija transakcija nije postojala jeste da smo upoznati sa svim transakcijama.
U modelu sa kovačnicom, ona je bila upoznata sa svim transakcijama i odlučivala koja je prva stigla. Da bismo to postigli bez poverljive treće strane, transakcije moraju biti javno objavljene, a potrebno nam je i da učesnici postignu saglasnost o jednoj jedinoj istoriji i redosledu primljenih transakcija. Primalac mora imati dokaz da je u trenutku svake transakcije većina čvorova (noda) potvrdila da je to bila prva primljena transakcija.
3. Server za vremensko označavanje (timestamp server)
Rešenje koje predlažemo počinje sa serverom za vremensko označavanje. Takav server radi tako što uzima haš grupe podataka koje treba vremenski obeležiti i široko objavljuje taj haš, na primer u novinama ili na internetu. Taj vremenski pečat dokazuje da su podaci morali postojati u određenom trenutku, jer su uključeni u haš. Svaki sledeći vremenski pečat uključuje i prethodni haš u svoj haš, stvarajući lanac, pri čemu svaki novi pečat dodatno potvrđuje sve prethodne.
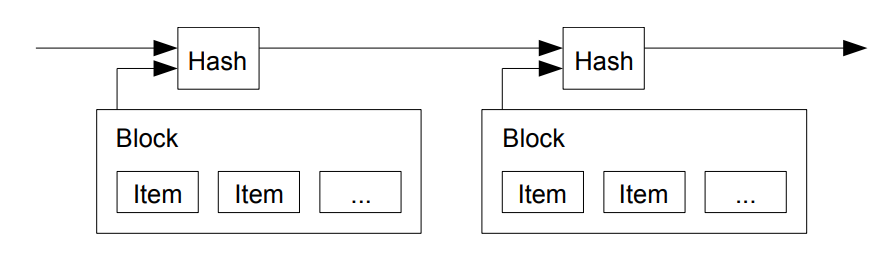
4. Dokaz o radu (Proof-of-Work)
Da bismo napravili distribuirani server za vremensko označavanje na peer-to-peer principu, moraćemo da koristimo sistem dokaza o radu sličan Adam Bekovom Hashcash-u, umesto da se oslanjamo na novinske ili internet objave.
Dokaz o radu podrazumeva traženje vrednosti koja, kada se hasira (na primer sa SHA-256), daje haš koji počinje sa određenim brojem nula u bitovima. Prosečan rad potreban za pronalaženje te vrednosti raste eksponencijalno sa brojem traženih početnih nula, dok se ispravnost može brzo proveriti tako što se izračuna samo jedan haš.
U našoj mreži za vremensko označavanje, dokaz o radu ostvarujemo tako što povećavamo posebnu vrednost (nonce) u bloku dok ne pronađemo onu koja daje hašu bloka traženi broj početnih nula. Kada se uloži potrebni računarski napor da se blok učini validnim po pravilu dokaza o radu, blok nije moguće menjati bez ponovnog izvođenja tog posla. Kako se kasniji blokovi nižu iza njega, menjanje tog bloka zahtevalo bi da se ponovo izrade i svi blokovi koji su došli posle njega.
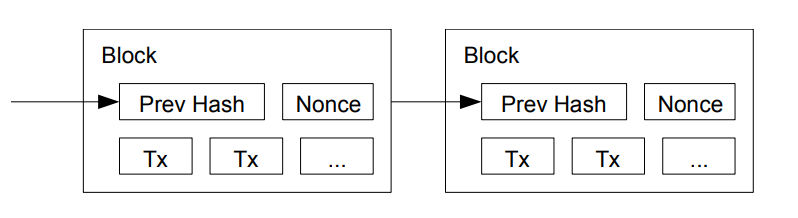
Dokaz o radu rešava i problem odlučivanja većine po pitanju zastupljenosti.
Da je većina određivana po principu „jedan IP – jedan glas“, sistem bi mogao lako biti zloupotrebljen od strane onih koji mogu da obezbede veliki broj IP adresa. Dokaz o radu u suštini znači „jedan CPU – jedan glas“. Većinu u odlučivanju predstavlja najduži lanac, u koji je uloženo najviše računske snage kroz dokaz o radu. Ako većinu računarske snage kontrolišu pošteni čvorovi, njihova iskrena verzija lanca će rasti najbrže i nadmašiće sve konkurentske lance. Da bi napadač promenio neki stari blok, morao bi da ponovo izvede dokaz o radu za taj blok i sve blokove posle njega, a zatim da stigne i prestigne rad poštenih čvorova. Kasnije ćemo pokazati da verovatnoća da sporiji napadač sustigne mrežu opada eksponencijalno kako se dodaju novi blokovi.
Da bi se prilagodila sve većoj brzini računara i promenama u interesovanju za pokretanje čvorova, teškoća dokaza o radu prilagođava se na osnovu pokretnog proseka, ciljajući određeni prosečan broj blokova po satu. Ako se blokovi prave prebrzo, težina se povećava.
5. Mreža
Koraci za funkcionisanje mreže su sledeći:
- Nove transakcije se šalju svim čvorovima.
- Svaki čvor prikuplja nove transakcije u blok.
- Svaki čvor pokušava da pronađe teško dokazivanje rada za svoj blok.
- Kada čvor pronađe validan dokaz o radu, šalje blok svim ostalim čvorovima.
- Čvorovi prihvataju blok samo ako su sve transakcije u njemu validne i nisu ranije potrošene.
- Čvorovi pokazuju da prihvataju blok tako što rade na kreiranju sledećeg bloka u lancu, koristeći haš prihvaćenog bloka kao prethodni haš.
Čvorovi uvek smatraju da je najduži lanac ispravan i nastavljaju da rade na njegovom produženju. Ako dva čvora istovremeno objave različite verzije sledećeg bloka, neki čvorovi mogu prvo da prime jednu, a neki drugu verziju. U tom slučaju rade na onoj koju su prvo primili, ali čuvaju i drugu granu u slučaju da ona postane duža. Nerazrešena situacija će se razrešiti kada se pronađe sledeći dokaz o radu i jedna grana postane duža; čvorovi koji su radili na kraćoj grani tada će preći na dužu.
Nove transakcije ne moraju obavezno da stignu do svih čvorova. Dokle god stignu do većine, ubrzo će biti uključene u blok. Slanje blokova takođe može podneti gubitak poruka — ako čvor ne primi neki blok, zatražiće ga kada primi sledeći blok i shvati da je neki propustio.
6. Podsticaj
Prva transakcija u svakom bloku je posebna i kreira novi novčić koji pripada kreatoru bloka. Ovo daje podsticaj čvorovima da podrže mrežu i pruža način za početnu distribuciju novčića u opticaju, jer ne postoji centralna institucija koja ih izdaje. Kontinuirano stvaranje stalne količine novih novčića može se uporediti sa rudarenjem zlata gde se resursi troše da bi se dodalo zlato u opticaj — kod nas se troše CPU vreme i struja.
Podsticaj se može dopuniti i transakcionim naknadama. Ako je vrednost izlaza transakcije manja od vrednosti ulaza, razlika predstavlja naknadu koja se dodaje na podsticajnu vrednost bloka koji sadrži tu transakciju. Kada unapred određeni broj novčića uđe u opticaj, podsticaj može u potpunosti preći na transakcione naknade i time biti bez inflacije.
Podsticaj takođe može pomoći da čvorovi ostanu pošteni. Ako bi neki pohlepni napadač imao više računarske snage nego svi pošteni zajedno, morao bi da bira između korišćenja te snage da prevari druge tako što bi ukrao svoja plaćanja nazad ili da je koristi za stvaranje novih novčića. Verovatno će mu biti isplativije da igra po pravilima, jer će na taj način dobiti više novih novčića nego svi drugi zajedno, nego da potkopava sistem i time urušava vrednost svoje imovine.
7. Oslobađanje prostora na disku
Kada najnovija transakcija u nekom novčiću bude dovoljno duboko u lancu blokova, stare potrošene transakcije pre nje mogu se izbaciti da bi se uštedelo mesto na disku. Da bi se to omogućilo bez narušavanja haša bloka, transakcije se haširaju u Merkle-ovom stablu, pri čemu se samo korenski haš uključuje u haš bloka. Stari blokovi se potom mogu sažimati tako što se „odseca“ deo stabla, pa unutrašnji haševi ne moraju biti sačuvani.
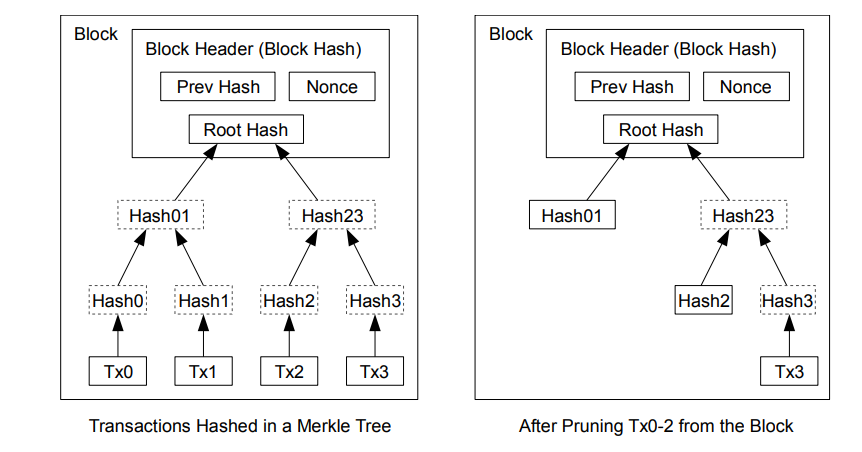
Zaglavlje bloka bez transakcija zauzima otprilike 80 bajtova.
Ako pretpostavimo da se blokovi generišu na svakih 10 minuta, to je:
80 bajtova × 6 × 24 × 365 = oko 4,2 MB godišnje.
S obzirom da su računarski sistemi u 2008. obično dolazili sa 2 GB RAM-a, a Murijev zakon predviđa rast kapaciteta od oko 1,2 GB godišnje, čuvanje zaglavlja blokova u memoriji ne bi trebalo da predstavlja problem.
8. Pojednostavljena provera plaćanja
Moguće je proveriti plaćanja bez pokretanja punog čvora mreže. Korisniku je dovoljno da čuva samo kopiju zaglavlja blokova najdužeg lanca sa dokazom o radu, koju može dobiti tako što će upitima ka čvorovima proveravati dok se ne uveri da poseduje najduži lanac. Takođe mu treba Merkle-ov ogranak (grana stabla) koja povezuje konkretnu transakciju sa blokom u kojem je vremenski označena.
Korisnik sam ne može direktno proveriti validnost transakcije, ali tako što je poveže sa mestom u lancu vidi da ju je neki čvor mreže prihvatio, a blokovi koji su došli posle dodatno potvrđuju da je transakcija prihvaćena u mreži.
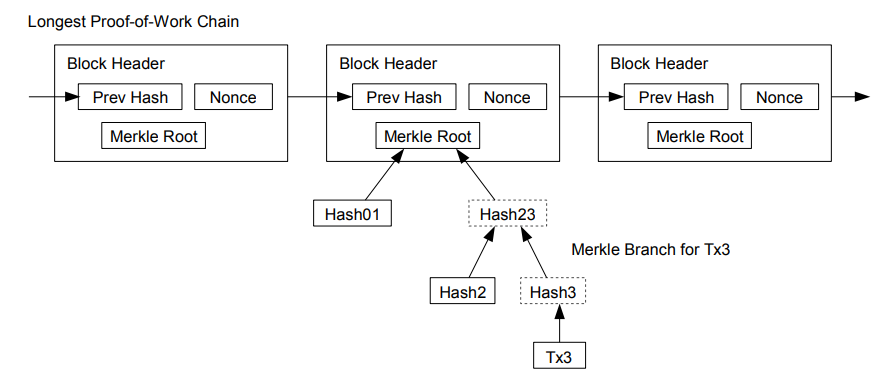
Provera je pouzdana sve dok mrežom upravljaju iskreni čvorovi, ali postaje ranjivija ukoliko napadač preuzme kontrolu nad mrežom. Iako mrežni čvorovi mogu sami proveravati transakcije, pojednostavljena metoda može biti prevarena lažnim transakcijama koje kreira napadač, i to onoliko dugo koliko uspeva da dominira mrežom. Jedan od načina da se zaštitimo od ovoga jeste da korisnički softver prihvata upozorenja od mrežnih čvorova kada oni detektuju nevalidan blok, što bi podstaklo korisnikov softver da preuzme ceo blok i te sumnjive transakcije kako bi potvrdio nepravilnost. Preduzeća koja često primaju uplate verovatno će želeti da pokreću sopstvene čvorove radi nezavisnije sigurnosti i brže provere.
9. Spajanje i deljenje vrednosti
Iako bi bilo moguće tretirati svaku kovanicu pojedinačno, bilo bi nepraktično praviti posebnu transakciju za svaki dinar u transferu. Da bi se omogućilo deljenje i spajanje vrednosti, transakcije sadrže više ulaza i izlaza. Obično postoji jedan ulaz iz veće prethodne transakcije ili više ulaza koji kombinuju manje iznose, i najviše dva izlaza: jedan za uplatu, i jedan koji vraća kusur, ukoliko postoji, nazad pošiljaocu.
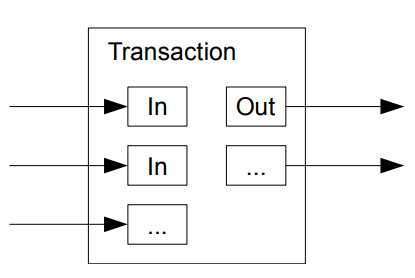
Treba napomenuti da množina zavisnosti, gde jedna transakcija zavisi od više drugih, a te transakcije opet od još većeg broja, ovde nije problem. Nikada nije potrebno izdvojiti kompletnu, samostalnu kopiju istorije neke transakcije.
10. Privatnost
Tradicionalni bankarski model ostvaruje određeni nivo privatnosti tako što ograničava pristup informacijama samo na uključene strane i poverljivu treću stranu. Obaveza javnog objavljivanja svih transakcija isključuje ovakav pristup, ali privatnost se i dalje može sačuvati na drugi način — tako što se javni ključevi drže anonimnim. Javnost može videti da neko šalje određeni iznos nekom drugom, ali bez ikakvih podataka koji povezuju transakciju sa stvarnim identitetima. Ovo je slično načinu na koji berze objavljuju informacije: vreme i veličina pojedinačnih trgovina (“tape”) su javni, ali identitet učesnika ostaje skriven.
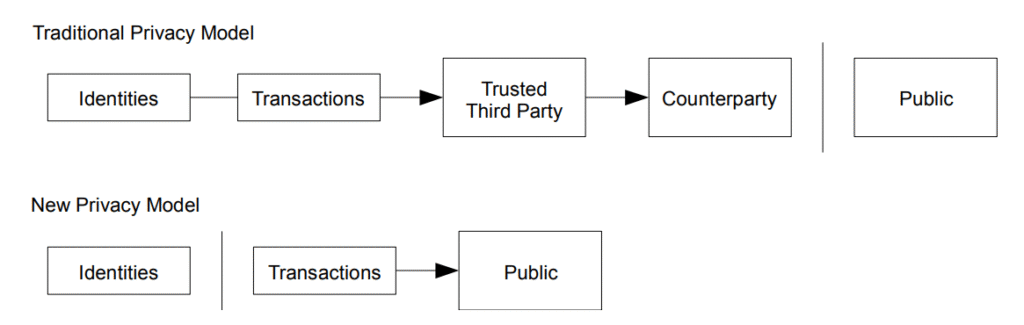
Kao dodatni „zaštitni zid“, za svaku transakciju trebalo bi koristiti novi par ključeva kako se transakcije ne bi povezivale sa istim vlasnikom. Ipak, neka povezanost je neizbežna kod transakcija sa više ulaza, jer one neizbežno otkrivaju da svi ti ulazi pripadaju istom vlasniku. Rizik je da, ako se otkrije vlasnik nekog ključa, ta povezanost može otkriti i druge transakcije koje su takođe pripadale tom vlasniku.
11. Proračuni
Razmatramo situaciju u kojoj napadač pokušava da generiše alternativni lanac brže od iskrenog lanca. Čak i ako mu to uspe, to ne znači da može proizvoljno menjati sistem — na primer, stvarati vrednost ni iz čega ili uzimati novac koji mu nikada nije pripadao. Čvorovi neće prihvatiti nevalidnu transakciju kao uplatu, a iskreni čvorovi nikada neće prihvatiti blok koji sadrži takve transakcije. Napadač može pokušati samo da promeni neku svoju transakciju da bi povratio novac koji je nedavno potrošio.
Trka između iskrenog lanca i napadačkog lanca može se opisati kao binomna slučajna šetnja (Binomial Random Walk). Uspeh je kada iskreni lanac dobije novi blok i poveća prednost za +1, a neuspeh je kada napadački lanac dobije novi blok i smanji razliku za -1.
Verovatnoća da napadač stigne do iskrenog lanca sa određenim zaostatkom analogna je problemu poznatom kao „propast kockara“ (Gambler’s Ruin). Zamislimo kockara sa neograničenim kreditom koji kreće sa minusom i igra potencijalno neograničen broj pokušaja da dođe do nule. Verovatnoću da će ikada doći do nule, odnosno da će napadač ikada stići iskreni lanac, možemo izračunati na sledeći način [8]:
- p = verovatnoća da iskreni čvor pronađe sledeći blok
- q = verovatnoća da napadač pronađe sledeći blok
- qz = verovatnoća da će napadač ikada stići iskreni lanac sa z blokova zaostatka
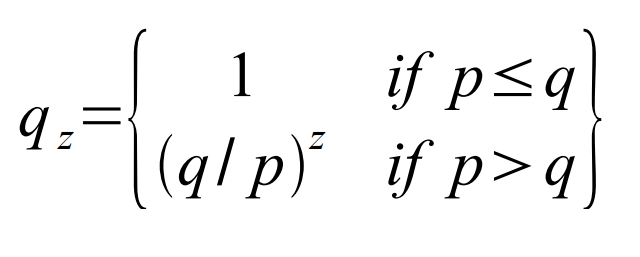
Pošto pretpostavljamo da je p > q, verovatnoća pada eksponencijalno kako se povećava broj blokova za koje napadač mora da sustigne iskreni lanac. Sa takvim šansama protiv sebe, ukoliko napadač na početku ne napravi srećan i veliki skok napred, njegove šanse postaju gotovo nepostojeće kako sve više zaostaje.
Sada razmatramo koliko primalac nove transakcije treba da sačeka pre nego što bude dovoljno siguran da pošiljalac ne može promeniti tu transakciju. Pretpostavljamo da je pošiljalac napadač koji želi da primaoca uveri da mu je platio na određeno vreme, a zatim da promeni transakciju i prebaci novac nazad sebi nakon što prođe neko vreme. Primalac će biti obavešten kada se to dogodi, ali pošiljalac se nada da će tada već biti kasno.
Primalac generiše novi par ključeva i javni ključ daje pošiljaocu neposredno pre potpisivanja transakcije. Ovo sprečava pošiljaoca da unapred pripremi lanac blokova tako što bi na njemu radio dok ne bude dovoljno srećan da napravi dovoljno dugu verziju lanca, a zatim da u tom trenutku izvrši transakciju. Nakon što se transakcija pošalje, nepošteni pošiljalac počinje u tajnosti da radi na paralelnom lancu koji sadrži alternativnu verziju njegove transakcije.
Primalac čeka dok se transakcija ne doda u blok i dok posle nje ne bude dodatih još z blokova. On ne zna tačno koliko je napadač napredovao, ali pod pretpostavkom da su iskreni blokovi dodavani prosečnim očekivanim vremenom po bloku, potencijalni napredak napadača može se opisati Poissonovom distribucijom sa očekivanom vrednošću:
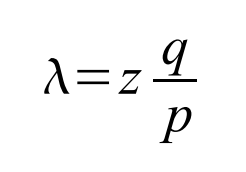
Da bismo izračunali verovatnoću da napadač još uvek može da sustigne, pomnožimo gustinu Poasonove raspodele za svaki mogući nivo napretka koji je mogao da ostvari sa verovatnoćom da bi od te tačke uspeo da sustigne iskreni lanac.
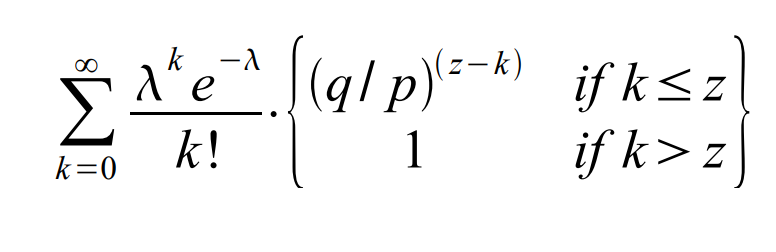
Preuređivanjem izraza kako bismo izbegli sabiranje beskonačnog repa raspodele…
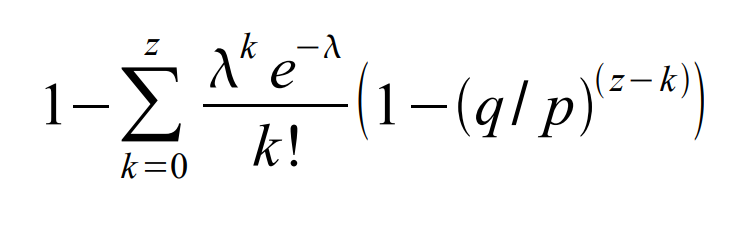
Konvertovano u C kod…
#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}
Izvršavanjem nekoliko proračuna, možemo videti da verovatnoća opadanja napada opada eksponencijalno sa porastom broja blokova z.
q=0.1 z=0 P=1.0000000 z=1 P=0.2045873 z=2 P=0.0509779 z=3 P=0.0131722 z=4 P=0.0034552 z=5 P=0.0009137 z=6 P=0.0002428 z=7 P=0.0000647 z=8 P=0.0000173 z=9 P=0.0000046 z=10 P=0.0000012 q=0.3 z=0 P=1.0000000 z=5 P=0.1773523 z=10 P=0.0416605 z=15 P=0.0101008 z=20 P=0.0024804 z=25 P=0.0006132 z=30 P=0.0001522 z=35 P=0.0000379 z=40 P=0.0000095 z=45 P=0.0000024 z=50 P=0.0000006
Izračunavanjem za slučaj kada verovatnoća padne ispod 0,1%…
P < 0.001 q=0.10 z=5 q=0.15 z=8 q=0.20 z=11 q=0.25 z=15 q=0.30 z=24 q=0.35 z=41 q=0.40 z=89 q=0.45 z=340
12. Zaključak
Predložili smo sistem za elektronske transakcije koji ne zavisi od poverenja. Krenuli smo od uobičajenog modela u kojem su „kovanice” predstavljene digitalnim potpisima, što pruža snažnu kontrolu vlasništva — ali nije dovoljno da bi se sprečilo dvostruko trošenje.
Da bismo rešili taj problem, predložili smo decentraliziranu mrežu zasnovanu na mehanizmu dokazivanja rada (proof-of-work), koja vodi javnu evidenciju transakcija. Ova istorija transakcija ubrzo postaje računarski neizvodljiva za izmene, ukoliko većinu procesorske snage drže pošteni čvorovi.
Mreža je otporna zahvaljujući svojoj jednostavnosti i nestrukturiranosti. Čvorovi rade istovremeno, bez potrebe za posebnom koordinacijom. Nije potrebno da budu identifikovani, jer poruke ne moraju biti usmerene ka određenom odredištu i dovoljno je da stignu po principu „najboljeg truda”.
Čvorovi mogu slobodno da napuštaju i ponovo pristupaju mreži, prihvatajući lanac sa dokazom rada kao potvrdu onoga što se dogodilo dok su bili odsutni. Oni „glasaju” svojom procesorskom snagom — prihvatajući važeće blokove tako što rade na njihovom produžavanju, a odbacujući nevažeće time što ih ignorišu. Svi potrebni mehanizmi pravila i podsticaja mogu se sprovoditi kroz ovaj mehanizam konsenzusa.
Reference:
[1] W. Dai, “b-money,” http://www.weidai.com/bmoney.txt, 1998.
[2] H. Massias, X.S. Avila, and J.-J. Quisquater, “Design of a secure timestamping service with minimal
trust requirements,” In 20th Symposium on Information Theory in the Benelux, May 1999.
[3] S. Haber, W.S. Stornetta, “How to time-stamp a digital document,” In Journal of Cryptology, vol 3, no
2, pages 99-111, 1991.
[4] D. Bayer, S. Haber, W.S. Stornetta, “Improving the efficiency and reliability of digital time-stamping,”
In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.
[5] S. Haber, W.S. Stornetta, “Secure names for bit-strings,” In Proceedings of the 4th ACM Conference
on Computer and Communications Security, pages 28-35, April 1997.
[6] A. Back, “Hashcash – a denial of service counter-measure,”
http://www.hashcash.org/papers/hashcash.pdf, 2002.
[7] R.C. Merkle, “Protocols for public key cryptosystems,” In Proc. 1980 Symposium on Security and
Privacy, IEEE Computer Society, pages 122-133, April 1980.
[8] W. Feller, “An introduction to probability theory and its applications,” 1957.
Prevedeno sa: https://bitcoin.org/bitcoin.pdf
