Program je zasnovan na Fibonacci algoritmu za ravnomerno raspoređivanje tačaka na sferi, što znači da može da funkcioniše za bilo koji broj tačaka nnn, a ne samo za 777. Fibonacci raspored se ne oslanja na konkretan broj tačaka, već omogućava fleksibilnost u rasporedu, sve dok nnn bude pozitivan ceo broj.
Međutim, postoje neki faktori koje treba uzeti u obzir prilikom promene broja tačaka:
1. Efikasnost (performanse):
- KDTree pretraga: Sa većim brojem tačaka, pretraga najbližih suseda pomoću KDTree algoritma može postati sporija jer broj tačaka raste. Iako je KDTree efikasan, za izuzetno velike vrednosti nnn (npr. preko miliona tačaka), performanse mogu opasti, zavisno od memorije i računarske snage.
- STL i DXF izvoz: Ako broj tačaka (i njihovih povezanih ivica) raste eksponencijalno, generisanje i izvoz u STL ili DXF fajl može postati memorijski zahtevno, jer broj cilindara (za STL) ili linija (za DXF) raste sa kvadratom broja tačaka.
2. Razmak između tačaka:
Fibonacci raspored prirodno raspoređuje tačke sa minimalnim međusobnim razmakom, što znači da sa povećanjem broja tačaka razmak između tačaka postaje manji. To može biti korisno za veoma detaljne mreže, ali može dovesti do gustih mreža sa malim razmakom kada je broj tačaka veoma velik.
3. Numerička stabilnost:
- Sa povećanjem broja tačaka može doći do numeričkih grešaka u računanju, naročito u fazama poput pretrage najbližih suseda ili izračunavanja ugla ϕi, kada se približavaju granice računarskih preciznosti.
- Na primer, za vrlo veliki broj tačaka, kod računa polarnih i azimutalnih uglova, može doći do gubitka preciznosti u računarskoj reprezentaciji brojeva.
4. Prilagodljivost za manje tačaka:
- Ako broj tačaka nnn bude mali (npr. 10-100), mreža može postati vizualno “previše razmaknuta”, i linije između tačaka će biti veće u odnosu na površinu sfere. To može učiniti 3D model manje interesantnim i preciznim u pogledu rasporeda.
Skalabilnost Fibonacijeve sfere i KD stabla
Za vrlo velike brojeve tačaka (na primer kada je \( n > 10^5 \)), Fibonacci algoritam i dalje može uspešno generisati tačke ravnomerno raspoređene po površini sfere.
Međutim, kako broj tačaka raste, može biti potrebno optimizovati kod kako bi se efikasno upravljalo memorijom, posebno tokom pretrage najbližih suseda.
U takvim slučajevima može biti korisno koristiti efikasnije algoritme za skaliranje KDTree strukture, ili razmotriti druge strukture podataka za prostornu pretragu, poput:
- Ball Tree (za gustu metriku)
- Annoy (Approximate Nearest Neighbors)
- Faiss (Facebook AI Similarity Search)
Pravilna izbor strukture zavisi od kompromisa između preciznosti i brzine pretrage, kao i od ograničenja memorije sistema.
Preporuke:
- Za manji broj tačaka: Program će raditi efikasno, sa brzom generacijom modela, ali možda vizualizacija neće biti toliko dinamična ili interesantna.
- Za veći broj tačaka: Preporučuje se testiranje performansi i praćenje memorijskih zahteva, jer će broj linija u STL i DXF fajlu rasti kvadratno sa nnn.
U suštini, program je upotrebljiv za bilo koji broj tačaka, ali može zahtevati optimizacije za veoma veliki broj tačaka, naročito kada su resursi računara ili brzina izvoza faktori ograničenja.
Zadatak:
Formirati 3D sferu sa nnn ravnomerno raspoređenih tačaka na površini koristeći Fibonacci algoritam. Za svaku tačku pronaći 6 najbližih suseda, zatim stvoriti mrežu linija (ivica) koje povezuju te tačke. Na kraju, generisati i sačuvati 3D model sfera u tri formata: DXF (linije), STL (cilindrične šipke).
Fibonacijeva sfera i KD stablo
1. Fibonacijeva distribucija tačaka na sferi
Cilj je rasporediti \( n \) tačaka ravnomerno na površini jedinicne sfere. Korišćenjem zlatnog ugla dobijamo elegantnu distribuciju poznatu kao Fibonacci sphere.
Zlatni ugao \( \theta_g \) definisan je kao: \[ \theta_g = \pi (3 – \sqrt{5}) \approx 137.5^\circ \]
Za \( i \in \{0, 1, \dots, n-1\} \), tačke se postavljaju na sferu po sledećim formulama:
\[ z_i = 1 – \frac{2(i + 0.5)}{n} \] \[ r_i = \sqrt{1 – z_i^2} \] \[ \phi_i = \theta_g \cdot i \] \[ x_i = r_i \cdot \cos(\phi_i), \quad y_i = r_i \cdot \sin(\phi_i) \] \[ \text{Tačka: } p_i = (x_i, y_i, z_i) \]
Ova konstrukcija daje gotovo ujednačen raspored tačaka na sferi bez potrebe za optimizacijom, triangulacijom ili drugim težim metodama.
2. KD stablo: prostorno pretraživačka struktura
KD stablo (k-dimensional tree) je binarno stablo koje omogućava efikasnu prostornu pretragu. Za skup tačaka \( P = \{p_1, \dots, p_n\} \subset \mathbb{R}^3 \), omogućava nam da za svaku tačku pronađemo njenih \( k \) najbližih suseda.
Pretraga koristi euklidsku metrika: \[ \|p_i – p_j\| = \sqrt{(x_i – x_j)^2 + (y_i – y_j)^2 + (z_i – z_j)^2} \]
Za svaku tačku \( p_i \), pomoću KD stabla tražimo \( k \) najbližih suseda: \[ \text{NN}_k(p_i) = \{p_{j_1}, p_{j_2}, \dots, p_{j_k}\} \] i povezujemo ih ivicama \( (p_i, p_{j_m}) \) za \( m = 1, \dots, k \).
3. Povezivanje tačaka u mrežu
Iz rezultata KD stabla formiramo skup ivica: \[ E = \left\{ \{i, j\} \mid p_j \in \text{NN}_k(p_i), \; i < j \right\} \]
Rezultat je mreža (graf) tačaka na sferi gde je svaka tačka povezana sa \( k \) najbližih suseda. Ova mreža se može vizualizovati kao 3D geodetska mreža (podseća na poliedar ili površinu molekula).
4. Primenjeni kod
U Python kodu koristi se:
- NumPy za izračunavanje koordinata
- SciPy KDTree za pretragu suseda
- Trimesh za izvoz 3D modela
- ezdxf za izvoz 2D linija u CAD (DXF)
5. Zaključak
Kombinacija Fibonacijeve distribucije i KD stabla daje nam snažan metod za konstrukciju efikasne 3D mreže koja ima primenu u kompjuterskoj grafici, analizi podataka, geodeziji i modelovanju geodetskih kupola.
Matematički, ovaj zadatak se zasniva na efikasnoj upotrebi Fibonacci rasporeda za ravnomerno raspoređivanje tačaka na sferi, KDTree za brzo pronalaženje najbližih suseda, i korišćenju cilindara za stvaranje 3D modela. Ovo je optimalno za izvoz u formate kao što su DXF i STL za vizualizaciju 3D mreže.
Za ovaj program biće potrebno da instalirate sledeće Python biblioteke:
- NumPy — Za rad sa numeričkim podacima i vektorima.
- SciPy — Za KDTree pretragu najbližih suseda.
- Meshio — Za izvoz u PLY format.
- Trimesh — Za kreiranje 3D modela i rad sa cilindrima u STL formatu.
- ezdxf — Za izvoz u DXF format.
Komandna linija za instalaciju svih potrebnih biblioteka putem pip menadžera paketa je:
pip install numpy scipy meshio trimesh ezdxfObjašnjenje:
- NumPy je osnova za rad sa nizovima, vektorima i matrica.
- SciPy se koristi za KDTree pretragu najbližih suseda, koja je ključna za brzo pretrživanje tačaka u 3D prostoru.
- Meshio omogućava čitanje i pisanje 3D formata kao što je PLY.
- Trimesh se koristi za rad sa 3D geometrijama, uključujući kreiranje cilindra i manipulaciju modelima u STL formatu.
- ezdxf omogućava rad sa DXF fajlovima, standardnim formatom za 2D i 3D CAD podatke.
Jednom kada instalirate ove biblioteke, vaš program bi trebao raditi bez problema.
Programski kod u python3 za 777 tačaka:
import numpy as np
from scipy.spatial import KDTree
import trimesh
import os
import ezdxf
# 1. Generisanje tačaka na sferi pomoću Fibonacci algoritma
n = 777
indices = np.arange(0, n) + 0.5
phi = np.arccos(1 - 2 * indices / n)
theta = np.pi * (1 + 5**0.5) * indices
x = np.cos(theta) * np.sin(phi)
y = np.sin(theta) * np.sin(phi)
z = np.cos(phi)
points = np.vstack((x, y, z)).T
# 2. Nađi 6 najbližih suseda za svaku tačku
tree = KDTree(points)
k = 6
edges = set()
for i, p in enumerate(points):
_, idxs = tree.query(p, k=k+1)
for j in idxs[1:]: # preskoči sebe
edge = tuple(sorted((i, j)))
edges.add(edge)
edges_array = np.array(list(edges))
# 3. Kreiraj izlazni direktorijum
output_dir = "sfera_izvoz_kdtree"
os.makedirs(output_dir, exist_ok=True)
# 4. Sačuvaj DXF fajl (linije) koristeći ezdxf
def save_dxf(filename, points, edges):
doc = ezdxf.new()
msp = doc.modelspace()
# Dodaj linije
for i, j in edges:
start = points[i]
end = points[j]
msp.add_line(start, end, dxfattribs={'layer': 'lines'})
doc.saveas(filename)
# Pozovi funkciju za DXF
save_dxf(os.path.join(output_dir, "mreza_kdtree.dxf"), points, edges_array)
# 5. STL izvoz: šipke kao tanki cilindri
cylinder_radius = 0.005
cylinders = []
for i, j in edges_array:
start = points[i]
end = points[j]
vec = end - start
length = np.linalg.norm(vec)
if length == 0:
continue
direction = vec / length
cyl = trimesh.creation.cylinder(radius=cylinder_radius, height=length, sections=6)
T = trimesh.geometry.align_vectors([0, 0, 1], direction)
cyl.apply_transform(T)
cyl.apply_translation((start + end) / 2)
cylinders.append(cyl)
# Kombinuj sve cilindre u jedan mesh i sačuvaj STL
combined = trimesh.util.concatenate(cylinders)
combined.export(os.path.join(output_dir, "mreza_kdtree.stl"))
Fibonacijeva distribucija tačaka na sferi
Fibonacijeva distribucija koristi zlatni ugao da rasporedi tačke što ravnomernije po površini sfere. Ovaj pristup je inspirisan prirodnim obrascima kao što su raspored semena u suncokretu ili listova na biljci.
1. Zlatni ugao
Zlatni ugao izražava se u radijanima kao:
\[ \theta_g = \pi (3 – \sqrt{5}) \approx 2.39996 \]
2. Koordinate tačaka
Za broj tačaka \( n \), i svaku tačku indeksa \( i \in \{0, 1, \dots, n-1\} \), računamo:
\[ k = i + 0.5 \] \[ \phi_i = \arccos\left(1 – \frac{2k}{n}\right) \] \[ \theta_i = \theta_g \cdot k \]
Tada su kartezijanske koordinate tačke na jedinicnoj sferi:
\[ x_i = \cos(\theta_i) \cdot \sin(\phi_i) \] \[ y_i = \sin(\theta_i) \cdot \sin(\phi_i) \] \[ z_i = \cos(\phi_i) \]
3. Vizuelizacija i prednosti
Ovaj metod daje spiralni raspored tačaka od severnog do južnog pola, sa jednakim rastojanjem po visini (z-osi) i rotacijom od zlatnog ugla u horizontalnoj ravni.
- Bez klasterizacije na polovima
- Bez optimizacija ili numeričkih iteracija
- Odlična aproksimacija ravnomerne distribucije
KD stablo (k-dimensional tree)
KD stablo je binarno stablo koje organizuje tačke u \( \mathbb{R}^k \). Namenjeno je efikasnim prostornim pretragama kao što su pronalaženje najbližeg suseda, pretraga u opsegu i klasifikacija.
1. Formalna definicija
Neka je \( P = \{p_1, p_2, \dots, p_n\} \subset \mathbb{R}^k \) skup tačaka. KD stablo je binarno stablo koje rekurzivno deli prostor duž dimenzija \( 0, 1, \dots, k-1 \) redom.
Svaki čvor u stablu sadrži:
- tačku \( p_i \in \mathbb{R}^k \)
- indeks dimenzije \( d \in \{0, \dots, k-1\} \)
- levog i desnog potomka: tačke manje ili veće u toj dimenziji
2. Algoritam konstrukcije
Za skup \( P \) i trenutnu dubinu \( depth \), dimenzija za podelu je:
\[ d = depth \bmod k \]
Koraci:
- Sortiraj tačke po dimenziji \( d \)
- Izaberi medianu \( m \) kao koren
- Levo podstablo gradi od tačaka manjih od \( m \) u dimenziji \( d \)
- Desno podstablo gradi od tačaka većih od \( m \) u dimenziji \( d \)
- Ponavljaj rekurzivno
3. Pronalazak najbližeg suseda
Cilj je pronaći tačku \( p^* \in P \) koja minimizuje rastojanje do zadate tačke \( q \in \mathbb{R}^k \):
\[ p^* = \arg\min_{p \in P} \|p – q\|_2 \]
Pretraga koristi rekurzivno spuštanje i vraćanje (backtracking), uz mogućnost orezivanja grana koje ne mogu sadržati bližeg kandidata od trenutno najboljeg.
4. Prednosti i složenost
- Vreme konstrukcije: \( \mathcal{O}(n \log n) \)
- Pretraga najbližeg suseda: prosečno \( \mathcal{O}(\log n) \), ali može biti i linearno u najgorem slučaju
- Efikasan za male dimenzije (do 20), ali manje pogodan za visoke dimenzije (tzv. “prokletstvo dimenzionalnosti”)
5. Vizuelna intuicija (za 2D)
U 2D prostoru, prvo delimo prostor vertikalnom linijom (npr. po x-osi), zatim horizontalnom (po y-osi), pa opet po x-osi, itd. Tako se prostor rekurzivno deli na sve manje regione koji sadrže tačke.
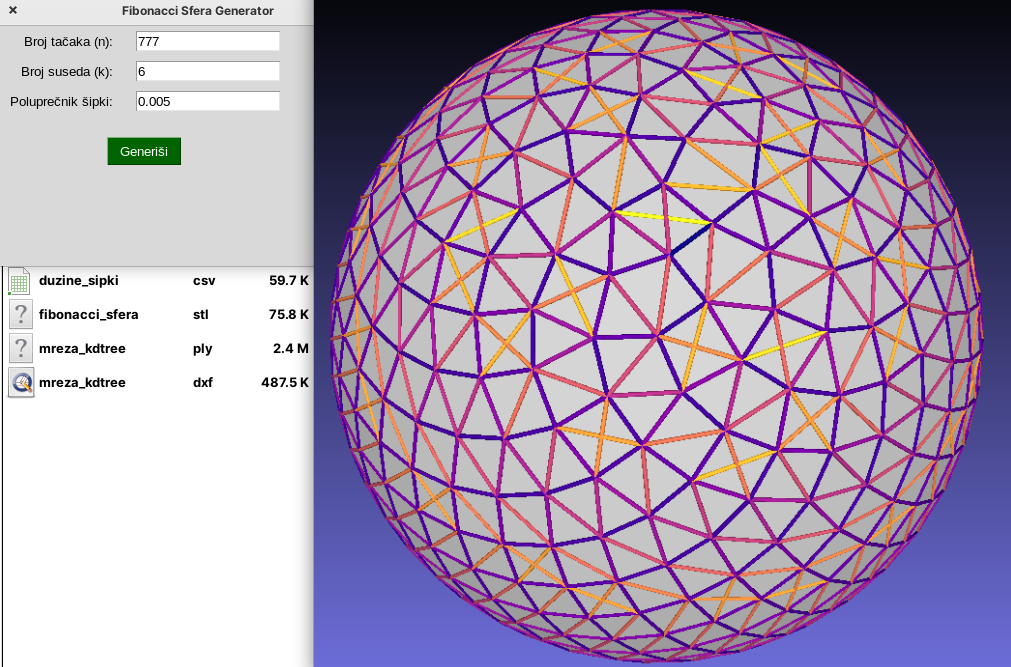
GUI verzija programa:
import tkinter as tk
from tkinter import filedialog, messagebox
import numpy as np
from scipy.spatial import KDTree, ConvexHull
import trimesh
import trimesh.repair
import os
import csv
from matplotlib import cm
import ezdxf
# Generisanje Fibonacci sfere
def generate_fibonacci_sphere(n):
indices = np.arange(0, n) + 0.5
phi = np.arccos(1 - 2 * indices / n)
theta = np.pi * (1 + 5 ** 0.5) * indices
x = np.cos(theta) * np.sin(phi)
y = np.sin(theta) * np.sin(phi)
z = np.cos(phi)
return np.vstack((x, y, z)).T
# Pronalazak ivica preko KD stabla
def find_edges(points, k):
tree = KDTree(points)
edges = set()
for i, p in enumerate(points):
_, idxs = tree.query(p, k=k + 1)
for j in idxs[1:]:
edge = tuple(sorted((i, j)))
edges.add(edge)
return np.array(list(edges))
# Bojenje po dužini
def color_from_length(lengths, cmap=cm.plasma):
norm = (lengths - lengths.min()) / (lengths.max() - lengths.min())
colors = (cmap(norm)[:, :3] * 255).astype(np.uint8)
return colors
# Čuvanje CSV izveštaja
def save_csv(filename, lengths):
stats = {
'min': np.min(lengths),
'max': np.max(lengths),
'mean': np.mean(lengths),
'std': np.std(lengths),
'count': len(lengths)
}
with open(filename, 'w', newline='') as f:
writer = csv.writer(f)
writer.writerow(['index', 'length'])
for i, l in enumerate(lengths):
writer.writerow([i, l])
writer.writerow([])
writer.writerow(['stat', 'value'])
for k, v in stats.items():
writer.writerow([k, v])
# Čuvanje DXF fajla
def save_dxf(filename, points, edges):
doc = ezdxf.new()
msp = doc.modelspace()
for i, j in edges:
msp.add_line(points[i], points[j])
doc.saveas(filename)
# Čuvanje PLY fajla sa obojenim cilindrima
def save_ply(filename, edges, points, colors, radius):
cylinders = []
for (i, j), color in zip(edges, colors):
start = points[i]
end = points[j]
vec = end - start
length = np.linalg.norm(vec)
if length == 0:
continue
direction = vec / length
cyl = trimesh.creation.cylinder(radius=radius, height=length, sections=12)
T = trimesh.geometry.align_vectors([0, 0, 1], direction)
cyl.apply_transform(T)
cyl.apply_translation((start + end) / 2)
cyl.visual.vertex_colors = np.tile(color, (len(cyl.vertices), 1))
cylinders.append(cyl)
combined = trimesh.util.concatenate(cylinders)
combined.export(filename)
# Čuvanje STL fajla sa trouglovima (sfera)
def save_stl_convex(filename, points):
hull = ConvexHull(points)
mesh = trimesh.Trimesh(vertices=points, faces=hull.simplices, process=True)
mesh.remove_duplicate_faces()
mesh.remove_unreferenced_vertices()
mesh.fix_normals()
trimesh.repair.fix_winding(mesh)
mesh.export(filename)
# GUI funkcija
def run_generation():
try:
n = int(entry_n.get())
k = int(entry_k.get())
radius = float(entry_radius.get())
output_dir = filedialog.askdirectory(title="Izaberi izlazni direktorijum")
if not output_dir:
return
points = generate_fibonacci_sphere(n)
edges = find_edges(points, k)
lengths = np.linalg.norm(points[edges[:, 0]] - points[edges[:, 1]], axis=1)
colors = color_from_length(lengths)
save_dxf(os.path.join(output_dir, "mreza_kdtree.dxf"), points, edges)
save_ply(os.path.join(output_dir, "mreza_kdtree.ply"), edges, points, colors, radius)
save_csv(os.path.join(output_dir, "duzine_sipki.csv"), lengths)
save_stl_convex(os.path.join(output_dir, "fibonacci_sfera.stl"), points)
messagebox.showinfo("Uspeh", "Fajlovi su uspešno generisani!")
except Exception as e:
messagebox.showerror("Greška", str(e))
# GUI
root = tk.Tk()
root.title("Fibonacci Sfera Generator")
root.geometry("400x240")
root.resizable(False, False)
tk.Label(root, text="Broj tačaka (n):").grid(row=0, column=0, sticky="e", padx=10, pady=5)
entry_n = tk.Entry(root)
entry_n.insert(0, "777")
entry_n.grid(row=0, column=1, padx=10)
tk.Label(root, text="Broj suseda (k):").grid(row=1, column=0, sticky="e", padx=10, pady=5)
entry_k = tk.Entry(root)
entry_k.insert(0, "6")
entry_k.grid(row=1, column=1, padx=10)
tk.Label(root, text="Poluprečnik šipki:").grid(row=2, column=0, sticky="e", padx=10, pady=5)
entry_radius = tk.Entry(root)
entry_radius.insert(0, "0.005")
entry_radius.grid(row=2, column=1, padx=10)
btn_generate = tk.Button(root, text="Generiši", command=run_generation, bg="darkgreen", fg="white")
btn_generate.grid(row=4, column=0, columnspan=2, pady=20)
root.mainloop()
